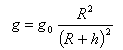|
exercice
1
|
champ
à une altitude donnée
|
|
La trajectoire d'un satellite est
elliptique. Son apogée a une altitude de
2967 km par rapport à la terre. So
périgé a une altitude de 806 km. Le
rayon terrestre est de 6380 km. Le champ de
gravitation au sol est 9,8 ms-2. La
valeur du champ de gravitation crée par la
terre au point d'apogée est de :
4,56 Nkg-1 ; 2,28 N kg-1 ;
0,228 ms-2 ; 9,8 ms-2
(choisir la bonne
réponse)
corrigé
|
|
R+h=9347 km ; 6380/9347= 0,682 ;
0,682*0,682*9,8
a=4,56
ms-2 ou
Nkg-1
|
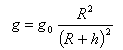
|
|
|
|
exercice
2
|
équigravité
: champ nul entre la terre et la lune
?
|
|
soit ML et
MT les masses de la lune et de la terre,
MT = 81
ML
soit RL et
RT leurs rayons RT =3,66
RL
il existe sur la
ligne joignant les centres des 2 astres un point M
où les champs de gravitation sont egaux. il
faut situer ce point en calculant sa distance d au
centre de la terre.
distance des centres
des 2 astres D=3,8 108 m.
corrigé
|
|
Le point
cherché se trouve à la distance
d
de la Terre et ( D-d
) de la Lune
.
En ce point le champ
gravitationnel créé par la Terre est
g1 =
GMT /
d²=G*81ML/d²
Celui créé
par la Lune est g2 =
GML / ( D-d
)²
Les deux champs sont
égaux : après division par
GML:
81/d² =
1 / ( D-d )²
Il ne reste plus
qu'à résoudre l'équation du 2e
degré ainsi obtenue.
9²*(
D-d )²=d² ou
9²*(
D-d )²-d²=0
différence
de deux carrés
d'où d=0,9
D=3,42
108 m
|
|
|
|
exercice
3
|
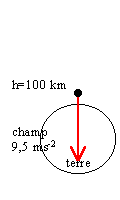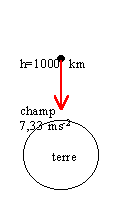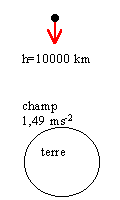
champ
de
gravitation à l'intérieur de la
terre
|
|
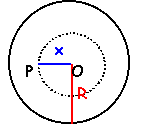
La terre est un corps à symètrie
sphérique. Comment calculer le champ de
gravitation en un point P tel que OP=x ?
P est à
l'extérieur de la terre; on concentre la
masse de la terre en son centre.
P est à
l'intérieur de la terre; seules les masses
contenues dans la sphère de rayon OP jouent
un rôle sur le champ en P. Ces masses peuvent
être concentrées au centre de la
terre.
RT=6400 km;
g=9,81 m s-2; G=6,67 10-11
SI
- Calculer la masse de la terre.
- Calculer la masse volumique de la
terre.
- Dans un puits imaginaire,
percè jusqu'au centre de la terre, on
place un objet de masse m. Exprimer en fonction
de R, x,m le poids de cet objet.
- Que vaut ce poids au centre de la
terre.
|
corrigé
|
|
champ gravitation au
sol(m
s-2) = G
*Masse terre
divisée par rayon terre ²
(m²)
9,81=6,67 10-11
MT/6,4² 1012
MT=6
1024 kg
volume d'une sphère 4/3 p
rayon3
4/3*3,14*6,43
1018 =1,1 1021
m3
masse volumique kg
m-3
= masse kg
divisée par volume
m3
6
1024
/1,1 1021 =5454
kg
m-3
masse à prendre en compte
: volume fois masse volumique
volume sphère de
rayon x:
4/3*p*
x3
masse volumique terre:
MT/ ( 4/3 p
rayon3)
masse à prendre en
compte :
MT*
x3
/
rayon3
poids de l'objet de masse
m : m*MT*
x3
/
rayon3
Au centre de la terre x=0
et le poids de cet objet est nul.
( sa masse n'a pas
changée)
|
|
exercice
4
|
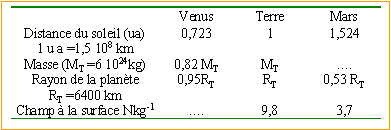
quelques
satellites du soleil
|
- Comparer la valeur du champ de gravitation
à la surface de Vénus à
celui à la surface de la terre.
- Comparer la valeur de la masse de Mars
à celle de la Terre.
- La recherche de vie sur MARS a
été confiée à des
sondes Viking .Parmi les propositions suivantes
cochez la bonne réponse:
- Lorsqu'une sonde Viking est à
égale distance de la Terre et de Mars les
champs de gravitation
gT de la terre et gM
de Mars à la distance z vérifient la
relation
gT = gM ;
gM = 1,524 gT ; gM
= 0,11 gT
- Le poids d'une sonde Viking à la
surface de la Terre Pterre et
à la surface de Mars PMars
vérifient
la relation
PMars = 0 ,11 Pterre ;
Pterre = 2,64 PMars ;
PMars = 0,38 Pterre ;
Pterre = PMars
- La masse d'une sonde Viking est
la même sur Terre et sur Mars - plus
grande sur Terre que sur Mars - plus petite sur
Terre que sur Mars
- Il existe entre Mars et la Terre un point M
où les champs de gravitation martien et
terrestre se
compensent
M est équidistant des 2 planètes -
M plus proche de Mars - M plus proche de la
Terre
corrigé
|
|
champ de gravitation à la surface de
:
la terre : GMT / RT²=
9,8 N kg-1.
Vénus : GMT*0,82 / ( 0,95
RT)² = GMT /
RT²*0,82/ 0,95² = 0,91*9,8 =
8,9 N kg-1.
terre : GMT = 9,8
RT²
Mars: GMm=3,7 ( 0,53
RT)²
Mm /MT = 3,7*0,53² /
9,8 = 0,106
champ crée par la terre à la distance
d : gT= 9,8 R²T /
d²
champ crée par mars à la distance
d : gM= 3,7 (0,53 RT)² /
d² = 3,7*0,53²RT² /
d²
gT / gM= 9,8 /
(3,7*0,53²) = 9,42
gM= 0,106 gT
poids (N)= masse (kg)fois
accélération de la pesanteur(N
kg-1).
Le rapport des poids est égal au rapport
des accélérations 9,8 /3,7 = 2,65
Poids (terre) = 2,65 * Poids (mars)
Par contre la masse reste constante quel que
soit le lieu.
Le point d'équigravité est plus
proche de Mars la planète la moins
massive.
retour
- menu
|
|
|
![]()
![]()