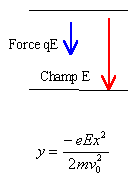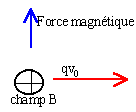|
exercice
1
|
particule
déviée par un champ
magnétique
|
|
Dans un accélérateur de particule,
des ions He2+, de masse m=6,64
10-27 kg, sont
accélérés jusqu'à une
vitesse de 1,25 107 ms-1. Ils
pénètrent alors dans une
région où règne un champ
magnétique d'intensité B=1,3T, de
direction perpendiculaire à leur vitesse
.charge
élémentaire e=1,6 10-19
C.
l'intensité de la
force magnétique s'exerçant sur les
ions est : 5,2 mN ; 5,2 10-10 N ;2,6
10 -10 N ; 5,2pN ; 5,2
mN
|
|
|
corrigé
|
|
|
valeur de la force
2evB
|
5,2
10-12 N
5,2
pN
|
|
|
|
exercice
2
|
champ
magnétique - force de
Lorentz
|
|
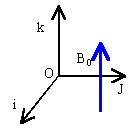
Des ions lourds, positifs, de masse
m1 et de charge q , animés
d'une vitesse v0 pénètrent
en O dans une zone où existe un champ
magnétique uniforme B0.
q=2e ; e=1,6
10-19 C ; m1= 6,4
10-26 kg ; v0= 107
ms-1 ; B=2 T
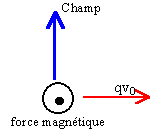
- si la vitesse est
colinéaire au vecteur unitaire k, les
ions sont
accélérés.
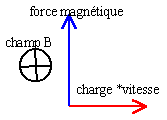
- si la vitesse est
colinéaire au vecteur unitaire j, les
ions sont déviés vers le demi axe
Ox. (vecteur unitaire i.)
- si la vitesse est
colinéaire au vecteur unitaire j, les
ions sont déviés vers le demi axe
Ox. (vecteur unitaire i .) Le point d'impact
O1 est tel que OO1=10
cm.
- Des ions de masse
m2, pénétrant en O ,
avec la même vitesse v0
dirigée suivant j, auraient la même
période de révolution que les ions
précédents de masse
m1.
|
|
|
|
corrigé
|
|
|
|
|
faux
si la vitesse et le champ magnétique sont
colinéaire , la force magnétique est
nulle et les ions ne sont ni
accélérés ni
déviés.
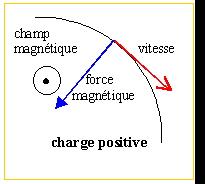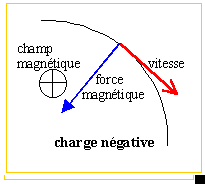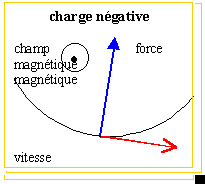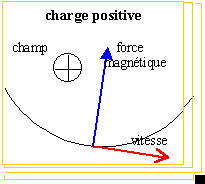
vrai
(voir schéma) la force
magnétique est colinéaire et de
même sens que le vecteur unitaire i
faux
les ions décrivent un cercle de
diamètre OO1= 0,1 le rayon doit
être égal à
mv0 /(qB0)
rayon =6,4
10-26 *107 / (3,2
10-19
*2)= 1
mètre
faux
la circonférence (2p
r ) est parcourue à la vitesse v0
de valeur constante pendant une durée
T
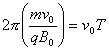 la
durée dépend de la
masse la
durée dépend de la
masse
|
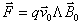
|
|
|
|
|
exercice
3
|
proton
dans des champs électriques et
magnétiques
|
|
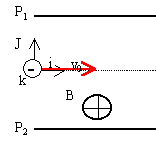
On considére deux plaques P1
et P2 de longueur l=20 cm et distantes
de d=10 cm.On étudie le mouvement d'un
proton se déplaçant dans la zone
centrale. Le proton arrive en O avec une vitesse
v0=106 ms-1.
q=1,6 10-19 C.
masse du proton m=1,67 10-27 kg. B=50
mT
- On établit
entre les plaques un tension
UP1P2=200V ; le proton va subir une
déflexion circulaire vers le
haut.
- Le proton sort de cet
espace en un point S tel que S( 0,2 m ; -0,004
m)
- Entre les plaques la
tension est supprimée, mais il
règne maintenant un champ
magnétique uniforme B colinéaire
au vecteur unitaire k mais de sens contraire. Le
proton va subir une déflexion circulaire
vers le haut.
- Dans les conditions
précédentes, la trajectoire du
proton est pratiquement confondue avec l'axe de
vecteur unitaire i
|
|
|
|
|
corrigé
|
|
|
|
|
faux
le proton subit une déflexion
vers le bas. La
trajectoire n'est pas circulaire, il s'agit d'un
arc de parabole
vrai
remplacer dans
l'expression de y les lettres par leurs
valeurs.(E=200 /
0,1) y=- 4
mm
la troisième
proposition est vraie
voir schéma
vrai
le rayon de l'arc de cercle est de 10 m ; cet arc
de cercle est pratiquement confondu avec
l'horizontale dans l'espace de longueur 0,2 m entre
les plaques
r=1,66
10-27*106 /(1,6
10-19
*0,05)=10m
|
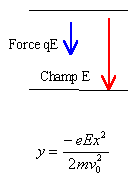
|
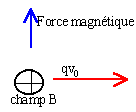
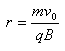
|
|
|
|
exercice
4
|
cyclotron
|
|
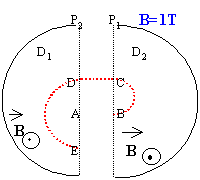
Un cyclotron est un
accélérateur de particules. Dans les
2 demi disques règne un champ
magnétique B uniforme. Entre les grilles
P1 et P2 règne un
champ électrique crée par une tension
sinusoidale d'amplitude 1000V. En A on injecte un
proton de charge e, de masse m, sans vitesse
initiale.
e=1,6 10-19 C;
m=1,67 10-27 kg
- Quelle est la vitesse
du proton en B ?
- Quel est le rayon du
demi cercle BC ?
- Quelle est la
durée du parcours BC
En déduire la
fréquence de la tension
alternative.
|
|
|
|
corrigé
|
|
|
|
|
A
chaque passage entre les demi disques le proton est
accéléré par le champ
électrique.
Son énergie cinétique augmente de
la quantité : eU
U étant l'amplitude
de la tension sinusoidale.
vitesse
en B: 0,5 mv²B=eU
;
v²B=2eU/m
vB=4,38
105 m s-1
rayon
de l'arc de cercle
r=mvB/(eB)
r=4,57 mm
L'arc de cercle
BCde longueur
p
r
est parcouru à
vitesse constante vB.
La durée du
parcours est :
p
r/
vB=p
m/(eB)
durée
indépendante de la vitesse
3,27
10-8 s
Le proton doit
être accéléré à
chaque passage entre les disques:
pour
cela:la tension
sinusoidale doit atteindre son amplitude (valeur
maxi)
et la tension
sinusoidale doit changer de signe.
La durée de
parcours dans chaque demi disque doit être
égale à une demi période de la
tension sinusoidale.
période:2*3,27
10-8 s
fréquence
:1/période=1,53
107
Hz
|

|
retour
- menu
|
![]()

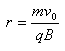


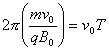 la
durée dépend de la
masse
la
durée dépend de la
masse