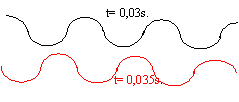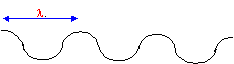|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. ..
.. célérité dans les liquides ; caténaire ; dispersion ; diffraction .... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
célérité dans les liquides : Un émetteur et un récepteur d'ultrasons sont fixés sur deux couvercles vissés aux deux extrémités d'un tube étanche, rempli d'eau. La distance "émetteur-récepteur" est notée D=0,9 m. On donne les oscillogrammes( correspondant à la même salve) des tensions émises et reçues. 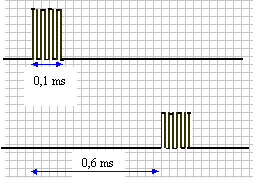
corrigé 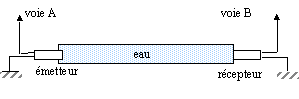
4 périodes correspondent à 0,1 ms ; T = 10-4 / 4 = 2,5 10-5 s la fréquence est l'inverse de la période : f = 1/ 2,5 10-5 = 40 000 Hz. la célérité (m/s) est égale à la distance D(m) divisée par le décalage Dt (s) : 0,9 / 6 10-4 = 1500 m/s. pour l'acétone : V = 0,9 / 7,6 10-4 = 1184 m/s. pour le glycérol : V = 0,9 / 4,7 10-4 = 1915 m/s. pour le kérosène : V= 0,9 / 6,8 10-4 = 1324 m/s. pour l'air : Dt = 0,9 / 341 = 2,63 ms.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
catènaire :
corrigé On appelle onde mécanique le phénomène de propagation d'une perturbation dans un milieu élastique, sans transport de matière ; cette onde transorte de l'énergie. Une onde est transversale si la perturbation provoquée est perpendiculaire à la direction de propagation . V = racine carée ( F / m ) volume de la corde : p r2 L = 3,14 * (5 10-4)2 *0,42= 3,3 10-7 m3. masse de la corde : volume (m3) fois masse volumique (kg/m3) = 3,3 10-7 * 7,86 103 = 2,6 10-3 kg. masse linéique m = 2,6 10-3 / 0,42 = 6,17 10-3 kg/m. célérité V1 = [843 / 6,17 10-3 ]0,5 = 369,6 m/s. célérité V2 = [2,6 104 / 1,4 ]0,5 = 136,3 m/s. vitesse limite de la rame : 136,3 *0,7 = 95,4 m/s soit 95,4*3,6 = 343,5 km/h. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
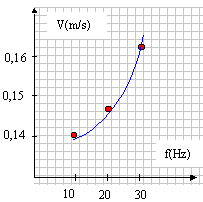
Dispersion des ondes à la surface de l'eau : Des ondes rectilignes sinusoïdales sont crées à la surface d'une cuve à ondes. Un bouton de réglage permet de faire varier la fréquence de ces ondes. Afin de mesurer les longueur d'ondes on utilise un éclairage stroboscopique, qui stabilise l'image. Pour chaque fréquence, on mesure sir l'écran, la distance D séparant dix franges brillantes consécutives. Le grandissemnt de l'image formée sur l'écran est g = 1,79.
corrigé la distance séparant deux franges brillantes consécutives est égale à la longueur d'onde l . tenir compte du grandissement : 10 l = D / g soit l = 0,1 D / g . la célérité V (m/s) est égale à la longueur d'onde (m) fois la fréquence (Hz) : V = l f = 0,1 D f / g .
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
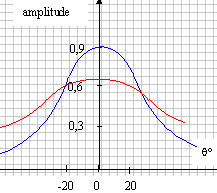
diffraction des ultrasons : Un émetteur émet en continu des ultrasons de fréquence f= 40 kHz. A 15 cm de ce dernier, un récepteur placé dans une gouttière en forme d'arc de cercle reçoit ces ondes. Ce récepteur est relié à un oscilloscope ( sensibilité étant 5 ms / div).On relève l'amplitude de l'onde reçue en fonction de l'angle q que fait l'axe de symétrie du système avec la droite joignant l'émetteur au récepteur.(figure (1) 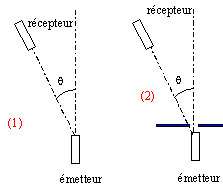 On obtient les valeurs suivantes :
corrigé 
la longueur d'onde l (m) est égale à la célérité (m/s) divisée par la fréquence (Hz) l = 339 / 40 000 = 8,47 mm.
l'onde ultrasonore subit un phénomène de diffraction en passant patr l'ouverture : la dimention de cette fente est du même ordre de grandeur que de la longueur d'onde de l'onde. L'amplitude des ultrasons reçus est moins grande mais plus étalée dans l'espace
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
chute dans l'eau : Une petite bille tombe dans une cuvette cylindrique remplie d'eau de rayon 60 cm. La bille est initialement à 80 cm au dessus de la surface de l'eau. On néglige les frottements de l'air. L'origine des temps est prise à l'instant du contact avec l'eau. Le niveau de référence pour l'énergie potentielle est la surface de l'eau. Le rayon de la bille est de 5,00 mm et sa masse volumique est r=2,0 103 kg/m3 ; on prendra g=9,8N/kg ; le volume de la sphère : V=4/3 p R3.
corrigé volume de la bille : 4*3,14/3 (5 10-3)3 = 5,23 10-7 m3. masse de la bille :5,23 10-7 *2 103 = 10,46 10-4 kg = 1,05 g. l'énergie potentielle de pesanteur initiale est convertie en énergie cinétique au cours de la chute. En absence de frottements l'énergie mécanique se conserve. mgh = ½mv² d'où v² = 2gh = 2*9,8*0,8 = 15,68 soit v = 3,96 m/s. l'énergie cinétique perdue par la bille au cours du choc est transférée au milieu liquide : on observe des ondes progressives transversales( rides circulaires) à la surface de l'eau se propageant dans toutes les directions à partir du point d'impact. La bille tombe au centre de la cuvette : l'onde parcourt 0,6 m en 0,1 s ; la vitesse de propagation est : v = 0,6 / 0,1 = 6 m/s. si h = 50 cm, l'énergie cinétique de la bille juste avant l'impact est moindre et l'énergie transférée au milieu liquide est plus petite: mais la célérité de l'onde ne change pas. L'inertie d'un milieu est mesurée par sa masse volumique : la célérité d'une onde décroît avec l'inertie mais par contre croît avec la rigidité du milieu si la rigidité de l'eau et de l'huile est identique, alors la célérité est plus faible dans l'huile. le bouchon reproduit le mouvement de la source avec le retard t= x/v = 0,01 /6 = 1,66 10-3 s. le bouchon peut récupérer au maximum la moitié de l'énergie cinétique. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
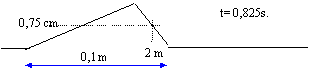
sur une corde : On déplace
verticalement l'extrémité S d'une longue corde tendue, horizontale.
L'élongation ys du point S atteint sa valeur maximale à la
date t=30 ms et ses variations en fonction du temps sont données dans
le tableau ci-dessous.
corrigé 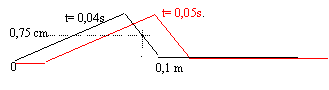
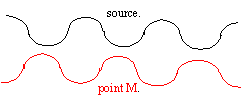
en noir aspect de la corde à la date t = 0,04s ; en rouge aspect de la corde à la date t = 0,05s. à la date t = 5ms, l'élongation y= 0,75 cm pour la première fois; le point M reproduit le mouvement de la source avec le retard t = SM/v = 0,825-0,05 = 0,82 s v= 2/0,82 = 2,44 m/s. longueur de la portion de corde affectée par la déformation à t >0,04 s : 2,44*0,04 = 0,0976 m environ 0,1 m. M reçoit le signal à la date t = 0,82 s et se retrouve au repos 0,04 s plus tard. soit P le point d'élongation maximale; P est situé avant M. Il s'écoule 10 ms entre l'instant où yP est maximale et l'insatnt où M reçoit le signal. alors SP = 2,44 * 0,810=1,976 m
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
corrigé la vitesse de la lumière de l'éclair est très supérieure à la vitesse du son dans l'air . 340 * 3 = 1020 m
et 340*4,5 = 1530 m l'orage s'éloigne
30 / 1500 = 0,02 s ( dans l'eau) total : 0,149s.
le son se propage dans l'acier est est perçu à la date : 100/v = 0,2941-0,277 = 0,0171 s vitesse du son dans l'acier : 100 / 0,0171 = 5848 m/s.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Aspect d'une corde vibrante Un vibreur impose à une corde de 30 cm de long, une perturbation sinusoïdale de période T=0,01s. La célérité v des ondes mécaniques le long de la corde est de 10 m/s et l'amplitude maximale y0 de la perturbation est de 1 cm. On néglige dans tout l'exercice l'effet de la pesanteur.
corrigé fréquence f = 100 Hz ; pulsation w= 2*3,14*100 = 628 rad/s ; amplitude y0 = 0,01 m yS = 0,01 cos(628t) retard de M : t = x/v M reproduit le mouvement de la source avec le retard t soit yM=0,01 cos(628(t-x/v)).
si x = 0,15 m , le retard t vaut 0,15/10 = 0,015s soit 1,5 périodes yM=0,01 cos(628(t-0,015)). la source et le point M sont séparés par un nombre impair de demi période : ils sont en opposition de phase.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Observation stroboscopique d'une corde Un vibreur provoque une onde périodique sinusoïdale transversale, de fréquence N=200 Hz et se propageant le long d'une corde à vitesse v=40 m/s. Il n'y a pas d'onde de retour - menu (ou onde réfléchie). On observe le phénomène sous l'éclairage d'un stroboscope.
corrigé période temporelle T=1/200 =0,005 s ; période spatiale : l = vT =40*0,005 =0,2 m. l'immobilité apparente est obtenue lorsque la fréquence des éclairs est un multiple de la fréquence de l'onde Ne = 200 k avec k entier
distance réelle parcourue par l'onde entre deux éclairs consécutifs : durée entre deux éclairs : Dt = 1/198 s ; v = 40 m/s d'où d = 40/198 =0,202 m. c'est à dire l + 0,002 = l + 0,01 l . l'observateur voit l'onde progresser l'onde de 0,01 l soit 0,002 m entre deux éclairs c'est à dire en 1/198s vitesse apparente de l'onde : 0,002*198 = 0,4 m/s si la fréquence des éclairs est 202Hz, on observe un déplacement apparent identique au précédent mais en sens contraire du déplacement réel de l'onde.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ondes sonores dans l'air : Deux petits microphones M1 et M2 séparés d'une distance d sont disposés sur l'axe de symétrie d'un haut parleur produisant une onde sonore sinusoïdale de fréquence N réglable. Ils sont reliés respectivement aux voies 1 et 2 d'un oscilloscope, de même sensibilité verticale.On fixe d=34cm et N=2000Hz.
corrigé période des ondes : 1/2000 = 0,5 ms. deux périodes doivent être visibles ( soit 1 ms) sur 10 divisions : sensibilité 0,1 ms / div. le micro M2 est plus éloigné de la source que M1 : l'onde sonore perd de l'énergie au fur et à mesure que l'on s'éloigne de la source. L'amplitude sur la voie 2 de l'oscilloscope sera donc plus faible que sur la voie 1. La célérité du son dans l'air est 340 m/s; la fréquence des ondes est 2000 Hz : la longueur d'onde est alors : l = 340/2000 =0,17 m les deux
microphones sont séparés par un nombre entier de longueur d'onde : on
observe donc deux sinusoïdes en phase (non décalées l'une par rapport à
l'autre).
la longueur d'onde est alors : l = 340/1000 =0,34 m les deux microphones sont séparés par une demi longueur d'onde : on observe donc deux sinusoïdes en opposition de phase Les deux courbes observées seront à nouveau en phase si les deux microphones sont distants d'une longueur d'onde soit 34 cm. retour - menu |