Mathématiques. Géométrie. Bac Asie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
Exercice 1. 5 points.
 L’espace est rapporté à un repère orthonormé . On considère :
a un réel quelconque ;
 les points A(1; 1; 0), B(2; 1; 0) et C(a ; 3 ; a) ;
  (d) la droite dont une représentation paramétrique est : x = 1+ t; y = 2t ;  z = − t , t réel.
 Pour chacune des affirmations suivantes, préciser si elle est vraie ou fausse, puis justifier la réponse donnée. Une réponse non argumentée ne sera pas prise en compte.
 Affirmation 1 : Pour toutes les valeurs de a, les points A, B et C définissent un plan et un vecteur normal à ce plan  a pour coordonnées (0 ; 1 ; 0).

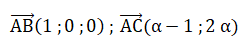
Quel que soit a, ces coordonnées ne sont pas proportionnelles ; ces vecteurs n'étant pas colinéaires, ils définissent un plan.

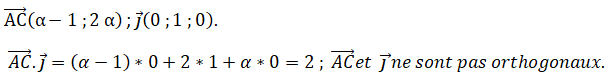Affirmation fausse.

 Affirmation 2 : Il existe exactement une valeur de a telle que les droites (AC) et (d) soient parallèles.

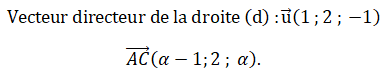
Pour que ces droites soient parallèles, il faudrait que ces deux vecteurs soient proportionnels.
Ces deux vecteurs ayant la même ordonnée 2,  ils devraient être égaux.
En choisissant a = -1 : les altitudes sont égales mais pas les abscisses.
En choisissant a = 2 : les abscisses sont égales mais pas les ordonnées.
Pour toutes autres valeurs de a, abscisses et ordonnées seront différentes.
Affirmation fausse.

  Affirmation 3 : Une mesure de l’angle OAB est 135°. 

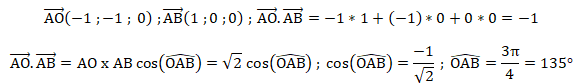Affirmation vraie.

 Affirmation 4 : Le projeté orthogonal du point A sur la droite (d) est le point H(1; 2; 2).
H appartient à la droite (d) : xH = 1+t = 1 ; donc t = 0.
Alors  yH = 2t =0, différent de 2.
Le point H n'est pas sur la droite (d). H n'est pas le projeté orthogonal de A sur la droite (d).
Affirmation fausse.

 Affirmation 5 : La sphère de centre O et de rayon 1 rencontre la droite (d) en deux points distincts. On rappelle que la sphère de centre W et de rayon r est l’ensemble des points de l’espace situés à une distance r de W.
Soit M appartenant à la droite (d) :
OM2 =(1+t)2 +(2t)2 +(1-t)2=1+2t+t2+4t2+1+t2-2t=6t2+2t+1.
OM = 1 ; OM2 = 1 : 6t2+2t+1=1 ; 6t2+2t =0 ; t = 0 et t = -1/3.
Il y a exactement deux points de la droite (d) qui sont sur la sphère.
Affirmation vraie.

... =  =
....

 L’espace est rapporté à un repère orthonormé. On considère :
 les points C(3 ; 0 ; 0), D(0 ; 2 ; 0), H(−6 ; 2 ; 2) et J( −54 / 13 ; 62 /13 ; 0) ;
le plan P d’équation cartésienne 2x +3y +6z −6 = 0;
 le plan P ′ d’équation cartésienne x −2y +3z −3 = 0;
 la droite (d) dont une représentation paramétrique est :  x = −8+ 1/ 3 t ; y = −1+ 1/ 2 t; z = −4+ t , t réel.
 Pour chacune des affirmations suivantes, préciser si elle est vraie ou fausse, puis justifier la réponse donnée. Une réponse non argumentée ne sera pas prise en compte.
 Affirmation 1 : La droite (d) est orthogonale au plan P et coupe ce plan en H.

Donc (d) est normale à (P).
Si H appartient au plan (P) : 2xH +3yH +6zH −6 = 0 ; 2*(-6) +3*2+6*2-6=0 est vraie, donc H appartient au plan (P).
Si H appartient à la droite (d), il existe t réel tel que :
-6 =-8+t / 3 ; t = 6.
 2=-1+0,5t soit t = 6 ;
2=-4 +t soit t =6.
L'affirmation est vraie.

 Affirmation 2 : La mesure en degré de l’angle DCH, arrondie à 10 −1 , est 17,3° .

L'affirmation est fausse.

 Affirmation 3 : Les plans P et P ′ sont sécants et leur intersection est la droite D dont une représentation paramétrique est :  x = 3−3t ;y = 0 ; z = t , t réel.

Ces deux vecteurs ne sont pas colinéaires, donc les deux plans ne sont pas parallèles : ils sont sécants ; leur intersection est une droite.
A( 3 ; 0 ; 0) appartient à (D). ( en faisant t=0 ).
2xA +3yA +6zA −6 = 6+0+0-6=0 ; A appartient au plan (P).
xA −2A +3zA −3 = 3-0-0+3=0 ; A appartient au plan (P').
L'intersection des plans (P) et (P') est une droite contenant le point A.
B( 0 ; 0 ; 1) appartient à (D). ( en faisant t=1 ).
2xB +3yB +6zB −6 = 0+0+6-6=0 ; B appartient au plan (P).
xB −2B +3zB −3 = 0-0+3-3=0 ; B appartient au plan (P').
L'intersection des plans (P) et (P') est une droite contenant le point B.
L'affirmation est vraie.

. Affirmation 4 : Le point J est le projeté orthogonal du point H sur la droite (CD).

C(3 ; 0 ; 0)
Représentation paramétrique de la droite (CD) :  x = 3-3t ; y = 2t ; z = 0 avec t réel.
J( −54 / 13 ; 62 /13 ; 0) ;
J appartient-il à (CD) ?
yJ = 62 / 13 = 2t ; t = 31 /13.
xJ =3-3*31 / 13 =(39-93) / 13 =-54 /13. Donc J appartient à (CD).

En conséquence J est le projeté orthogonal de H sur (CD).
L'affirmation est vraie.



  
menu