Mathématiques. Probabilités. Bac
Asie 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 2. 5 points.
Une entreprise qui fabrique des jouets doit effectuer des contrôles de
conformité avant
leur commercialisation. Dans cet exercice, on s’intéresse à deux tests
effectués par l’entreprise de jouets : un test de fabrication et un
test de sécurité.
À la suite d’un grand nombre de vérifications, l’entreprise affirme que
:
95 % des jouets réussissent le test de fabrication ;
Parmi les jouets qui réussissent le test de fabrication, 98 %
réussissent le test de
sécurité ;
1 % des jouets ne réussissent aucun des deux tests.
On choisit au hasard un jouet parmi les jouets produits.
On note : F l’évènement : « le jouet réussit le test de
fabrication »;
S l’évènement : « le jouet réussit le test de sécurité ».
Partie A
1. À partir des
données de l’énoncé, donner les probabilités P(F) et P F (S).
P(F) = 0,95 ; PF (S)= 0,98.
2. a. Construire
un arbre pondéré qui illustre la situation avec les données disponibles
dans l’énoncé.
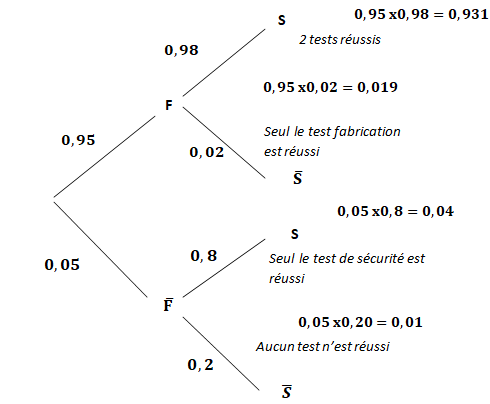 b.
b. Montrer que P non
F (non S)
= 0,2.
1 % des jouets ne réussi aucun test.
P(non F n non S) =0,01.
Pnon
F (non S)
=P(non F n non S) / P(non F) = 0,01 / 0,05 = 0,2.
3. Calculer la
probabilité que le jouet choisi réussisse les deux tests.
P(F n S) = P(F) x P F(S) = 0,95 x0,98 = 0,931.
4. Montrer que la
probabilité que le jouet réussisse le test de sécurité vaut 0,97
arrondi au centième.
Formule des probabilités totales : P(S) = P(F n S) + P(non F n S) = 0,931 +0,05 = 0,971.
5. Lorsque le jouet
a réussi le test de sécurité, quelle est la probabilité qu’il réussisse
le test de fabrication ? Donner une valeur approchée du résultat au
centième.
PS(F) = P(F n S) / P(S) = 0,931 / 0,971 = 0,9588 ~0,96.
Partie B
On prélève au hasard dans la production de l’entreprise un lot de n
jouets, où n est un
entier strictement positif. On suppose que ce prélèvement se fait sur
une quantité suffisamment grande de jouets pour être assimilé à une
succession de n tirages indépendants
avec remise.
On rappelle que la probabilité qu’un jouet réussisse le test de
fabrication est égale à 0,95.
Soit S n la variable aléatoire qui compte le nombre de jouets
ayant réussi le test de fabrication. On admet que S n suit la
loi binomiale de paramètres n et p = 0,95.
1. Exprimer
l’espérance et la variance de la variable aléatoire S n en
fonction de n.
S n suit la loi binomiale de paramètres n et p = 0,95.
E(S n) =n p = 0,95 n.
V(X) = n p (1-p) = n x0,95 x0,05 = 0,0475 n.
2. Dans cette
question, on pose n = 150.
a. Déterminer une valeur approchée à 10 −3 près de P (S 150
= 145). Interpréter
ce résultat dans le contexte de l’exercice.
P (S150
= 145)= (150 145) x0,95145 0,055=0,10884~0,109.
Dans 10,9 % des cas, 145 jouets sur 150 réussissent le test de fabrication.
b. Déterminer la
probabilité qu’au moins 94 % des jouets de ce lot réussissent le
test de fabrication. Donner une valeur approchée du résultat à 10 −3
près.
94 % des jouets sur 150 jouets du lot correspond à 150 x0,94 = 141 jouets.
P(S 150 > 141)=0,781.
3. Dans cette
question, l’entier naturel non nul n n’est plus fixé.
Soit F n la variable aléatoire définie par : F n =
S n /
n
. La variable aléatoire F n représente la proportion des
jouets qui réussissent le test de fabrication dans un lot de
n jouets prélevés.
On note E(F n) l’espérance et V (F n) la variance
de la variable aléatoire F n.
a. Montrer que E(F n)
= 0,95 et que V (F n) =
0,0475
/n
.
E(F n) = E(S n / n) =0,95 n / n = 0,95.
V(F n) =V(S n/n)=V(S n) / n 2 =0,0475 n / n 2 = 0,0475 / n.
b. On s’intéresse à
l’évènement I suivant : « la proportion de jouets qui réussissent le
test de fabrication dans un lot de n jouets est strictement comprise
entre 93 % et 97 % ».
En utilisant l’inégalité de Bienaymé-Tchebychev, déterminer une valeur
n de
la taille du lot de jouets à prélever, à partir de laquelle la
probabilité de l’évènement I est supérieure ou égale à 0,96.
0,93 < F n < 0,97 est équivalent à :
|F n-0,95| < 0,02 et P( |Fn-0,95| < 0,02) =1-P(|Fn-0,95| >0,02).
P(|Fn-0,95| >0,02) >0,96.
Or P(|Fn-E(Fn) | > t) < V(Fn) / t2.
Pour t = 0,02 : P(|Fn-0,95| >0,02)< 0,0475 / (0,022n).
475 / 4n < 0,04 ; 11875 / 4 < n ; 2968 +0,75 < n.
A partir de 2969 jouets que l'on prélève, la probabilité de l'événement I est supérieure ou égale à 0,96.
|
...
= =
|
....
|
Un test a été mis au point pour le dépistage de ce virus.
Le laboratoire fabriquant ce test fournit les caractéristiques suivantes :
- la probabilité qu’un individu atteint par le virus ait un test positif est de 0,999 ;
- la probabilité qu’un individu non atteint par le virus ait un test positif est de 0,005.
On procède à un test de dépistage systématique dans une population cible.
Un individu est choisi au hasard dans cette population. On appelle :
- M l’évènement : « l’individu choisi est atteint du chikungunya ».
- T l’évènement : « le test de l’individu choisi est positif ».
On considère que le test est fiable lorsque la probabilité qu’un individu ayant un test
positif soit atteint par le virus est supérieure à 0,95
Partie A : Étude d’un exemple
1. Donner les probabilités PM (T ) et Pnon M
(T ).
PM (T ) = 0,999 ; Pnon M
(T )=0,00.5
« En mars 2005, l’épidémie s’est propagée rapidement dans l’ile de La Réunion, avec une
flambée importante entre fin avril et début juin puis une persistance de la transmission
virale durant l’hiver austral. Au total, 270 000 personnes ont été infectées pour une population totale de 750 000 individus ».
(https://www.pasteur.fr/fr/centre-medical/fiches-maladies/chikungunya).
Fin 2005, le laboratoire a effectué un test de dépistage massif de la population de l’île de
La Réunion.
Dans cette partie, la population cible est donc la population de l’ile de La Réunion.
2. Donner la valeur exacte de P(M).
P(M = 270 000 / 750 000 =0,36.
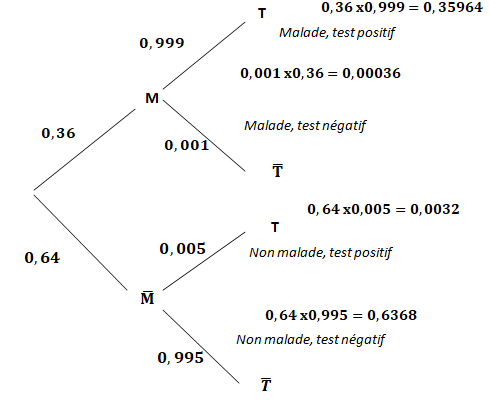
3. Recopier et compléter l’arbre pondéré donné ci-dessous.
4. Calculer la probabilité qu’un individu soit atteint par le virus et ait un test positif.
P(M n T) =P(M) x PM(T) =0,36 x0,999 = 0,35964.
5. Calculer la probabilité qu’un individu ait un test positif.
P(T) = P(M n T) + P(non M n T) = 0,35964 +0,0032=0,36384.
6. Calculer la probabilité qu’un individu ayant un test positif soit atteint par le virus.
PT(M) =P(M n T) / P(T) = 0,35964 / 0,36284 = 0,991.
7. Peut-on estimer que ce test est fiable ? Argumenter.
PT(M) > 0,95. Le test est fiable.
Partie B : Dépistage sur une population cible
Dans cette partie, on note p la proportion de personnes atteintes par le virus du chikungunya dans une population cible.
On cherche ici à tester la fiabilité du test de ce laboratoire en fonction de p.
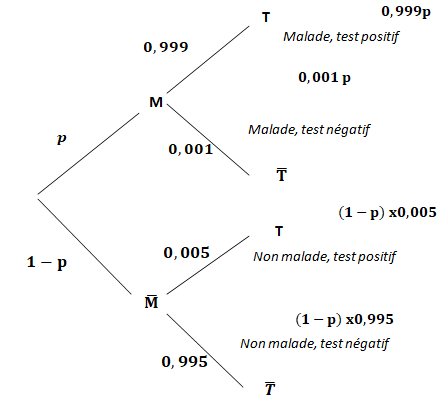
1. Recopier, en l’adaptant, l’arbre pondéré de la question A3 en tenant compte des
nouvelles données.
2. Exprimer la probabilité P(T ) en fonction de p.
P(T) = P(M n T) + P(non M n T) =0,999p +(1-p) x0,005 = 0,994 p+0,005.
3. Montrer que PT (M) =
999p/(
994p +5
).
PT (M) =P(M n T) / P(T) = 0,999p / (0,994p +0,005).
4. Pour quelles valeurs de p peut-on considérer que ce test est fiable ?
PT (M) > 0,95 ; 0,999p / (0,994p +0,005) > 0,95.
0,999p >0,95 (0,994p +0,005).
0,999p > 0,9443 p + 0,00475.
0,0547 p >0,00475 ; p >0,087.
Partie C : Étude sur un échantillon
Pendant l’épidémie, on admet que la probabilité d’être atteint du chikungunya sur l’ile
de La Réunion est de 0,36.
On considère un échantillon de n individus choisis au hasard, en assimilant ce choix à un
tirage au sort avec remise. On désigne par X la variable aléatoire dénombrant le nombre
d’individus infectés dans cet échantillon parmi les n tirés au sort.
On admet que X suit une loi binomiale de paramètres n et p = 0,36.
Déterminer à partir de combien d’individus n la probabilité de l’évènement « au moins
un des n habitants de cet échantillon est atteint par le virus » est supérieure à 0,99. Expliquer la démarche.
On cherche la plus petite valeur de n tel que P(X > 1) >0,99.
1-P(X=0) >0,99 ; P(X=0) < 0,01.
P(X=0) =(1-0,36)n = 0,64n.
0,64n < 0,01 ; n ln(0,64 < ln(0,01) ; n > 10,31.
Il faut interroger au moins 11 individus.
|
|
|
|