Mathématiques, fonctions ; bac Asie 2025.

Mathématiques. Fonctions. Bac Asie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

... . .

.
..

.. ..
......

...

On considère les fonctions f et g définies sur l’intervalle ]0 ; +∞[ par :

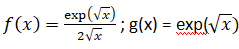1.a. Montrer que g ′ (x) = f (x) pour tout x de l’intervalle ]0 ; +∞[.

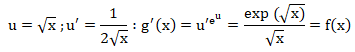b. Pour tout réel x de l’intervalle ]0 ; +∞[, calculer f ′ (x) et montrer que :

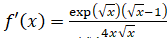
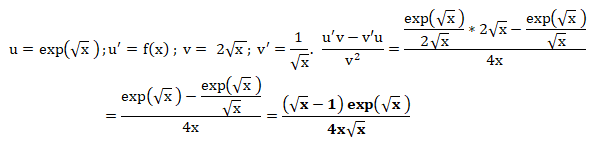2. a. Déterminer la limite de la fonction f en 0.
Le numérateur tend vers 1 ; le dénominateur tend vers 0 ; f(x) tend vers +oo.
b. Interpréter graphiquement ce résultat.
L'axe des ordonnées est asymptote à la courbe représentative de f(x).
3. a. Déterminer la limite de la fonction f en +∞.
Par croissance comparée, f(x) tend vers +oo.
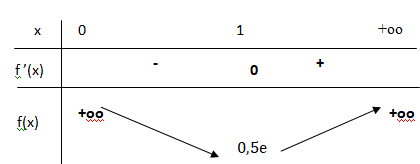
b. Étudier le sens de variation de la fonction f sur ]0 ; +∞[. Dresser le tableau de variations de la fonction f en y faisant figurer les limites aux bornes de l’intervalle de définition.

c. Montrer que l’équation f (x) = 2 admet une unique solution sur l’intervalle [1 ; +∞[ et donner une valeur approchée à 10⁻¹ près de cette solution.
f(x) est continue et strictement croissante sur [1 ; +oo[ et a valeurs dans [0,5 e ; +oo[. 2 appartient à cet intervalle.
D'après le corollaire du théorème de la valeur intermédiaire, f(x) = 2 admet une solution unique a dans cet intervalle
a ~4,6.
4. On pose.
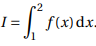
a. Calculer I.

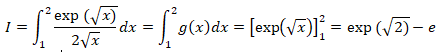b. Interpréter graphiquement le résultat.
I représente l'aire du domaine situé entre la courbe, l'axe des abscisses et les droites d'équation x=1 et x = 2.
5. On admet que la fonction f est deux fois dérivable sur l’intervalle ]0 ; +∞[ et que :

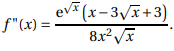a. En posant X = x^½, montrer que x −3 x^½ +3 > 0 pour tout réel x de l’intervalle ]0 ; +∞[.
f ''(X) =e^X(X²-3X+3) / (8X⁵).
f ''(X) a le signe de X²-3X+3.
.X²-3X+3=0.
Discriminant D =9-4*3=-3 < 0.
Donc .X²-3X+3 >0.
x −3 x^½ +3 > 0 pour tout réel x de l’intervalle ]0 ; +∞[.
b. Étudier la convexité de la fonction f sur l’intervalle ]0 ; +∞[.
f "(x) >0 sur ]0 ; +∞[. La fonction f est convexe sur cet intervalle.

... = =

....

Dans un laboratoire, on étudie une réaction chimique dans un réacteur fermé, sous certaines conditions. Le traitement numérique des données expérimentales a permis de modéliser l’évolution de la température de cette réaction chimique en fonction du temps. L’objectif de cet exercice est d’étudier cette modélisation.
La température est exprimée en degré Celsius et le temps est exprimé en minute. Dans tout l’exercice, on se place sur l’intervalle de temps [0 ; 10]. Les parties A et B peuvent être traitées de façon indépendante.
Partie A.
Dans un repère orthogonal du plan, on donne ci-dessous la courbe représentative de la fonction température en fonction du temps sur l’intervalle [0 ; 10].
1. Déterminer, par lecture graphique, au bout de combien de temps la température redescend à sa valeur initiale à l’instant t = 0.

On appelle f la fonction température représentée par la courbe ci-dessus. On précise que la fonction f est définie et dérivable sur l’intervalle [0 ; 10]. On admet que la fonction f peut s’écrire sous la forme f (t) = (at +b)e^−0,5t où a et b sont deux constantes réelles.
2. On admet que la valeur exacte de f (0) est 40. En déduire la valeur de b.
f(0) = 40 = b e⁰ = b
3. On admet que f vérifie l’équation différentielle (E) : y ′ +0,5y = 60e^−0,5t . Déterminer la valeur de a.
Calcul de f '(t) en posant u = at+40 et v = e^-0,5t ; u' = a ; v' = -0,5 e^-0,5t.
u'v+v'u = a e^-0,5t-0,5(at+40)e^-0,5t.=e^-0,5t(a -0,5at-20).
Repport dans (E) :
e^-0,5t(a -0,5at-20)+0,5 (at +40)e^−0,5t = 60e^−0,5t .
a -0,5at-20+0,5 (at +40)=60.
a-20+20=60 ; a = 60.

Partie B : Étude de la fonction f
On admet que la fonction f est définie pour tout réel t de l’intervalle [0 ; 10] par f (t) = (60t +40)e^−0,5t
1. Montrer que pour tout réel t de l’intervalle [0;10], on a : f ′ (t) = (40−30t)e^−0,5t .
On pose u = 60t+40 et v =e^−0,5t.
u' = 60 ; v' =-0,5e^−0,5t.
u'v+v'u = 60e^−0,5t-(30t+20)e^−0,5t = (40−30t)e^−0,5t .
2. a. Étudier le sens de variation de la fonction f sur l’intervalle [0;10]. Dresser le tableau de variations de la fonction f en y faisant figurer les images des valeurs présentes dans le tableau.
f '(t) a le signe de 40-30t.

b. Montrer que l’équation f (t) = 40 admet une unique solution α strictement positive sur l’intervalle ]0 ; 10].
c. Donner une valeur approchée de a au dixième près et en donner une interprétation dans le contexte de l’exercice.
Sur ]0 ; 4 /3], f(t) > 40 : l'équation f(t) = 40 n'a pas de solution.
Sur [4/3 ; 10] : f(4/3) >40 et f(10) < 40.
f(x) est continue et strictement décroissante sur [4/3 ; 10]. D'après le corollaire du théorème de la valeur intermédiaire, f(x) = 40 admet une solution unique a >0 dans cet intervalle.
a ~3,8.
3. On définit la température moyenne, exprimée en degré Celsius, de cette réaction chimique entre deux temps t₁ et t₂, exprimés en minute, par :

a. À l’aide d’une intégration par parties, montrer que
On pose u = 60t+40 et v' = e^-0,5t ; u'=60 ; v =-2 e^-0,5t .

b. En déduire une valeur approchée, au degré Celsius près, de la température moyenne de cette réaction chimique au cours des 4 premières minutes.
(320-800e^-2) / 4 ~53°C

menu