Mathématiques. Probabilités. Bac Centres étrangers 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
Un magasin est équipé de caisses automatiques en libre-service où le client scanne lui même ses articles. Le logiciel d’une caisse déclenche régulièrement des demandes de vérification. Un employé du magasin effectue alors un contrôle.
Partie A
Le contrôle peut être  :
- soit « total » : l’employé du magasin scanne alors à nouveau l’ensemble des articles du client;
-soit « partiel » : l’employé choisit alors un ou plusieurs articles du client pour vérifier qu’ils ont bien été scannés.
Si un contrôle est déclenché, il s’agit une fois sur dix d’un contrôle total. Lorsqu’un contrôle total est déclenché, une erreur du client est détectée dans 30 % des cas.
Lorsqu’un contrôle partiel est effectué, dans 85% des cas, il n’y a pas d’erreur.
Un contrôle est déclenché à une caisse automatique.
On considère les évènements suivants :
 T : « Le contrôle est un contrôle total »;
 E : « Une erreur est détectée lors du contrôle ».
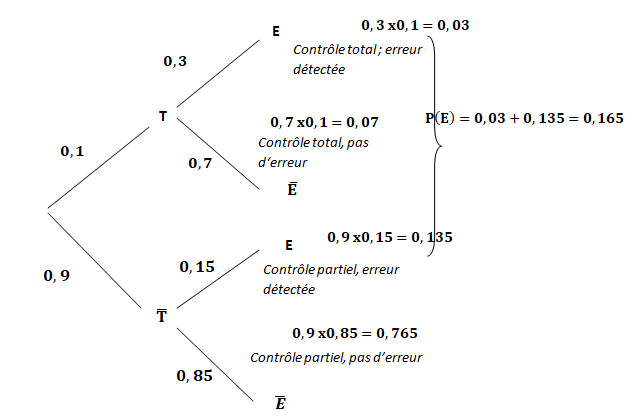
1. Construire un arbre pondéré représentant la situation puis déterminer P (non  T ∩E ) .
2. Calculer la probabilité qu’une erreur soit détectée lors d’un contrôle.

3. Déterminer la probabilité qu’un contrôle total ait été effectué, sachant qu’une erreur a été détectée. On donnera la valeur arrondie au centième.
PE(T)=+(T n E) / P(E)=0,1 x0,3 / 0,165 ~0,18.
Partie B
Sur une journée donnée, une caisse automatique déclenche 15 contrôles. La probabilité qu’un contrôle mette en évidence une erreur est p = 0,165. La détection d’une erreur lors d’un contrôle est indépendante des autres contrôles. On note X la variable aléatoire égale au nombre d’erreurs détectées lors des contrôles de cette journée.
 1. On admet que la variable aléatoire X suit une loi binomiale. Préciser ses paramètres.
n = 15 ; p = 0,165.
 2. Déterminer la probabilité qu’exactement 5 erreurs soient détectées. On donnera la valeur arrondie au centième.
P(X=5) =(155) x 0,1655 x0,83515-5~0,06.
3. Déterminer la probabilité qu’au moins une erreur soit détectée. On donnera la valeur arrondie au centième.
P(X >1) = 1-p(X=0)=1.0,83515 ~0,93.
4. On souhaite modifier le nombre de contrôles déclenchés par la caisse de manière à ce que la probabilité qu’au moins une erreur soit détectée chaque jour soit supérieure à 99%. Déterminer le nombre de contrôles, noté n,  que doit déclencher la caisse chaque jour pour que cette contrainte soit respectée.
Y variable aléatoire égale au nombre d'erreurs détectées  lors des contôles de la journée.
Y xuit la loi binomiale de paramètres n et p = 0,165.
P(Y >1) = 1-P(Y=0)=1-0,835n > 0,99.
0,01 >0,835n.
ln(0,01) > n ln(0,835), la fonction logarithme étant strictement croissante.
n > ln(0,01) / ln(0,835)  ; n > 25,5.
Il faut effectuuer 26 contrôles par jour.
Partie C
 Le magasin comporte trois caisses automatiques identiques qui, lors d’une journée, ont chacune déclenché 20 contrôles. On note X1, X2 et X3 les variables aléatoires associant à chacune des caisses le nombre d’erreurs détectées lors de cette journée. On admet que les variables aléatoires X1,X2 et X3 sont indépendantes entre elles et suivent chacune une loi binomiale B(20 ; 0,165).
 1. Déterminer les valeurs exactes de l’espérance et de la variance de la variable aléatoire X1.
E(X1) = n p = 20 x0,165=3,3.
V(X1) = n p (1-p)=20 x0,165 x0,835=2,756.
2. On définit la variable aléatoire S par S = X1 + X2 + X3. Justifier que E(S) = 9,9 et que V (S) = 8,2665.
E(S) = E(X1)+E(X2)+E(X3)=3 E(X1)=3 x3,3 = 9,9.
V(S) = V(X1)+V(X2)+V(X3)=3 V(X1) = 3 x2,756 =8,265.
  3. Pour cette question, on utilisera 10 comme valeur de E(S). À l’aide de l’inégalité de Bienaymé-Tchebychev, montrer que la probabilité que le nombre total d’erreurs sur la journée soit strictement compris entre 6 et 14 est supérieure à 0,48.
6 < S < 14 est équivalent à |S-10| < 4.
P( |S-10| < 4)=1-P( |S-10| > 4).
P( |S-10| > 4)< 8,265 / 42.
P( |S-10| < 4)=1-P( |S-10| > 4)>1-8,265 /16~0,48.

... =  =
....

 Le codage « base64 », utilisé en informatique, permet de représenter et de transmettre des messages et d’autres données telles que des images, en utilisant 64 caractères : les 26 lettres majuscules, les 26 lettres minuscules, les chiffres de 0 à 9 et deux autres caractères spéciaux.
Les parties A, B et C sont indépendantes.
Partie A
Dans cette partie, on s’intéresse aux séquences de 4 caractères en base64. Par exemple, « gP3g » est une telle séquence. Dans une séquence, l’ordre est à prendre en compte : les séquences « m5C2 » et « 5C2m » ne sont pas identiques.
1. Déterminer le nombre de séquences possibles.
Pour chaque caractère, il y a 64 possibilités.
Pour une séquence de 4 caractères, il y a 644 =16 777 216 possibilités
2. Déterminer le nombre de séquences si l’on impose que les 4 caractères sont différents deux à deux.
Arrangement de 4 caractères parmi 64 : 64 ! / (64-4)!=64 x63 x62 x61 =15 249 024.
 3. a. Déterminer le nombre de séquences ne comportant pas de lettre A majuscule.
Calcul identique à celui de la question 1 avec seulement 63 caractères.
634 = 15 752 961.
b. En déduire le nombre de séquences comportant au moins une lettre A majuscule.
644-634=1 024 255.
c. Déterminer le nombre de séquences comportant exactement une fois la lettre A majuscule.
A peut occuper l'une des 4 positions dans le code , les autres lettres étant différentes.
4 x633 = 1 000 188.
 d. Déterminer le nombre de séquences comportant exactement deux fois la lettre A majuscule.
(42) possibiltés pour la lettre A.
(42) x632 =23 814.
Partie B
On s’intéresse à la transmission d’une séquence de 250 caractères d’un ordinateur à un autre. On suppose que la probabilité qu’un caractère soit mal transmis est égale à 0,01 et que les transmissions des différents caractères sont indépendantes entre elles. On note X la variable aléatoire égale au nombre de caractères mal transmis.
1. On admet que la variable aléatoire X suit la loi binomiale. Donner ses paramètres.
n = 250 ; p = 0,01.
 2. Déterminer la probabilité que tous les caractères soient bien transmis. On donnera l’expression exacte, puis une valeur approchée à 10−3 près.
P(X=0)=(2500) x 0,010 x0,99250~0,081.
 3. Que pensez-vous de l’affirmation suivante : « La probabilité que plus de 16 caractères soient mal transmis est négligeable » ?
P(X >16)=P(X > 17)~1,04 10-9, valeur négligeable.
Partie C
On s’intéresse maintenant à la transmission de 4 séquences de 250 caractères. On note X1, X2, X3 et X4 les variables aléatoires correspondant aux nombres de caractères mal transmis lors de la transmission de chacune des 4 séquences. On admet que les variables aléatoires X1, X2, X3 et X4 sont indépendantes entre elles et suivent la même loi que la variable aléatoire X définie en partie B. On note S =  X1 + X2 + X3 + X4. Déterminer, en justifiant, l’espérance et la variance de la variable aléatoire S.
E(S) =E(X1)+E(X2)+E(X3)+E(X4)=4E(X)=4 n p=4 x250 x0,01= 10.
V(S) =V(X1)+V(X2)+V(X3)+V(X4)=4V(X)=4 n p(1-p)=4 x250 x0,01x0,99= 9,9.



  
menu