Mathématiques,Probabilités. Bac Centres étrangers 2025.

Mathématiques. Géométrie. Bac Centres étrangers 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

... . .

.
.

.. ..
......

...

Dans tout l’exercice, on considère que l’espace est muni d’un repère orthonormé. On considère :
les points A(−3 ; 1 ; 4) et B(1; 5; 2).
le plan P d’équation cartésienne 4x +4y −2z +3 = 0
la droite (d) dont une représentation paramétrique est :
x =-6+3t ; y = 1 ; z = 9-5t avec t réel.
1. Les droites (AB) et (d) sont :
a. sécantes non perpendiculaires.
b. perpendiculaires.
c. non coplanaires.
d. parallèles.
Vecteur directeur de la droite (AB) :
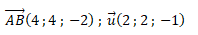
Vecteur directeur de la droite (d) :
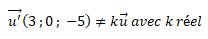
Les droites (AB) et (d) ne sont pas parallèles.

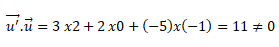Les droites (AB) et (d) ne sont pas perpendiculaires.

Equation paramétrique de la droite (AB) de vecteur directeur (2 ; 2 ; -1).
x = x_A+2s =-3+2s ; y = y_A +2s = 1+2s ; z=z_A-s =4-s avec t réel.
Les droites (AB) et (d) sont sécantes si :
-3+2s =-6+3t ; t = 1+2/3 s.
1+2s = 1 ; s = 0. Par suite t = 1.
4-s = 4 ; 9-5t = 9-5=4.
Le système admet une seule solution (s=0 ; t = 1). les droites (AB) et (d) sont sécantes.
.
2. La droite (AB) est :
a. incluse dans le plan P .
b. strictement parallèle au plan P .
c. sécante et non orthogonale au plan P .
d. orthogonale au plan P .
Coordonnées d'un vecteur normal au plan (P) : 4 ; 4 ; -2.
Coordonnées du vecteur AB : 4 ; 4 ; -2.
La droite (AB) est orthogonale au plan (P).

3. On considère le plan P’ d’équation cartésienne 2x + y +6z +5 = 0. Les plans P et P ′ sont :
a. sécants et non perpendiculaires.
b. perpendiculaires.
c. confondus.
d. strictement parallèles.
Coordonnées d'un vecteur normal au plan (P) :
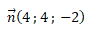Coordonnées d'un vecteur normal au plan (P') :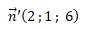
Ces deux vecteurs n'étant pas colinéaires, les plans (P) et (P') ne sont pas parallèles.

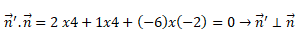
Les plans (P) et (p') sont perpendiculaires.

4. On considère le point C(0 ; 1 ; −1). La valeur de l’angle BAC arrondie au degré est :
a. 90°
b. 51°
c. 39°
d. 0.

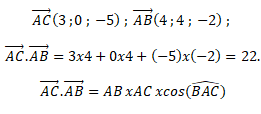
AC = (3²+0²+(-5)²)^½ =34^½.
AB = (4²+4²+(-2)²)^½ =36^½=6.
cos (BAC)=22 / (6 x34^½ )=0,329.
L'angle (BAC) mesure 51°.

... = =

....

On se place dans un repère orthonormé de l’espace. On considère les points :
A(1; 0; 3), B(−2 ; 1 ; 2) et C(0; 3; 2).
1. a. Montrer que les points A, B et C ne sont pas alignés.

Ces deux vecteurs n'étant pas colinéaires, les points A, B et C ne sont pas alignés.
b. Soit n le vecteur de coordonnées ( −1; 1; 4 ).
Vérifier que le vecteur n est orthogonal au plan (ABC).

Le vecteur n est orthogonal à deux vecteurs non colinéaires du plan(ABC), il est donc normal à ce plan.

c. En déduire que le plan (ABC) admet pour équation cartésienne −x + y +4z −11 = 0.
L'équation cartésienne de ce plan est : -x+y+4z+d=0.
A(1; 0; 3) appartient à ce plan : -1+0+4*3+d=0 ; d = -11.

On considère le plan P d’équation cartésienne 3x−3y+2z−9 = 0 et le plan P ′ d’équation cartésienne x − y − z +2 = 0.
2. a. Démontrer que les plans P et P ′ sont sécants.
Coordonnées d'un vecteur n normal au plan (P) : 3 ; -3 ; 2.
Coordonnées d'un vecteur n' normal au plan (P') : 1 ; -1 ; -1.
Ces deux vecteurs n'étant pas colinéaires, les plans P et P' ne sont ni parallèles ni confondus. Ils sont donc sécants.
On note (d) leur droite d’intersection
b. Déterminer si les plans P et P ′ sont perpendiculaires.

Les plans P et P ′ ne sont pas perpendiculaires.
3. Montrer que la droite (d) est dirigée par le vecteur u de coordonnées (1 ; 1 ; 0).
Il suffit de montrer que ce vecteur est contenu dans chaque plan P et P' :

La droite (d) est dirigée par le vecteur u(1 ; 1 ; 0).
4. Montrer que le point M(2; 1; 3) appartient aux plans P et P ′ . En déduire une représentation paramétrique de la droite (d).
3x_M−3y_M+2z_M−9 =3*2-3*1+2*3-9= 0 : M appartient au plan P.
x_M − y_M − z_M +2 = 2-1-3+2=0 : M appartient au plan P'.
Equation paramétrique de la droite (d) :
x = t+x_M=t+2 ; y = t+y_M = t+1 ; z = z_M=3.
5. Montrer que la droite (d) est aussi incluse dans le plan (ABC). Que peut-on dire des trois plans (ABC), P et P ′ ?
équation cartésienne du plan (ABC) : −x + y +4z −11 = 0.
Equation paramétrique de la droite (d) : x =t+2 ; y = t+1 ; z =3.
Intersection de la droite (d) et du plan (ABC) :
-t-2+t+1+4*3-11=0 est vérifié quelqie soit t.
La droite (d) appartient donc au plan (ABC).
La droite (d) appartient aux 3 plans (ABC), P et P'.
Coordonnées des vecteurs normaux aux trois plans :
(-1 ; 1 ; 4) ; (3 ; -3 ; 2) et (1 ; -1 ; -1).
Ces vecteurs n'étant pas colinéaires, les plans ne sont pas confondus, ils sont sécants.

menu