Mathématiques. Fonctions. Bac Centres étrangers 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . ... .. .. ...... ... Partie A On considère la fonction f définie sur l’intervalle ]−1 ; +∞[ par f (x) = 4ln(x +1)− x2/ 25 On admet que la fonction f est dérivable sur l’intervalle ]−1 ; +∞[. 1. Déterminer la limite de la fonction f en −1. ln(x+1) tend vers -oo ; -x2 / 25 tend vers -1/25. Par somme des limites, f(x) tend vers moins l'infini.  2. Montrer que, pour tout x appartenant à l’intervalle ]−1 ; +∞[ , on a : f ′ (x) = (100−2x −2x 2) /  (25(x +1)). f '(x) =4 /(x+1)-2x / 25=[4*25-2x(x+1)] / (25(x+1)]=(100-2x-2x2) / (25(x+1)).  3. Étudier les variations de la fonction f sur l’intervalle ]−1 ; +∞[ puis en déduire que la fonction f est strictement croissante sur l’intervalle [2; 6,5]. 25(x+1) est strictement positif ; f '(x) est du signe de 100-2x-2x2: Racines de 100-2x-2x2=0: discriminant (-2)2-4(-2)*100=804=22x201. x1 = (2+2*201½) / (-4)=-(1+201½) / 2 ~ -7,6 < -1 et x2 =-(1-201½) / 2~6,6. 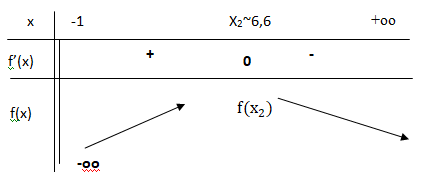La fonction f est strictement croissante sur l’intervalle [2; 6,5]. 4. On considère h la fonction définie sur l’intervalle [2; 6,5] par h(x) = f (x)− x. 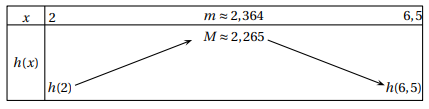On donne ci-dessous le tableau de variations de la fonction h : Montrer que l’équation h(x) = 0 admet une unique solution a appartenant à [2 ; 6,5]. h(2)=f(2)-2=4 ln(2+1)-22/25-2~2,23. Sur l'intervalle [2 ; m] la fonction h est strictement croissante et h(2) >0 : donc sur [2 ; m], h(x) >0 et h(x) = 0 n'admet pas de solution. Sur l'intervalle [m ; 6,5], la fonction h(x) est strictement décroissante et continue. h(m) = 2,265 >0 et h(6,5) = 4 ln(6,5+1)-6,52 /25-6,5 ~-0,13 < 0. 0 est compris entre h(m) et h(6,5). D'après le théorème des valeurs intermédiaires, l'équation h(x)=0 admet une solution unique a sur [m ; 6,5]. L’équation h(x) = 0 admet une unique solution a appartenant à [2 ; 6,5]. 6,36 < a <6,37.  5. On considère le script suivant, écrit en langage Python : a. Donner les valeurs renvoyées par la commande bornes(2). On donnera les valeurs arrondies au centième. 6,36 et  6,37.  b. Interpréter ces valeurs dans le contexte de l’exercice. 6,36 < a <6,37. Partie B Dans cette partie, on pourra utiliser les résultats obtenus dans la partie A. On considère la suite (un) définie par u0 = 2, et, pour tout entier naturel n, un+1 = f (un).  1. Montrer par récurrence que pour tout n entier naturel, 2 < un < un+1 < 6,5. Initialisation : u0 = 2 ; u1 = f(2)~4,23.La propriété est vraie au rang 0. Hérédité : 2 < un < un+1 < 6,5 est supposé vraie. f est strictement croissante sur [2 ; 6,5]. f(2) < f(un ) < f(un+1)< f( 6,5). Or f(2) >2 et f(6,5) ~6,37 <6,5. 2 < un+1 < un+2 < 6,5 . La propriété est vraie au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier naturel n. 2. En déduire que la suite (un) converge vers une limite L. La suite est croissante et majorée par 6,5, donc elle converge vers une limite L. 3. On rappelle que le réel a, défini dans la partie A, est la solution de l’équation h(x) = 0 sur l’intervalle [2; 6,5]. Justifier que L = a. L est solution de l'équation L = f(L). L appartient à [2 ; 6,5]. Sur cet intervalle l'équation h(x) =0 admet l'unique solution a. Donc a = L. ... =  = .... Partie A On considère la fonction f définie sur l’intervalle [0 ; +∞[ par : f (x) = 1 /(a +e −bx) où a et b sont deux constantes réelles strictement positives. On admet que la fonction f est dérivable sur l’intervalle [0 ; +∞[. La fonction f admet pour représentation graphique la courbe Cf ci-dessous :  On considère les points A(0; 0,5) et B(10; 1). On admet que la droite (AB) est tangente à la courbe Cf au point A. 1. Par lecture graphique, donner une valeur approchée de f (10). f(10) ~0,9. 2. On admet que la limite de f(x) en plus l'infini est f (x) = 1. Donner une interprétation graphique de ce résultat. Au voisinage de l'infini, Cf admet une droite asymptote d'équation y=1. 3. Justifier que a = 1. Au voisinage de l'infini, e-bx tend vers zéro et f(x) tend ver 1/a = 1 ; donc a = 1. 4. Déterminer le coefficient directeur de la droite (AB). (yB-yA) / (xB-xA)=(1-0,5) / (10-0) =0,05.  5. a. Déterminer l’expression de f ′ (x) en fonction de x et de la constante b. On pose u = 1 et v = a+e-bx ; u'=0 ; v' =-be-bx ; (u'v-v'u) / v2 =be-bx  / (a+e-bx)2.  b. En déduire la valeur de b. f '(0) = 0,05 =b / (a+1)2 =b /(1+1)2 ; b = 0,05 x 4 =0,2. Partie B On admet, dans la suite de l’exercice, que la fonction f est définie sur l’intervalle [0 ; +∞[ par : f (t) = e0,2x /(1+e0,2x). 1. Déterminer la limite en +oo de f (x). f(t) = 1/(1/e0,2x+1). 1/e0,2x tend vers zéro si x tend vers +oo. le dénominateur tend vbers1 et f(x) tend vers 1. 2. Étudier les variations de la fonction f sur l’intervalle [0 ; +∞[. On pose u = e0,2x et v = 1+e0,2x ; u' = 0,2xe0,2x ; v' = 0,2xe0,2x. (u'v-v'u) / v2 =0,2xe0,2x ( 1+e0,2x -e0,2x) / (1+e0,2x)2=0,2xe0,2x / (1+e0,2x)2 >0. La fonction f(x) est strictement croissante. 3. Montrer qu’il existe un unique réel a positif tel que f (a) = 0,97. La fonction f est continue et strictement croissante sur [0 ; +oo( et à valeurs dans [0,5 ; 1[. 0,97 appartient à  [0,5 ; 1[. D'après le corollaire du théorème  des valeurs intermédiaires, l'équation f(x) = 0,97 admet une solution unique a sur [0 ; +oo[. 4. À l’aide de la calculatrice, donner un encadrement du réel a par deux nombres entiers consécutifs. Interpréter ce résultat dans le contexte de l’énoncé. a ~17,4  ; a appartient à ]17 ; 18 [. Partie C 1. Montrer que, pour tout x appartenant à l’intervalle [0 ; +∞[, f (x) = e 0,2x /(1+e 0,2x). f(x) =1 /(1 +e −0,2x) . Multiplier numérateur et dénominateur par e0,2x : f (x) = e 0,2x /(1+e 0,2x).  2. En déduire une primitive de la fonction f sur l’intervalle [0 ; +∞[. On pose u(t) = 1+e0,2t ; u' = 0,2 e0,2t ; f (u)= 1 /0,2 u' / u = 5 u' / u. primitive de f : F = 5 ln((u) = 5 ln(1+e0,2t).   3. Calculer la valeur moyenne de la fonction f sur l’intervalle [0; 40]. On donnera la valeur exacte et une valeur approchée au millième.

menu