Mathématiques  ( spécialité), épreuve anticipée première générale . . . Sujet 1. QCM. 6 points 1. L’inverse du double de 5 est égal à  : le double de 5 est égal à 10 ; son inverse est 1/10. Réponse B. 2. On considère la relation F = a+b / (cd). Lorsque a = 0,5, b=3, c=4 et d = -0,25, la valeur de F est : F = 0,5 +3 /(-4 *0,25) = 0,5-3 = -2,5= -5 /2. Réponse A. . 3. Le prix d’un article est multiplié par 0,975. Cela signifie que le prix de cet article a connu : Prix initial : 100 ; prix final : 97,5 ; baisse 2,5 ( 2,5 %). Réponse A. 4. Le prix d’un article est noté P. Ce prix augmente de 10% puis baisse de 10%. A l’issue de ces deux variations, le nouveau prix est noté P1. On peut affirmer que : Après la première augmentation, le prix devient P+0,1 P = 1,1P. Baisse de 10 % : le prix est P1=1,1 x 0,9 P =0,99 P < P. Réponse C. 5. On lance un dé à 4 faces. La probabilité d’obtenir chacune des faces est donnée dans le tableau ci-dessous : Face numéro 1 Face numéro 2 Face numéro 3 Face numéro 4 0,5 1 / 6 0,2 x La valeur de x est : x = 1-0,5-1 / 6-0,2 = 0,3-1 /6 = 3/10 -1 /6 = 9 /30 -5 / 30 = 4 / 30 = 2 / 15. Réponse A. 6. On considère x, y, u des réels tels que 1 /x +1 /y = 1 /u. On peut affirmer que : réduire au même dénominateur : 1 / x +1 / y = (x+y) / (xy). prendre l'inverse : x y / (x+y) = u. Réponse A. 7. On a représenté ci-dessous la parabole d’équation y= x2. Soit l’inéquation (J), sur R, x2 ≥ 10. 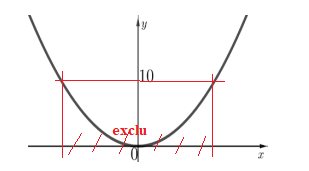L’inéquation (J) est équivalente à : x < -10½ ou x >10½. Réponse B. 8. On a représenté ci-dessous une droite D dans un repère orthonormé. 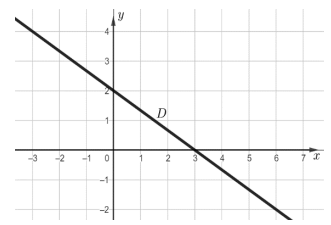Une équation de la droite D est : y = ax+b. Le point de coordonnées (0 ; 2) appartient à la droite : b =2. Le point de coordonnées (3 ; 0) appartient à la droite : 0 = 3a+2 ; a  -2 /3. y = -2x / 3+2  ou y /2 = -x /3+1 ou x/3 +y /2 -1=0. Réponse D. 9. On considère trois fonctions définies sur R : f1 ∶ y= x2 − (1 − x)2  ; f2 ∶ y= 0,5x-(1+1/2½) ; f3 ∶ y ⟼ (5-2x/3) / 0,7. Parmi ces trois fonctions, celles qui sont des fonctions affines sont : f1 : y = x2-(1+x2-2x) =2x-1. f1 et f2 et f3. Réponse B. 10. On a représenté ci-dessous une parabole P. Une seule des quatre fonctions ci-dessous est susceptible d’être représentée par la parabole P. Laquelle ? 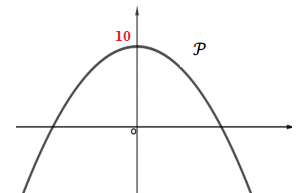y = -x2+10. Réponse C. 11. On a représenté ci-dessous la courbe C d’une fonction f. Les points A, B, R et S appartiennent à la courbe C. Leurs abscisses sont notées respectivement xA, xB, xR et xS. 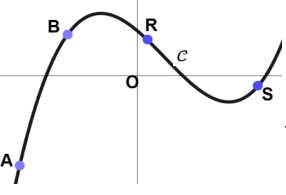L’inéquation x * f(x) > 0 est vérifiée par : x et f(x) doivent avoir le même signe. Points A et R. Réponse B. 11. Voici une série de notes avec les coefficients associés. Note 10 8 16 Coeficient 1 2 x On note m la moyenne. Que vaut x pour que m = 15 ? m = (10 +8*2+16x) / (3+x) = 15. 26+16x = 15(3+x)=45+15x ; x =45-26=19. Réponse D. Seconde partie. 14 points. 1. On considère la figure suivante, représentée dans un repère orthonormé. 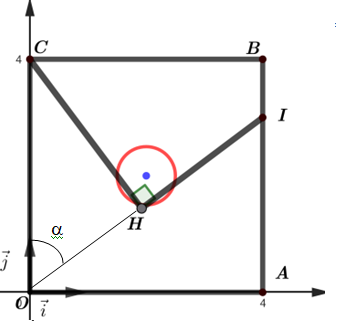On dispose des données suivantes :  - Le quadrilatère OABC est un carré de côté 4 ; - On a A(4 ; 0) ; B(4 ; 4) ; C(0 , 4) ; I(4 ; 3) - Le point H est le projeté orthogonal du point C sur la droite (OI) ; - On note e le cercle de centre D(2; 2) et de rayon 0,5. 1.a. Déterminer les coordonnées des vecteurs suivants :  b. En déduire le produit scalaire suivant. 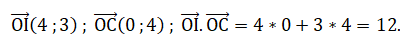 2. a. Exprimer le produit scalaire précédent en fonction des longueurs OH et OI. 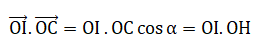b. Calculer la longueur OI. OI2 = OA2+AI2 =42+32=25 ; OI = 5. c. En déduire que OH = 2,4 . OI.OH = 12 ; 5 OI = 12 ; OI = 12 /5 = 2,4. 3. a. Déterminer une équation cartésienne de la droite (CH). 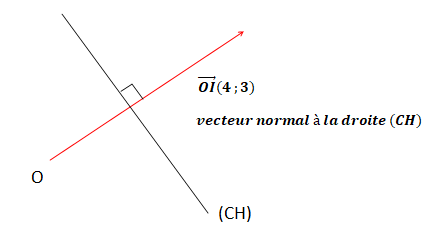Equation cartésienne de la droite (CH) : 4x+3y+c=0. C(0,4) appartient à cette droite : 0+3*4+c=0 ; c = -12. 4x+3y-12=0.  b. Justifier qu’une équation du cercle e est : x2 + y2 − 4x − 4y + 7,75 = 0 . Coordonnées du centre du cercle (2 ; 2) ; rayon R = 0,5. Equation du cercle : (x-2)2 +(y-2)2 = 0,52. x2-4x+4 +y2-4y+4 = 0,25 ; x2 + y2 − 4x − 4y + 7,75 = 0 .  c. Le point M(1,5; 2) appartient-il  à l’intersection du cercle e et de la droite (CH) ? Justifier. 1,52 + 22 − 4*1,5 − 4*2 + 7,75 =2,25+4-6-8+7,75= 0 est bien vérifiée ; M appartient donc au cercle. 4*1,5+3*2-12=0 est bien vérifié ; M appartient à la droite (CH). Exercice 2. On se place dans un repère  orthogonal. 1. On considère la fonction g définie pour tout réel x par g(x) = x2 − 5x + 4. On note P la courbe représentative de la fonction g. a. Étudier le signe de la fonction g sur R. Recherche des racines du trinôme x2-5x+4=0. Discriminant D =(-5)2 +4*4=9=32. Racines : x1 = (5+3) / 2 = 4 ; x2 = (5-3) / 2 = 1 ; Le coefficient de x2 étant positif : g(x) <0 sur ]1 ; 4[. g(x) = 0 si x=1 et si x =4. g(x) >0 sur ]-oo ; 1[ union ]4 ; +oo[.  b. On considère un entier naturel n quelconque. On note An le point de la courbe P d’abscisse n. On note an le coefficient directeur de la droite (AnAn+1). Justifier que pour tout entier naturel n, on a an = 2n − 4. An(n ; n2 − 5n + 4) ; An+1(n+1 ; (n+1)2 − 5(n+1) + 4) ; An+1(n+1 ; (n2+2n+1 − 5n-5 + 4) ; An+1(n+1 ; n2-3n) ; an=(n2-3n-(n2 − 5n + 4)) / (n+1-n)= 2n-4.  c. Quelle est la nature de la suite (an) ? an = 2n − 4 ; an+1 = 2(n+1) − 4 =2n-2=2n-4+6 = an+2. (an) est une suita arithmétique de raison 2 et de premier terme -4.  2. On considère la fonction f définie pour tout réel x de l’intervalle [0,5 ; 8] par f(x) = x − 5 + 4 / x .  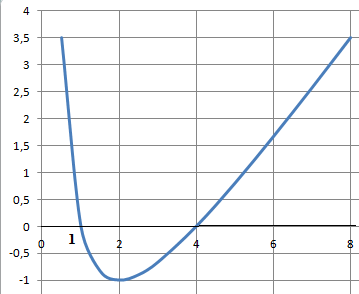On note C la courbe représentative de la fonction f. a. Vérifier que pour tout réel x, de l'intervalle [0,5; 8] on a f(x) = g(x) / x . g(x) =x2 − 5x + 4= x(x-5+4 /x) =x f(x) ; f(x) = g(x) / x. b. A l’aide de la question 1.a, déterminer la position de la courbe C par rapport à l’axe des abscisses. Sur [0,5 ; 1[, g(x) >0 et x >0 : f(x) >0 et C est au dessus de l'axe des abscisses. Sur ]1 ; 4[, g(x) <0 et x >0 : f(x) <0 et C est en dessous de l'axe des abscisses. Sur ][4 ; 8[, g(x) >0 et x >0 : f(x) >0 et C est au dessus de l'axe des abscisses. c. On admet que la fonction f est dérivable sur l’intervalle [0,5; 8]. Montrer que tout réel x de l’intervalle [0,5 ; 8] on a : f '(x)= (x-2)(x+2) / x2. f '(x) = 1-4 /x2=(x2-4) / x2 = (x+2)(x-2) / x2. d. En déduire le tableau de variations de la fonction f sur l’intervalle [0,5 ; 8]. 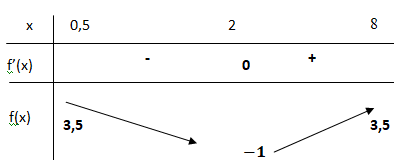e. Réaliser un schéma de l’allure de la courbe C sur lequel apparaîtront les résultats des questions 2.b et 2.d. Sujet 2 QCM ( 6 points) 1. On considère l’arbre de probabilité ci-dessous. On cherche la probabilité de l’évènement B. Réponse A. 2. Une tablette coûte 200 euros. Son prix diminue de 30%. Le prix après cette diminution est : 200 x(1-0,3)=200 x0,7 = 140 €. Réponse A. 3. Une réduction de 50% suivie d’une augmentation de 50% équivaut à : prix initial : 100 ; prix après réduction : 100 x0,5 = 50 ; prix après augmentation : 50 x1,5 = 75. Réduction de 25 %. Réponse B. 4. Dans un lycée, le quart des élèves sont internes, parmi eux, la moitié sont des filles. La proportion des filles internes par rapport à l’ensemble des élèves du lycée est égale à : Sur 200 élèves du lycée : 50 sont internes  ;  25 sont des internes filles soit 25 / 200 = 0,125 ( 12,5 %). Réponse B. 5. On considère le nombre N = 107 / 52= 100 x105 / 25 =4 105.Réponse D. 6. Un appareil a besoin d’une énergie de 7,5 × 106 Joules (J) pour se mettre en route. À combien de kiloWatts-heure (kWh) cela correspond-il ? 1 kWh = 3,6 106 J. (7,5 106) / (3,6 106)=7,5 / 3,6 ~2,08 kWh. Réponse B. 7. Le plan est muni d’un repère orthogonal. On note d la droite passant par les points A(0; −1) et B(2; 5). Le coefficient directeur de la droite d est égal à : (yB-yA) / (xB-xA) =6 /2 =3. Réponse C. 8. On a représenté ci-dessous une droite D. Parmi les quatre équations ci-dessous, la seule susceptible de représenter la droite D est : On recherche une fonction linéaire avec un coefficient négatif. 2x+y+1 et y = 2x-1 représentent des fonction affines. 2x-y=0  représente une fonction linéaire avec coefficient positif. y = x2-(x+1)2+1 =x2-(x2+2x+1)+1= -2x convient. Réponse C. 9. On note S l’ensemble des solutions de l’équation x2 = 10 sur R . On a : x =10½ et -10½. Réponse C. 10. La fonction f définie sur ℝ par f(x) = (3x − 15)(x + 2) admet pour tableau de signes : Réponse A. 11. L’expression développée de (2x + 0,5)2 est : 4x2 +2x+0,25. Réponse C. 12. Lorsqu’un point mobile suit une trajectoire circulaire de rayon R, en mètre (m), son accélération centripète a (en m/s²) s’exprime en fonction de la vitesse v (en m/s) de la manière suivante :a= v2 /R . L’expression permettant, à partir de cette formule, d’exprimer la vitesse v est : v = (a R)½. Réponse B. Exercice 1 . En 2020, une ville comptait 10 000 habitants. On modélise l’évolution du nombre d’habitants de cette ville par la suite (un) définie ainsi : un+1 = 1,08un − 300 , u0 = 10 000 ; où un représente le nombre d’habitants pour l’année 2020+n. 1. Indiquer ce que représente u1 et calculer sa valeur. u1 = 1,08 * 10 000-300=10 500 habitants en 2021. 2. On considère la suite (vn) définie pour tout entier naturel n par vn = un − 3750.  a. Déterminer v0. v0 = u0 − 3750= 10 000-3 750 = 6 250. b. Démontrer que pour tout entier naturel n, on a vn+1 = 1,08 vn. vn+1 = un+1 − 3750=1,08un − 300-3 750=1,08 un-4050=1,08(vn-3750)=1,08 vn.  c. En déduire la nature de la suite (vn). La suite (vn) est géométrique de raison 1,08 et de premier terme 6 250. d. Pour tout entier naturel n, exprimer, vn en fonction de n. vn = 6 250 x1,08n. e. En déduire que pour tout entier naturel n,on a un = 6250 × 1,08n + 3750. un = vn +3750=6250 × 1,08n + 3750.  3. Le tableau suivant, extrait d’une feuille automatisée de calcul, a été obtenue par recopie vers le bas après avoir saisie la formule suivante dans la cellule B2 : = 6250*1,08^A2 + 3750. n 9 10 11 12 un 14661 15318 18 322 19 488 La municipalité envisage d’ouvrir une nouvelle école maternelle dès que la population atteindra 19 000 habitants. La construction d’un tel établissement nécessitant deux ans, déterminer l’année à partir de laquelle la construction de l’école doit commencer. La nouvelle école sera nécessaire en 2020+12 = 2032. Les travaux doivent commencer en 2030. Exercice 2 Le plan est muni d’un repère orthogonal.  Partie A On considère la fonction P définie sur l’intervalle [−5 ; 3] par : P(x) = 2x2 + x − 10. 1. a. Déterminer les racines de P. 2x2+x-10=0. Discriminant D = 12+80=81=92. Racines x1 = (-1+9) / 4 = 2 ; x2 = (-1-9) / 4 = -2,5. b. En déduire l’axe de symétrie de la parabole d’équation y = P(x). (2-2,5) / 2= -0,25. Droite d'équation x = -0,25. 2. Etablir le tableau de signe de la fonction P sur l’intervalle [−5 ; 3]. Le coefficient de x2 étant positif : P(x) <0 sur ]-2,5 ; 2[. P(x) = 0 si x=-2,5 et si x =2. P(x) >0 sur ]-oo ; -2,5[ union ]2 ; +oo[. Partie B On considère la fonction f définie et dérivable sur l’intervalle [−5; 3] dont on donne  la courbe représentative Cf. La tangente T à la courbe Cf au point A d’abscisse 2 est horizontale.  1. Donner la valeur du nombre dérivé f '(2). 2. Résoudre, avec la précision permise par le graphique, l’inéquation f '(x) < 0. La courbe doit présenter un extrémum si f '(x) =0. x = -2,5 et x = 2.  3. On sait que la fonction f a pour expression sur l’intervalle [−5; 3] f(x)= (4x2 − 14x + 8)e0,5x. Démontrer que, pour tout x appartenant à l’intervalle [−5; 3], on a f '(x) = P(x)e0,5x . On pose u = 4x2-14x+8 et v = e0,5x ;  u' = 8 x-14 ; v' =0,5 e0,5x. u'v+v'u =(8 x-14 +0,5( 4x2-14x+8)e0,5x =(2x2+x-10)e0,5x =P(x)e0,5x 4. En utilisant les résultats de la partie A, dresser le tableau de variation de la fonction f sur l’intervalle [−5; 3]. e0,5x >0.  f '(x) a le signe de P(x).

menu