Mathématiques  ( non spécialité), épreuve anticipée première générale

.

. .
Sujet 1. QCM. 6 points
1. L’opération qui permet de calculer 25 % de 480 est :
480 x25 /100 = 480 / 4. Réponse D.

2. Le classement par ordre croissant des nombres suivants est :
1/5 =0,20 ; 19/100 =0,19 ; 0,21.
19 /100 ; 1/5 ; 0,21.  Réponse C.
.
3. Voici 4 nombres.

Le plus grand de ces 4 nombres est :
A =1 /(5 x5) =1 /25 ; B = 1 /(2x2x2x2x2) =1/ 32 ; C = 1 / 20 ; D = 1 /(3 x3 x3) = 1 /27.
Ces nombres ont le même numérateur ; le plus grand possède le plus petit dénominateur.
 Réponse C.

4. Un article augmente de 10% puis il augmente encore de 10%. Après ces deux augmentations il a augmenté de :
Prix initial : 100 ; après première augmentation 100 x1,1 = 110. Après seconde augmentation 110 x1,1 =121. (21 %)
  Réponse D.

5. . Le tiers d’un quart correspond à la fraction : 1 /3 x 1/4=1/12. Réponse D.

 6. On A =10+0,1+1 /1000 =10,1+0,001=10,101 .
Réponse C

7. A=1010+10-10~1010.
Réponse C

8. Une durée de 100 minutes correspond à : 1 h 40 min = 1 h + 40 / 60 h = 1 h+2 /3 h = 5 /3 h.
Réponse C.

9. . On considère une droite D représentée ci-dessous. La seule équation pouvant correspondre à l’équation réduite de la droite D est
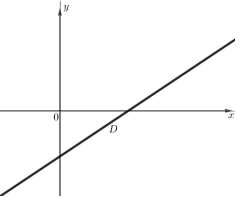
Le coefficient de x doit être positif et si x=0, y est négatif. Donc y = x-3.
Réponse B.

10. On considère la fonction f définie pour tout réel x par f(x) = 7 − 0,5 (x- 3)2. L’image de 3 par la fonction f est égale à :
f(3) =7. Réponse C.

11. Quand on développe (x − 3)2 on obtient : x2-6x+9
 Réponse D.

12. Voici 2 séries de valeurs : série A : 1 ; 2 ; 3 ; série B : 0,5 ; 2 ; 100
Série A : moyenne (1+2+3) / 3 = 2 ; médiane : 2.
Série B : moyenne (0,5+2+100) / 3 = 102,5 /3 ; médiane : 2.
Réponse C.

Seconde partie. 14 points.
1. Albert a acquis un étang d’une surface de 2 000 m2. Le jour de son anniversaire, un dimanche, il installe des nénuphars sur une surface de 200 m2. 1. Le dimanche d’après, la surface des nénuphars a augmenté de 40 m2.
a. Quel pourcentage d’augmentation cela représente-t-il ?
Nouvelle surface des nénuphars : 240 =200 x1,2 .
20 % d'augmentation.
b. Quelle est à présent la surface occupée par les nénuphars ?
2000+240=2240 m2.
2. Dans cette question, on suppose que la surface occupée par les nénuphars augmente de 40 m2 chaque semaine, depuis la date de l’anniversaire, tant que cela est possible.
a. Quelle sera la surface occupée par les nénuphars 10 semaines après l’anniversaire ?
200 +10 x40 =600 m2 .
b. Est-il possible qu’un dimanche, la surface occupée par les nénuphars soit égale à 580 m2 ? Justifier.
Non, 580 n'est pas un multiple de 40.
c. Au bout de combien de semaines, l’étang sera-t-il entièrement recouvert de nénuphars ?
2000-200=1800 ; 1800 / 40=45.
3. Dans cette question, on suppose que la surface occupée par les nénuphars augmente de 20 % chaque semaine, depuis la date de l’anniversaire, tant que cela est possible.
a. Quelle sera la surface occupée par les nénuphars 2 semaines après l’anniversaire ?
200 x1,2=240 ; 240 x1,2 =288 m2.
 b. On considère un entier naturel n. Déterminer, en fonction de n, la surface occupée par les nénuphars n semaines après l’anniversaire ?
Suite géométrique de raison 1,2 et de premier terme 200.
S = 200 x1,2n.
c. Au bout de combien de semaines, l’étang sera-t-il entièrement recouvert par les nénuphars ? On pourra s’aider du tableau ci-dessous..

200 x1,2n=2000 ; 1,2n = 10. n =13.
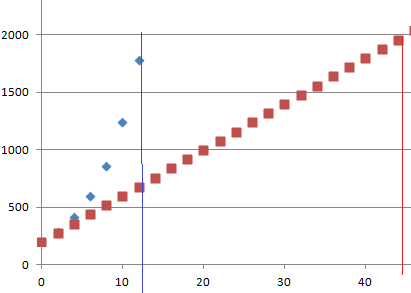
4. Réaliser sur votre copie un schéma sur lequel apparaissent l’allure des nuages de points traduisant la progression de la surface occupée par les nénuphars, aussi bien dans le cas de la question 2 que dans le cas de la question 3, et faire figurer le moment où, dans chacun des cas, l’étang est recouvert par les nénuphars.

Exercice 2.
Un vendeur de voitures possède un stock de 1000 voitures dont les caractéristiques sont résumées dans le tableau ci-dessous.

1. Indiquer ce que représente x et déterminer sa valeur.
x : nombre de voitures noires françaises.
x = 750-150-400=200
2. Quel est le pourcentage de voitures noires parmi les voitures du stock ?
250 / 1000 =0,25 (25 %).
 3. Quel est le pourcentage de voitures noires étrangères parmi les voitures du stock ?
50 / 1000 = 5 /100 (5 %).
 4. Quel est le pourcentage de voitures blanches parmi les voitures françaises ?
150 /750 =15 /75= 0,2 (20 %)
 5. Quel est le pourcentage de voitures françaises parmi les voitures blanches ?
150 / 250 =15 /25 =3 /5=0,6 (60%).
6. Alice et Benoît jouent au jeu suivant.
- Alice choisit au hasard une voiture parmi les voitures Françaises. Elle remporte 1 euro si ce n’est pas une voiture rouge.
- Benoit choisit au hasard une voiture parmi les voitures Blanches. Il remporte 1 euro si c’est une voiture étrangère. Lequel des deux a le plus dde chance de remporter 1 euro ?
Alice : probabilité de gain (150 +200) / 750=35 /75 = 7 / 15~0,46.
Benoit : probabilité de gain :100 /250 =0,25.


Exercice 3 .
 Sur un axe gradué en mètres, on organise une course entre une tortue et un escargot.
- La tortue part du point d’abscisse x = 0. Elle se déplace vers la droite à une vitesse de 2 mètres par minute.
- L’escargot part du point d’abscisse x = 12. Il se déplace vers la droite à une vitesse de 50 centimètres par minute.
- Les deux concurrents partent en même temps. A quel endroit la tortue rattrapera-t-elle l’escargot ?
La tortue  est à l'abscisse  x =2 t avec t en minute.
L'escargot est à l'abscisse x =12 +0,5 t.
2t = 12+0,5t ; 1,5t = 12 ; t = 12 /1,5 = 120 / 15 =8 minutes.
x= 2 x 8 =16 m.

Sujet 2
QCM ( 6 points)
1. On considère A = 1 /2 -1 / 2 x4 /3 =1 / 2-4 / 6=(3-4) / 6) = -1 /6.
Réponse B.
2. 4 croissants coûtent 6 euros. Combien coûtent 10 croissants :
6 / 4 x10 = 60 / 4 = 15 €.
 Réponse D.

3. Un prix a doublé. Cela signifie que le prix a augmenté de :
prix initial : 100 ; prix après augmentation: 200.
Augmentation de 100 %. Réponse B.

4. A l’issue d’une augmentation de 10%, un article coûte 110 euros.
Prix initial : x ; prix après augmentation : 1,1 x = 110 ; x = 100. ; augmentation 10 €.
Réponse C.

5. La masse d'un litre d'huile est égale à 900 g. La masse de 750 millilitres de cette huile est égale à :
900 x750 / 1000 = 9 x75 =675 g=0,675 kg. Réponse C.

6. Dans un repère du plan, on considère les points A(1 ; 100) et B (4 ; 106).
Le coefficient directeur de la droite (AB) est :
(yB-yA) / (xB-xA)=6 / 3 =2. Réponse A.

7. . Dans un repère du plan, on considère la droite D de coefficient directeur −0,1, passant par le point A(0 ; 4). On note B le point de la droite D dont l'abcisse est égale à 1. l'ordonnée du point B est :
(yB-yA) / (xB-xA)= -0,1 ; (yB-4) / (1-0)=yB-4 = -0,1 ; yB =3,9.
 Réponse B.

8. La forme développée de (x − 3)(x + 2) est :
x2-3x+2x-6=x2-x-6.
Réponse C.

9. Le volume V d’un cône de hauteur h et de rayon r est V = 1/ 3 p r2 h. On cherche à isoler h.
h =  3 V /(pr2). Réponse D.

10. On considère la fonction f définie sur R par f(x)= −2x2 + 3x + 1. L’image de −1 par la fonction f est égale à : f(-1) = -2 *1+3*(-1)+1= -4.
Réponse D.

11. On considère la fonction f définie sur R par f(x)= 2x2 − 5x + 3. Un antécédent de 0 par la fonction f est :
2x2-5x+3 = 0.
Discriminant D = (-5)2 -4*2*3=1 ;
racines : (5+1) / 4 =1,5 et (5-1) / 4 = 1.. Réponse A.

12. 12. On considère les deux séries ci-dessous.
Série A : 9 ; 10 ; 10 ; 11. Série B : 7 ; 10 ; 10 ; 13.
Série A : moyenne (9+10+10+11) / 4 =10
écart type : [(10-9)2 +(10-10)2 +(10-10)2 +(11-10)2 ] / 4=2 /4 =0,5
Série B : moyenne(7+10+10+13) / 4 = 10.
écart type : [(10-7)2 +(10-10)2 +(10-10)2 +(13-10)2 ] / 4=18 / 4 =4,5. Réponse D.

Exercice 1 . 

On étudie la croissance d’une population de champignons.
Partie A.
Au début de l’expérience, on dispose de  champignons. Toutes les dix minutes, on mesure l’évolution de leur nombre. On obtient les résultats suivants



Soit n un entier naturel. On note un le nombre de champignons après n périodes de dix minutes. Ainsi u0 = 100, u1 = 125, u2 = 150…
 1. Justifier que les termes u0, u1, u2, u3 sont en progression arithmétique.
u1 = u0+25 ; u2 = u1+25 ; u3 = u2+25 ;
2. En supposant que la population de champignons continue d’évoluer selon le même rythme, montrer qu’elle aura quadruplé deux heures après le début de l’expérience.
2 heures = 12 x 10 minutes.
u12 = u0+12 x25=100 +300=400.
 Partie B.
En réalité, on constate que la population de champignons a quadruplé 80 minutes après le début de l’expérience. De nouvelles mesures donnent les résultats suivants. Soit n un entier naturel. On note vn le nombre de champignons, après n périodes de quarante minutes. Ainsi v0 = 100, v1 = 200, v2 = 400 …
 1. Montrer que les termes v0, v1, v2, v3 sont en progression géométrique.
v1 = 2x v0 ; v2 = 4x v0 = 22 v0 ; v3 = 8x v0 = 23 v0 ;
2. On suppose que la suite (vn) est une suite géométrique de raison 2. Indiquer sans justifier lequel des 4 graphiques ci-dessous est susceptible de représenter cette suite.

3. Quel sera le nombre de champignons quatre heures après le début de l’expérience ?
4 h =240 min= 6 x 40 minutes.
v6= 26 v0 = 64 x100=6400.
4. Cinq heures après le début de l’expérience, on dénombre environ 18 000 champignons. Est-ce cohérent avec le modèle choisi ?
v7= 27 v0 = 128 x100=12800.
v8= 287 v0 = 256 x100=25600.
5 h = 300 min = 7,5 x 40 min.
18 000 est compris entre 12800 et 25 600; c'est donc cohérent.

Exercice 2.
Partie A.
Dans un lycée comptant 2000 élèves, on donne la répartition des effectifs suivant le sexe et le choix de la LV1.

Filles
 Garçons
Anglais
 712
 728
Autres LV1
 288
 272

 1. Un élève affirme « Dans ce lycée, il y a autant de filles que de garçons ». A-t-il raison ? Justifier.
Nombre de filles : 712+288 =1000 ; nombre de garçons : 728+272 = 1000. Il a donc raison.
On choisit au hasard, de manière équiprobable, un élève dans ce lycée. On considère les événements suivants :
F :« l’élève est une fille » ; A : « l’élève a choisi Anglais pour LV1 ». Dans les questions qui suivent, on donnera les résultats sous forme d’une fraction qu’il n’est pas demandé de simplifier.
2. Déterminer la probabilité de l’événement A ∩ F.
712 / 2000 =0,356.
3. Déterminer la probabilité de l’événement A sachant que l’événement F est réalisé.
PF(A) =P(A ∩ F) / P(F) = 0,356 / 0,5 =0,712.
4. Les événements A et F sont-ils indépendants ? Justifier.
P(A)=(712+728) / 2000 =0,72.
P(F) = 0,5.
P(A) x P(F) = 0,36 diffère de P(A ∩ F).
Les évenements A et F ne sont pas indépendants.
 5. On sait que l’élève choisi est un garçon. On considère l’affirmation suivante :
« La probabilité qu’il ait choisi Anglais pour LV1 est plus de trois fois plus grande que la probabilité qu’il n’ait pas choisi Anglais pour LV1 ». Cette affirmation est-elle vraie ? Justifier.
P(A) = 728 / 1000 = 0,728.
P(non A) =272 /1000=0,272.
0,272 x3 = 0,816 > 0,728.
L'affirmation est fausse.

 Partie B. On dispose d’une pièce de monnaie truquée pour laquelle la probabilité d’obtenir pile lors d’un lancer est égale à 0,25 .
 1. Déterminer la probabilité d’obtenir face.
1-0,25=0,75.
2. On lance trois fois de suite cette pièce de monnaie, les trois lancers étant indépendants, et on note pour chaque lancer le résultat (pile ou face) obtenu.
a. Représenter la situation par un arbre de probabilités.

b. Quelle est la probabilité d’obtenir exactement une fois pile lors de ces trois lancers ?
0,75 x0,75 x0,25 + 0,25 x0,75 x0,75 +0,25 x0,75 x0,75 =3( 3 /4 x3 /4 x1 /4 )= 27 / 64.
c. Quelle est la probabilité de ne jamais obtenir pile ?
0,75 x0,75 x0,75 = 3 /4 x3 /4 x3/4 =27 /64.

Sujet 3.
QCM(6 points)
1. Donner un ordre de grandeur de 101 × 99 :
100 x 100 = 10 000 . Réponse C.

2. Un prix augmente de 20% puis diminue de 20%.
Prix initial 100 ; prix après augmentation : 120 ; prix après diminution : 120 x0,8 =96 < 100. Réponse C.

3. Par combien faut-il multiplier une quantité positive pour que celle-ci diminue de 2,3 %.
1-0,023 = 0,977. Réponse B.

4. Dans un lycée, 50 élèves étudient le Grec, ce qui représente 4% de du nombre d’élèves inscrits dans ce lycée. Le nombre d’élèves inscrits dans ce lycée est égal à :
50 / 0 04=5000 / 4=1250.  Réponse D.

5. Le volume d’un glacier diminue de 3 % chaque année. Si V(n)) désigne le volume du glacier pour l’année n on a :
V(n+1) = 0,97 V(n). Réponse C.

6. Dans un repère du plan on a représenté une droite. Le coefficient directeur de cette droite est égal à :

Ce coefficient est négatif et vaut : -3 /1 =-3. Réponse A.

7. Dix stylos coûtent en tout 13 euros. Le prix de trois stylos est égal à :
13 / 10 x3 =1,3 x3 =3,9 €.. Réponse C.

8. Une athlète parcourt 1 km en 5 minutes. Quelle est sa vitesse moyenne ?
5 min = 1 /12 h ; 1 / (1/12) = 12 km /h. Réponse C.

9. Sur 60 personnes présentes à une exposition, on distingue trois groupes :
 groupe A : 30 personnes (50 %)
 groupe B : 12 personnes (12 /60 =0,2 (20 %).
 groupe C : les autres. (30 %). Quelle représentation décrit la situation ?

10. On considère les deux séries ci-dessous.
Série A : 9 ; 10 ; 10 ; 11
Série B : 7 ; 10 ; 10 ; 13.
Série A : moyenne (9+10+10+11) / 4 =10
écart type : [(10-9)2 +(10-10)2 +(10-10)2 +(11-10)2 ] / 4=2 /4 =0,5
Série B : moyenne(7+10+10+13) / 4 = 10.
écart type : [(10-7)2 +(10-10)2 +(10-10)2 +(13-10)2 ] / 4=18 / 4 =4,5. Réponse D.

11. Le volume V d’un cylindre de hauteur h et de rayon r est V = p r2 h. On cherche à isoler h.
h =  V /(pr2). Réponse C.
12. Soit f une fonction définie sur l’intervalle [−4 ; 4] dont la représentation graphique est donnée. L’ensemble  des solutions de l’équation f(x)= 0 est :

-3 ; -1 ; 1 ; 2. Réponse C.


  
menu