Mathématiques. Probabilités. Bac Métropole 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
On compte quatre groupes sanguins dans l’espèce humaine : A, B, AB et O. Chaque groupe sanguin peut présenter un facteur rhésus. Lorsqu’il est présent, on dit que le rhésus est positif, sinon on dit qu’il est négatif. Au sein de la population française, on sait que :
45 % des individus appartiennent au groupe A, et parmi eux 85 % sont de rhésus positif;
 10 % des individus appartiennent au groupe B, et parmi eux 84 % sont de rhésus positif;
 3 % des individus appartiennent au groupe AB, et parmi eux 82 % sont de rhésus positif.
On choisit au hasard une personne dans la population française. On désigne par :
 A l’évènement « La personne choisie est de groupe sanguin A »;
 B l’évènement « La personne choisie est de groupe sanguin B »;
 AB l’évènement « La personne choisie est de groupe sanguin AB »;
 O l’évènement « La personne choisie est de groupe sanguin O »;
 R l’évènement « La personne choisie a un facteur rhésus positif ».

 1. Recopier l’arbre ci-dessous en complétant les dix pointillés.

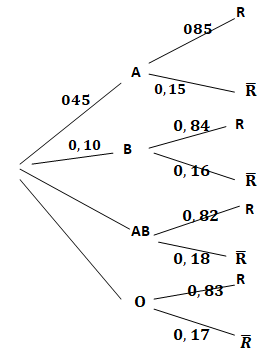2. Montrer que P(B ∩R) = 0,084. Interpréter ce résultat dans le contexte de l’exercice.
P(B ∩R)=P(B) x PB(R)=0,10 x0,84 = 0,084.
8,4 % de la population est de groupe sanguin B et de rhésus positif.
  3. On précise que P(R) = 0,8397. Montrer que PO (R) = 0,83.
D'après la formule des probabilités totales :
P(R) = P(A n R) + PB n R) + P(AB n R) + P(O n R) ;
P(O n R) =P(R) -P(A n R) - PB n R) - P(AB n R) =0,8397-0,45 x0,85 -0,084-0,03x0,82 =0,3486.
 PO (R)=P(O n R) / P(O) =0,3486 / 0,42 = 0,83.
 4. On dit qu’un individu est « donneur universel » lorsque son sang peut être transfusé à toute personne sans risque d’incompatibilité. Le groupe O de rhésus négatif est le seul vérifiant cette caractéristique. Montrer que la probabilité qu’un individu choisi au hasard dans la population française soit donneur universel est de 0,071 4.
P(O n non R) =P(O) x PO(non R)=P(O) x (1-PO(R))=0,42 x(1-0,83) = 0,0714.

5. Lors d’une collecte de sang, on choisit un échantillon de 100 personnes dans la population d’une ville française. Cette population est suffisamment grande pour assimiler ce choix à un tirage avec remise. On note X la variable aléatoire qui à chaque échantillon de 100 personnes associe le nombre de donneurs universels dans cet échantillon.
 a. Justifier que X suit une loi binomiale dont on précisera les paramètres.
On répète 100 fois de manière identique et indépendante une expérience aléatoire présentant deux issues :
succès : " donneur universel" p = 0,0714.
X compte le nombre de succès.
X suit la loi binomiale  de paramètres : n = 100 ; p = 0,0714.
b. Déterminer à 10−3 près la probabilité qu’il y ait au plus 7 donneurs universels dans cet échantillon.
P(X < 7) = 0,577.
c. Montrer que l’espérance E(X) de la variable aléatoire X est égale à 7,14 et que sa variance V (X) est égale à 6,63 à 10−2 près.
E(X) = n p = 100 x0,0714 = 7,14.
V(X) = n p (1-p) = 100 x0,0714 x(1-0,0714) ~6,63.
6. Lors de la semaine nationale du don du sang, une collecte de sang est organisée dans N villes françaises choisies au hasard numérotées 1,2, 3, ... , N où N est un entier naturel non nul. On considère la variable aléatoire X1 qui à chaque échantillon de 100 personnes de la ville 1 associe le nombre de donneurs universels dans cet échantillon. On définit de la même manière les variables aléatoires X2 pour la ville 2, ... , XN pour la ville N. On suppose que ces variables aléatoires sont indépendantes et qu’elles admettent la même espérance égale à 7,14 et la même variance égale à 6,63. On considère la variable aléatoire MN = (X1 + X2 +...+ XN)/ N .
a. Que représente la variable aléatoire MN dans le contexte de l’exercice ?
Nombre moyen de donneurs universels parmi ces N collectes de sang.
 b. Calculer l’espérance E(MN ).
E(MN )= E(X) = 7,14.
c. On désigne par V (MN ) la variance de la variable aléatoire MN . Montrer que V (MN ) = 6,63 /N .
V(MN) = V(X) / N = 6,63 / N.
d. Déterminer la plus petite valeur de N pour laquelle l’inégalité de BienayméTchebychev permet d’affirmer que :
P(|Mn-7,14|<0,14) >0,95.
1-(6,63 / N) / 0,142 > 0,95 ;
 1-6,63 /(N x0,142) >0,95.
-6,63 /(N x0,142) > -0,05
6,63 /(N x0,142) < -0,05
0,0196 N / 6,63 > 1 /0,05
N > 6,63 / (0,05 x0,0196)~ 6766.

... =  =
....

 Dans cet exercice on s’intéresse à des personnes venues séjourner dans un centre multisports au cours du week-end. Les résultats des probabilités demandées seront arrondis au millième si nécessaire.
Partie A
Le centre propose aux personnes venues pour un week-end une formule d’initiation au roller composée de deux séances de cours. On choisit au hasard une personne parmi celles ayant souscrit à cette formule. On désigne par A et B les évènements suivants :
 A : « La personne chute pendant la première séance »;
 B : « La personne chute pendant la deuxième séance ».
 Des observations permettent d’admettre que P(A) = 0,6. De plus on constate que :
 Si la personne chute pendant la première séance, la probabilité qu’elle chute pendant la deuxième est de 0,3;
  Si la personne ne chute pas pendant la première séance, la probabilité qu’elle chute pendant la deuxième est de 0,4.
1. Représenter la situation par un arbre pondéré.

2. Calculer la probabilité P (non A ∩ non B ) et interpréter le résultat.
P(non A n non B) = P(non A) n Pnon A (non B) =0,4 x0,6 = 0,24.
La probabilité qu'une personne ne chute pas au cours des deux premières séances est 0,24.
3. Montrer que P(B) = 0,34.
Formule des probabilités totales :
P(B) = P(A) x PA(B) +Pnon A (B)=0,18 + 0,16 = 0,34.
4. La personne ne chute pas pendant la deuxième séance de cours. Calculer la probabilité qu’elle n’ait pas chuté lors de la première séance.
Pnon B(non A) = P(non A n non B) / P(non B) =0,24 / 0,66 ~0,364.
5. On appelle X la variable aléatoire qui, à chaque échantillon de 100 personnes ayant souscrit à la formule, associe le nombre d’entre elles n’ayant chuté ni lors de la première ni lors de la deuxième séance. On assimile le choix d’un échantillon de 100 personnes à un tirage avec remise. On admet que la probabilité qu’une personne ne chute ni lors de la première ni lors de la deuxième séance est de 0,24.
a. Montrer que la variable aléatoire X suit une loi binomiale dont on précisera les paramètres.
On répète 100 épreuves indépendantes de Bernoulli ( succès = pas de chute) de paramètres p = 0,24 ;
X suit la loi binomiale de paramètres n = 100 ; p = 0,24.
b. Quelle est la probabilité d’avoir, dans un échantillon de 100 personnes ayant souscrit à la formule, au moins 20 personnes qui ne chutent ni lors de la première ni lors de la deuxième séance ?
P(X > 20) ~0,855.
c. Calculer l’espérance E(X) et interpréter le résultat dans le contexte de l’exercice.
E(X) = n p = 100 x0,24 = 24.
En moyenne sur 100 personnes, 24 personnes ne chutent  pas au cours des deux premières séances.
 Partie B
On choisit au hasard une personne venue un week-end au centre multisport. On note T1 la variable aléatoire donnant son temps d’attente total en minute avant les accès aux activités sportives pendant la journée du samedi et T2 la variable aléatoire donnant son temps d’attente total en minutes avant les accès aux activités sportives pendant la journée du dimanche. On admet que :
 T1 suit une loi de probabilité d’espérance E(T1) = 40 et d’écart-type s(T1) = 10;
 T2 suit une loi de probabilité d’espérance E(T2) = 60 et d’écart-type s(T2) = 16;
 les variables aléatoires T1 et T2 sont indépendantes. On note T la variable aléatoire donnant le temps total d’attente avant les accès au activités sportives lors des deux jours, exprimé en minute. Ainsi on a T = T1 +T2.
 1. Déterminer l’espérance E(T ) de la variable aléatoire T . Interpréter le résultat dans le contexte de l’exercice.
E(T) = E(T1+T2)=E(T1)+E(T2)=40+60=100.
En moyenne une personne attend 100 minutes pour accéder aux activités sportives durant le week-end.
2. Montrer que la variance V (T ) de la variable aléatoire T est égale à 356.
Pour deux variables indépendantes : V(X+Y)=V(X)+V(Y)= s2(T1)+s2(T2)=102+162=356.
3. À l’aide de l’inégalité de Bienaymé-Tchebychev, montrer que, pour une personne choisie au hasard parmi celles venues un week-end au centre multisports, la probabilité que son temps total d’attente T soit strictement compris entre 60 et 140 minutes est supérieure à 0,77.
P(|T-E(T)|> k )< V(X) / k2 .
k = 40 par rapport à la moyenne 100.
P(|T-100|> 40 )< 356 / 402=0,2225.
P(60 < T <140) = P([T-100| <40) > 1-0,2225 = 0,7775.
Cette valeur est bien supérieure à 0,77.



  
menu