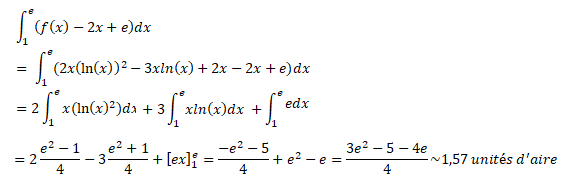Mathématiques. Fonctions. Bac Métropole 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . . . .. .. ...... ... On considère une fonction f définie sur l’intervalle ]0 ; +∞[. On admet qu’elle est deux fois dérivable sur l’intervalle ]0 ; +∞[. On note f ′ sa fonction dérivée et f ′′ sa fonction dérivée seconde. 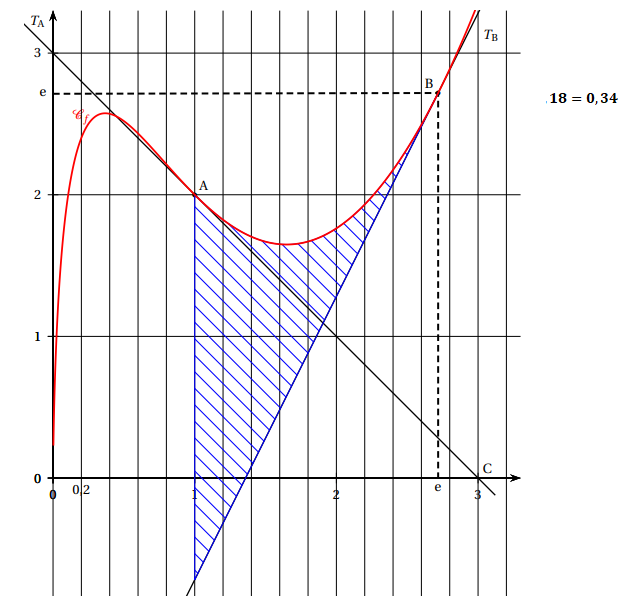Dans un repère orthogonal, on a tracé ci-dessous :  la courbe représentative de f , notée Cf sur l’intervalle ]0; 3];  la droite TA,tangente à Cf au point A(1; 2);  la droite TB tangente à Cf au point B(e; e).  On précise par ailleurs que la tangente TA passe par le point C(3; 0). On répondra aux questions suivantes en les justifiant à l’aide du graphique. 1. Déterminer le nombre dérivé f ′ (1). f '(1) = coefficient directeur de la droite TA =-3 / 3 = -1.  2. Combien de solutions l’équation f ′ (x) = 0 admet-elle dans l’intervalle ]0; 3] ? Cf présente un minimum et un  maximum : f '(x) =0 admet donc deux solutions dans l’intervalle ]0; 3] 3. Quel est le signe de f ′′(0,2) ? En x = 0,2, la fonction est concave : f "(0,2) est donc négative. Partie B : étude de la fonction f.  On admet dans cette partie que la fonction f est définie sur l’intervalle ]0 ; +∞[ par f (x) = x[2(lnx) 2 −3ln(x) +2] où ln désigne la fonction logarithme népérien. 1. Résoudre dans R l’équation 2X 2 −3X +2 = 0. En déduire que Cf ne coupe pas l’axe des abscisses. Discriminant : (-3)2 -2 x4 x2 = -7, donc pas de  racines réelles. Si Cf coupe l'axe des abscisses, alors f(x) =0. 2(lnx) 2 −3ln(x) +2 s'écrit en posant X = ln(x) : 2X 2 −3X +2. Or  .2X 2 −3X +2 = 0 ne possède pas de racines réelles. Donc f(x)=0 n'a pas de solutions réelles et Cf ne coupe pas l'axe des abscisses.  2. Déterminer, en justifiant, la limite de f en +∞. On admettra que la limite de f en 0 est égale à 0. x et ln(x) tendent vers +oo.Par somme et produit des limites, f(x) tend vers +oo. 3. On admet que pour tout x appartenant à ]0 ; +∞[, f ′ (x) = 2(lnx) 2 +lnx −1.  a. Montrer que pour tout x appartenant à ]0 ; +∞[, f ′′(x) =  (4lnx +1) / x. f "(x) = 4 lln(x) / x +1/x = (4 ln(x) +1) / x. b. Étudier la convexité de la fonction f sur l’intervalle ]0 ; +∞[ et préciser la valeur exacte de l’abscisse du point d’inflexion. x >0 ; f'(x) a le signe de 4 ln(x)+1. 4 ln(x) +1=0 ; ln(x) =- 0,25 ; x = e-0,25. f "(x) > 0 sur [e-0,5 ; +oo[ et la fonction est convexe sur cet intervalle. f"(x) <0 sur ]0 ; e-0,25] et la fonction est concave sur cet intervalle. Abscisse du point d'inflexion : e-0,5.  c. Montrer que la courbe Cf est au-dessus de la tangente TB sur l’intervalle ]1 ; +∞[.  La fonction est convexe sur ]1 ; +∞[ : la courbe Cf est au dessus de toutes ses tangentes. Partie C : Calcul d’aire 1. Justifier que la tangente TB a pour équation réduite y = 2x −e. y = f '(e) (x-e) +f(e). f '(e) = 2(ln(e))2+ln(e) -1=2+1-1=2. f(e) = e[(ln(e))2-3ln(e)+2]=e. Equation de TB : y = 2(x-e)+e = 2x-e. 2. 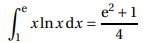À l’aide d’une intégration par parties, montrer que  On pose u = ln(x) et v' = x ; u' = 1 /x ; v = ½x2. 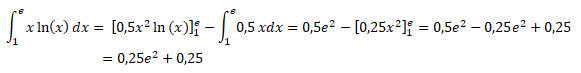  3. On note A l’aire du domaine hachuré sur la figure, délimité par la courbe Cf , la tangente TB, et les droites d’équation x = 1 et x = e. On admet que 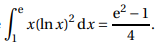 4 . En déduire la valeur exacte de A en unité d’aire. L'aire hachurée est délimitée par la courbe Cf, la tangente TB et les droites d'équation x = 1 et x = e. ... =  = .... L’objet de cet exercice est l’étude de l’arrêt d’un chariot sur un manège, à partir du moment où il entre dans la zone de freinage en fin de parcours. On note t le temps écoulé, exprimé en seconde, à partir du moment où le chariot arrive sur la zone de freinage. On modélise la distance parcourue par le chariot dans la zone de freinage, exprimée en mètre, en fonction de t, à l’aide d’une fonction notée d définie sur [0 ; +∞[. On a ainsi d(0) = 0. Par ailleurs, on admet que cette fonction d est dérivable sur son ensemble de définition. On note d ′ sa fonction dérivée. Partie A Sur la figure  ci-dessous, on a tracé dans un repère orthonormé :  la courbe représentative Cd de la fonction d ; la tangente T à la courbe Cd au point A d’abscisse 4,7;  l’asymptote D à Cd en +∞. Dans cette partie, aucune justification n’est attendue. Avec la précision que permet le graphique, répondre aux questions ci-dessous. D’après ce modèle : 1. Au bout de combien de temps le chariot aura-t-il parcouru 15 m dans la zone de freinage ? f(2) = 15 ; le chariot parcourt 15 m en 2 s. 2. Quelle longueur minimale doit-être prévue pour la zone de freinage ? 23 m. 3. Que vaut d ′ (4,7) ? Interpréter ce résultat dans le contexte de l’exercice. La tangente en A passe par les points de coordonnées (0 ; 16,5) et (4,7 ; 21). Coeficient directeur de la tangente  en A : (21-16,5) / (4,7-0) ~0,96. Partie B On rappelle que t désigne le temps écoulé, en seconde, à partir du moment où le chariot arrive sur la zone de freinage. On modélise la vitesse instantanée du chariot, en mètre par seconde  en fonction de t, par une fonction v définie sur [0 ; +∞[. On admet que :  la fonction v est dérivable sur son ensemble de définition, et on note v ′ sa fonction dérivée;  la fonction v est une solution de l’équation différentielle (E) : y ′ +0,6y = e −0,6t , où y est une fonction inconnue et où y ′ est la fonction dérivée de y. On précise de plus que, lors de son arrivée sur la zone de freinage, la vitesse du chariot est égale à 12 m.s−1 , c’est-à-dire v(0) = 12. 1. a. On considère l’équation différentielle (E ′ ) : y ′ +0,6y = 0. Déterminer les solutions de l’équation différentielle (E ′ ) sur [0 ; +∞[. f(t) = A exp(-0,6 t) avec A une constante réelle.  b. Soit g la fonction définie sur [0 ; +∞[ par g(t) = t e −0,6t . Vérifier que la fonction g est une solution de l’équation différentielle (E). On calcule g'(t) en posant u = t et v = exp(-0,6t) ; u' = 1 ; v' = -0,6 exp(-0,6t). u'v+v'u = exp(-0,6t)-0,6t exp(-0,6t) = (1-0,6t) exp(-0,6t). Repport dans (E) : (1-0,6t)exp(-0,6t)+0,6t exp(-0,6t)= exp(-0,6t) est vérifié quelque soit t. c. En déduire les solutions de l’équation différentielle (E) sur [0 ; +∞[. f(t) = A exp(-0,6 t)+ t exp(-0,6t) = (A+t) exp(-0,6t).  d. En déduire que pour tout réel t appartenant à l’intervalle [0 ; +∞[, on a : v(t) = (12+ t)e−0,6t . v(t)  est de la forme (A+t) exp(-0,6t) avec v(0)=12. (A+0)e0 =12 ; A = 12. ; 2. Dans cette question, on étudie la fonction v sur [0 ; +∞[. a. Montrer que pour tout réel t ∈ [0 ; +∞[, v ′ (t) = (−6,2−0,6t)e−0,6t . On pose u = 12+t et v = exp(-0,6t) ; u' = 1 ; v' = -0,6 exp(-0,6t). u'v+v'u = exp(-0,6t) -0,6(12+t)exp(-0,6t)=exp(-0,6t) ( -6,2-0,6t). b. En admettant que : v(t) = 12e−0,6t + 1 / 0,6 × 0,6t /e 0,6t , déterminer la limite de v en +∞. e−0,6t  tend vers zéro ; par croissance comparée 0,6t /e 0,6t tend vers zéro. Par somme des limites, v(t) tend vers zéro. c. Étudier le sens de variation de la fonction v et dresser son tableau de variation complet. Justifier.  d. Montrer que l’équation v(t) = 1 admet une solution unique a, dont on donnera une valeur approchée au dixième. la fonction v est continue car dérivable et strictement décroissante de 12 à 0 sur l'intervalle [0 ; +oo[. 1 appartient à ]0 ; 12], d'après le théorème des valeurs intermédiaires, il existe un réel unique a tel que v(a) =1. v(4,6) = 1,05 ; v(4,7) = 0,995 ; a ~4,7.  3. Lorsque la vitesse du chariot est inférieure ou égale à 1 mètre par seconde, un système mécanique se déclenche permettant son arrêt complet. Déterminer au bout de combien de temps ce système entre en action. Justifier. La vitesse est inférieure à 1 m/s au bout de 4,7 s. Le dispositif d'arrêt se déclenche au bout de 4,7 s. Partie C. On admet que pour tout réel t dans l’intervalle [0 ; +∞[ :  1. À l’aide d’une intégration par parties, montrer que la distance parcourue par le chariot entre les instants 0 et t est donnée par : d(t) = e −0,6t ( − 5 /3 t − 205 /9 ) + 205 /9 . v(t) = (12+ t)e−0,6t . On pose u =12+ t et v' = exp(-0,6t) ; u' = 1 ; v= -1/0,6 exp(-0,6t). Remarque : 1 / 0,6 = 10 / 6 = 5 / 3. 1/0,36 = 100 / 36 = 25 / 9.   2. On rappelle que le dispositif d’arrêt se déclenche lorsque la vitesse du chariot est inférieure ou égale à 1 mètre par seconde. Déterminer, selon ce modèle, une valeur approchée au centième de la distance parcourue par le chariot dans la zone de freinage avant le déclenchement de ce dispositif. t = 4,7 s. d(4,7) = (-205 / 9 -5*4,7 /3) exp(-0,6 x4,7) +205 / 9 = - 30,6 *0,0596 +22,77 ~ 21 m.

menu