On munit l’espace d’un repère orthonormé.
1. On considère les points A(−1 ; 0 ; 5) et B(3 ; 2 ; −1).
Affirmation 1 : Une représentation paramétrique de la droite (AB) est :
x = 3−2t
; y = 2− t;
z = −1+3t
avec t réel.
Le point B de coordonnées (3 ; 2 ; -1) appartient à la droite (AB).
Coordonnées du vecteur unitaire de la droite (AB) : (-2 ;-1 ;3.
Affirmation vraie.
Affirmation 2 : Le vecteur n de coordonnées (5 ; -2 ; 1) est normal au plan (OAB).
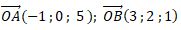
Ces deux vecteurs non colinéaires définissent le plan (OAB).
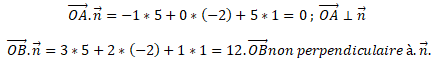Affirmation fausse.
On considère :
la droite d de représentation paramétrique
x = 15+ k ; y = 8− k
; z = −6+2k avec k réel.
la droite d
′ de représentation paramétrique
x = 1+4s
; y = 2+4s
; z = 1−6s
avec s réel.
Affirmation 3 : Les droites d et d
′ ne sont pas coplanaires.
Les deux droites sont dirigées selon les vecteurs :
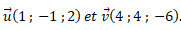
Ces deux vecteurs ne sont pas colinéaires : donc les droites ne sont pas parallèles.
Elles peuvent être sécantes ou non coplanaires.
Existe t-il un couple ( k , s) tel que le point de paramètre k de (d) soit confondu avec le point de paramètre s sur (d').
On va résoudre le système suivant :
15+k = 1+4s soit 14+k=4s ; k = 4s-14.
8-k = 2+4s soit 6-k=4s ; 6-4s+14=4s ; 8s =20 ; s = 2,5. Par suite k = -4.
-6+2k=1-6s ; -6+2(-4) = 1-6*2,5 ; -14 =-14 est vraie.
Solution du système ( k = -4 ; s = 2,5).
Les deux droites sont sécantes et coplanaires.
Affirmation fausse.
On considère le plan P d’équation x − y + z +1 = 0.
Affirmation 4 : La distance du point C(2 ; −1 ; 2) au plan P est égale à 2*
3
½.
Coordonnées dun vecteur n normal au plan (P) : 1 ; -1 ; 1.
Représentation paramétrique de la droite (d) orthogonale au plan P et passant par C :
x = 2+t ; y = -1-t ; z = 2+t avec t réel.
On appelle K le projeté orthogonal de C sur le plan P.
x
K-y
K+z
K+1=0.
2+t-(-1-t)+2+t+1=0.
6+3t =0 ; t = -2.
k(2-2 ;-1-(-2) ; 2-2) soit (0 ; 1 ; 0).
CH
2 = (0-2)
2 +(1-(-1))
2 +(0-2)
2 =4+4+4=12 : CH = 2 *3
½.
Affirmation vraie.
