La physique au service du vigneron. Bac Métropole 09 /2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
L’objectif de cet exercice est d’étudier comment la physique peut être utile au vigneron pour mesurer le niveau de remplissage de la cuve de stockage, contrôler la température du jus de raisin et en déterminer le taux de sucre au cours de la fermentation.
1. Étude du principe du capteur de niveau.
 La cuve de stockage est équipée d’un capteur de niveau de type capacitif permettant de contrôler la hauteur de liquide.
Ce capteur est constitué d’une tige conductrice recouverte d’une très fine couche d’isolant. Lorsque celle-ci trempe dans un liquide conducteur, comme le jus de raisin, elle constitue une des armatures d’un condensateur et le liquide en constitue l’autre. On considère pour simplifier que l’ensemble se comporte comme un condensateur plan. 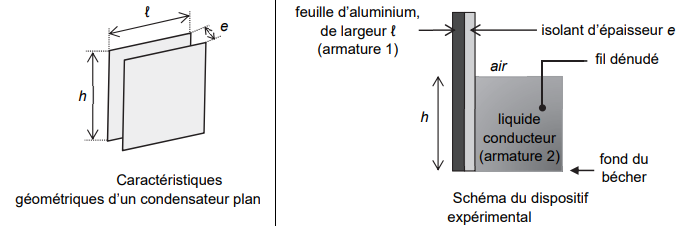On souhaite étudier en laboratoire le principe de ce capteur et l’influence de la hauteur de liquide sur le comportement d’un tel condensateur en réalisant le montage représenté :
- une feuille d’aluminium rectangulaire de largeur l = 41 cm constitue l’armature 1 du condensateur ;
 - une feuille plastifiée d’épaisseur e = 80 µm de polyester joue le rôle d’isolant ;
- la plaque, formée par la feuille d’aluminium et la feuille plastifiée, est plongée dans un récipient et en touche le fond. Elle est en contact sur une hauteur h avec un liquide conducteur qui joue le rôle de l’armature 2 du condensateur ;
- un fil dénudé permet d’établir un contact électrique avec le liquide.

la surface SC de chaque armature du dispositif expérimental s’exprime par la relation : SC = h·l ;
 la capacité C du condensateur plan de ce dispositif s’exprime par la relation : C = e SC / e  avec C en farad (F), SC en m2, e en m et e, grandeur caractéristique de l’isolant appelée permittivité, exprimée en F·m–1.
Q1. Expliquer pourquoi ce capteur ne peut pas être utilisé dans un liquide isolant
La seconde armature du condensateur est constituée par le liquide. Cette armature ( donc le liquide) doit être conductrice.
 Q2. Préciser si la capacité C du condensateur augmente ou diminue lorsque la hauteur h de liquide dans lequel l’ensemble est plongé augmente.
Si  h augmente, SC croît et en conséquence la capacité C augmente.
 Pour mesurer la valeur de la capacité du condensateur, on réalise le circuit électrique représenté ci-dessous. Il comporte :
 - un générateur idéal de tension E = 5,0 V ;
- un conducteur ohmique de résistance R = 6,0×106 ohms ;
 - le dispositif expérimental ci-dessus jouant le rôle d’un condensateur de capacité C ;
- un interrupteur à deux positions.

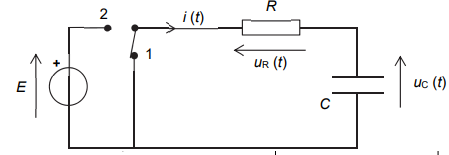
L’interrupteur est préalablement placé en position 1 afin de décharger le condensateur. À l’instant t = 0, le condensateur est déchargé et l’interrupteur est basculé en position 2.
Q3. Montrer que, lors de sa charge, la tension uC(t) aux bornes du condensateur obéit à l’équation différentielle suivante : Additivité des tensions : UR(t) +UC(t) = E.
Ri(t) +UC(t) = E.
i(t) = C dUC(t) / dt.
RC dUC(t) / dt +UC(t) = E.
dUC(t) / dt +UC(t) / (RC)= E / (RC).
Q4. La tension d’expression uC(t)= A·exp(– t / t) + B est solution de cette équation différentielle. Déterminer, en fonction des paramètres E, R et C, les expressions des constantes A, B et t adaptées aux conditions de l’expérience.
t = RC.
Au bout d'un temps suffisamment long uC(t) = E =0+B.
u(t=0)=0= A +B ; A = -B = -E.
uC(t) = E(1-exp(– t / t)).
 On réalise une première expérience de charge du condensateur pour une hauteur htest de liquide. La figure ci-dessous représente l’évolution temporelle de la tension uC(t) aux bornes de ce condensateur.

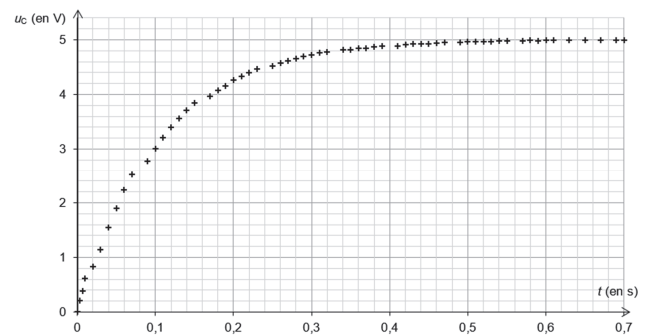
Au bout de 0,5 s, uC(t) = E.
5t= 0,5 ; t = 0,1 = RC.
C = 0,1 / (6,0 106)~1,67 10-8 F.
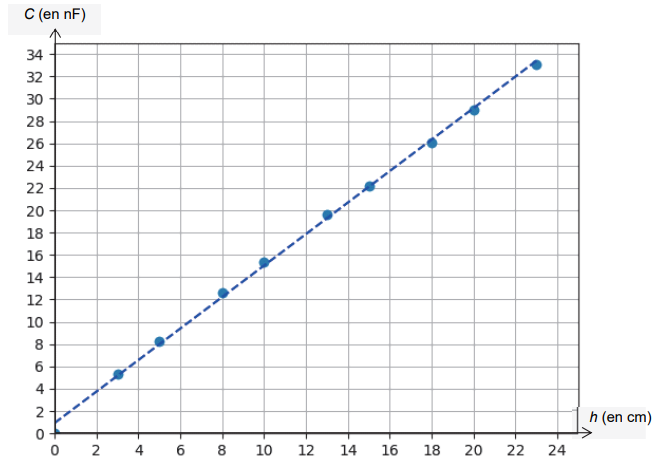
L’expérience est reproduite pour différentes hauteurs h de liquide. La représentation graphique de la variation de la capacité du condensateur en fonction de la hauteur de liquide est donnée. Une droite de modélisation y a été tracée.

Q5. À l’aide des figures, déterminer la hauteur htest de liquide utilisée dans la première expérience.
Coefficient directeur de la droite : (33-1) / 23 ~1,4 nF cm-1= 1,4 10-9 F cm-1.
Equation de la droite : C = 1,4 10-9h +1.
1,67 10-8=1,4 10-9 htest+1 ; htest= 1,67 / 0,14 -1~ 11 cm.

... =  =
....

 2. Contrôle de la température du jus de raisin.
 Pour que la fermentation alcoolique se produise, la température du jus doit être maintenue autour de 18°C. Ainsi, la cuve de stockage est équipée d’un échangeur thermique plongeant dans le jus permettant d’assurer soit un chauffage soit un refroidissement du jus, en fonction des variations constatées de la température de celui-ci. On souhaite établir le bilan énergétique du système {jus de raisin} afin de déterminer la puissance de l’échangeur thermique à utiliser. La figure ci-dessous présente les puissances échangées entre le système {jus de raisin} et le milieu extérieur. On considère que le jus de raisin est à l’équilibre thermique.

- température du jus à maintenir lors de la fermentation alcoolique : qjus = 18 °C ;
 - température moyenne de l’air extérieur : qext = 22 °C ;
 - caractéristiques de la cuve de stockage :  contenance : V = 2 m3 ;  surface d’échange thermique : S = 9 m2 ;
- la capacité thermique de l’ensemble du jus de raisin est notée CJ (en J·K–1) ;
-la fermentation d’une masse de jus mjus dégage une puissance thermique PF donnée par une loi empirique : PF = 0,127 · mjus où mjus est en kg et PF en W ;
-  flux thermique entre l’extérieur et l’intérieur de la cuve de stockage : FP = A·S·(qext – qjus) avec :  S la surface d’échange thermique (en m2) ;  A le coefficient global d’échange par les parois de la cuve de stockage : A = 12 W·m–2·K–1 ;
- masse volumique du jus de raisin au cours de la fermentation alcoolique : rjus = 1 090 kg·m–3.
Q6. Indiquer, en justifiant, le sens du transfert thermique s’opérant entre le jus maintenu à la température qjus et l’air extérieur à la température qext lors de la fermentation alcoolique.
Le transfert s'effectue du corps le plus chaud ( l'air extérieur 22°C) vers le corps le plus froid ( le jus 18°C).
Q7. Calculer la valeur du flux thermique global FP à travers les parois de la cuve de stockage.
FP = A·S·(qext – qjus)=12 x 9 x(22-18)=432 W.
 Q8. Calculer la puissance PF dégagée par la fermentation du jus de raisin dans la cuve de stockage entièrement remplie.
PF =0,127 x2 x1090=276,86 ~277 W.
 On admet que, compte tenu du dégagement d’énergie lié à la fermentation, le premier principe de la thermodynamique appliqué au système fermé {jus de raisin}, dont la température varie de Dq entre deux instants t et t+Dt, conduit à la relation ci-dessous :
 CJ·Dq = (FP + P+ PF)·Dt
Q9. Déterminer la valeur de la puissance thermique P de l’échangeur interne placé dans la cuve de stockage permettant de maintenir constante la température du jus. Interpréter le signe de P.
A l'équilibre thermique : FP + P+ PF= 0.
P = -432-277= - 709 W.
L'échangeur doit refroidir le jus de raisin.

3. Contrôle du taux de sucre dans le jus de raisin et principe du mustimètre
La mesure de la teneur en sucre d’un jus de raisin permet au vigneron de suivre au cours du temps le processus de fermentation. Lorsque la teneur en sucre est stabilisée à son minimum, l’étape de fermentation alcoolique est terminée. Pour cela, le vigneron utilise un mustimètre, appareil qui mesure la masse volumique rjus du jus. Cette mesure permet ensuite de connaître la concentration en masse de sucre. On étudie dans cette partie le principe de fonctionnement d’un mustimètre.
Données : - la poussée d’Archimède est la force exercée par un fluide sur un système immergé dans ce fluide. Ses caractéristiques sont :
 direction : verticale ;  sens : vers le haut ;  valeur : F = r·V·g où r est la masse volumique du fluide, V est le volume de la partie immergée du système et g est l’intensité de la pesanteur ;
 - le mustimètre étudié, de masse m0 = 55 g, est composé de deux parties :  un tube large, totalement immergé, de volume V0 = 49 mL ;  un tube fin gradué, de forme cylindrique, partiellement immergé, de section ST = 5×10–5 m2 ; on note hT la hauteur immergée du tube ;
 on néglige la poussée d’Archimède due à l’air devant celle exercée par le jus de raisin. Pour réaliser la mesure, le mustimètre est plongé dans un échantillon de jus de raisin, flotte et se stabilise : on peut alors lire la masse volumique sur le tube fin gradué .

Q10. Identifier les deux forces agissant sur le système {mustimètre} en équilibre dans le jus de raisin.
Poids, verticale, vers le bas, valeur mg.
Poussée d'Archimède F.
 Q11. Montrer que la hauteur hT de la partie immergée du tube fin peut s’écrire sous la forme : hT = m0 / (rjus ST) -V0 / ST.
Poids = m0g.
Poussée F = (V0 +hTST)rjus g.
A l'équilibre : m0 = (V0 +hTST)rjus  ; m0 / rjus=V0 +hTST.
(m0 / rjus-V0 ) / ST = hT.
 Q12. Les graduations sur le tube fin du mustimètre indiquent la valeur de la masse volumique du liquide, exprimée en g·mL–1. Justifier qualitativement que le mustimètre s’enfonce lorsque la masse volumique du jus diminue.
Si la masse volumique du jus diminue, la poussée d'Archimède, verticale vers le haut, diminue alors que le poids du mustimètre reste constant. Le mustimètre s'enfonce.
La plage de mesure du mustimètre correspond à une hauteur hT immergée variant entre 1 cm et 14 cm.
Q13. Déterminer la masse volumique minimale rjus,min que peut mesurer ce mustimètre.
hT = m0 / (rjus ST) -V0 / ST = 0,14.
0,14= 0,055 /(5 10-5 rjus,min )- 49 10-6 /(5 10-5) ;
0,14 +0,98 =1100 / rjus,min ;
rjus,min =1100 /  1,12 ~982 kg m-3.
Q14. La masse volumique du jus de raisin diminue lorsque le degré de fermentation augmente. Expliquer le problème que l’on rencontre lors de l’utilisation de ce mustimètre avec un jus trop fermenté. 
Le jus contient trop d'alcool et donc sa masse volumique diminue : le mustimètre s'enfonce trop et la lecture devient impossible.



  
menu