Mathématiques. Probabilités. Bac
Polynésie 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Une équipe américaine a cartographié pour la première fois les allergies alimentaires chez
l’enfant aux États-Unis en 2020. L’étude, publiée dans la revue Clinical Pediatries, révèle
une différence nette entre les zones rurales et les zones urbaines.
On sait qu’en 2020, 17 % de la population des États-Unis habite en zone rurale et 83 % en
zone urbaine.
L’étude menée montre que parmi les enfants des États-Unis vivant en zone rurale, il y en a
6,2 % qui sont atteints d’allergie alimentaire.
L’étude révèle aussi que 9 % des enfants des États-Unis sont atteints d’allergie alimentaire.
Sauf mention contraire, les probabilités seront données sous forme exacte.
Partie A
On interroge au hasard un enfant dans la population des États-Unis et on note :
R L’évènement : « l’enfant interrogé habite en zone rurale »;
A L’évènement : « l’enfant interrogé est atteint d’allergie alimentaire ».
1. Traduire cette situation à l’aide d’un arbre de probabilité.
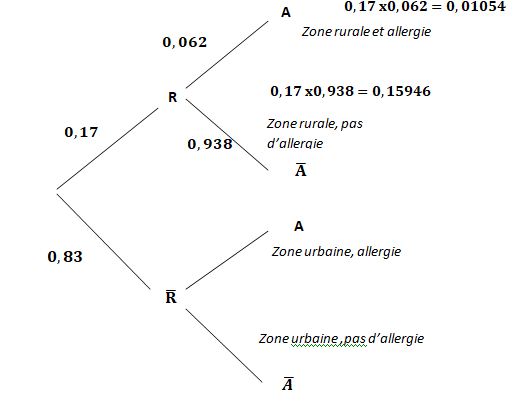 2. a.
2. a. Calculer la probabilité que l’enfant interrogé habite en zone rurale et soit atteint
d’allergie alimentaire.
P(R n A)=P(R) x P R(A) = 0,17 * 0,062 =0,01054.
b. En déduire la probabilité que l’enfant interrogé habite en zone urbaine et soit
atteint d’allergie alimentaire.
P(A) = P(R n A) +P(non R n A) = 0,09.
P(non R n A) =0,09-0,01054=0,07946.
c. L’enfant
interrogé habite en zone urbaine. Quelle est la probabilité qu’il soit
atteint d’allergie alimentaire ? Arrondir le résultat à 10 −4
.
P non R(A) = P(non R n A) / P(non R) = 0,007946 / 0,83~0,09573.
Partie B
On réalise une étude en interrogeant au hasard 100 enfants des États-Unis.
On admet que ce choix se ramène à des tirages successifs indépendants avec remise.
On note X la variable aléatoire donnant le nombre d’enfants atteints d’allergie alimentaire
dans l’échantillon considéré.
1. Justifier que la variable aléatoire X suit une loi binomiale dont on précisera les paramètres.
On répète 100 fois de manière identique et indépendante un expérience aléatoire présentant deux issues :
succès = l'enfant est atteint d'une allergie alimentaire p = ,09.
X compte le nombre de succcès. X suit la loi binomiale de paramètres n = 100 ; p = 0,09
2. Quelle est la
probabilité qu’au moins 10 enfants parmi les 100 interrogés soient
atteints d’allergie alimentaire ? Arrondir le résultat à 10 −4
.
P(X > 10) =0,4125.
Partie C
On s’intéresse à un échantillon de 20 enfants atteints d’allergie alimentaire choisis au hasard.
L’âge d’apparition des premiers symptômes allergiques de ces 20 enfants est modélisé par
les variables aléatoires A 1, A 2,...,, A 20. On admet que ces variables aléatoires sont indépendantes et suivent la même loi d’espérance 4 et de variance 2,25.
On considère la variable aléatoire :
M 20 =
(A 1 + A 2 +...+ A 20
) /20
.
1. Que représente la variable aléatoire M 20 dans le contexte de l’exercice ?
M 20 : âge moyen d'apparition des premiers symptômes de la maladie.
2. Déterminer l’espérance et la variance de M 20.
E(A) = 4 ; V(A) = 2,25.
E(M 20)= 4 ; V(M 20)=V(A)/20=2,25 / 20 = 0,1125.
3. Justifier, à l’aide de l’inégalité de concentration, que
P (2 < M 20 < 6) > 0,97.
Interpréter ce résultat dans le contexte de l’exercice.
|M 20-4| < 2 ; P( |M20-4| < 2 ) = 1- P(|M20-4| > 2 ).
P(|Mn-E(A)| > t) < V(A) / (nt2).
P(|M20-4 > 2|) < 2,25 / (20x22).
P(|M20-4 > 2|) < 2,25 / (20x22)=2,25 /80.
P(|M20-4 |< 2 ) > 1-2,25 / 80 ;
P(|M20-4 |< 2 ) >311 / 320~0,9719.
Dans 97 % des cas, les premiers symptômes apparaissent entre 2 et 6 ans.
|
...
= =
|
....
|
Dans tout l’exercice, les probabilités seront, si nécessaire, arrondies à 10−3
près.
Une donnée binaire est une donnée qui ne peut prendre que deux valeurs
: 0 ou 1.
Une donnée de ce type est transmise successivement d’une machine à une
autre.
Chaque machine transmet la donnée reçue soit de manière fidèle,
c’est-à-dire en transmettant l’information telle qu’elle l’a reçue (1
devient 1 et 0 devient 0), soit de façon
contraire (1 devient 0 et 0 et devient 1).
La transmission est fidèle dans 90 % des cas, et donc contraire dans 10
% des cas.
Dans tout l’exercice, la première machine reçoit toujours la valeur 1.
Partie A
Pour tout entier naturel n > 1, on note :
Vn l’évènement : « la n-ième machine détient la valeur 1 »;
non Vn l’évènement : « la n-ième machine détient la valeur 0 ».
1. a. Recopier et compléter l’arbre de probabilité ci-dessous.
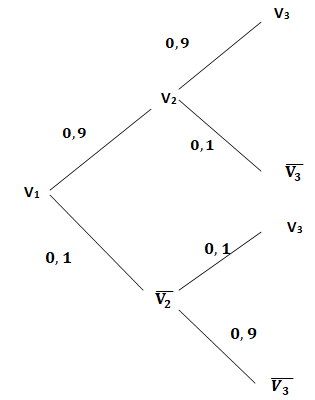
b. Démontrer que P(V3) = 0,82 et interpréter ce résultat dans le contexte de
l’exercice.
Loi des probabilités totales :
P(V3) = P(V3 n V2)+P(V3 n non V2)=0,9 *0,9 +0,1 *0,1=0,82.
c. Sachant que la troisième machine a reçu la valeur 1, calculer la probabilité
que la deuxième machine ait aussi reçu la valeur 1.
PV3(V2)=P(V3 n V2) / P(V3)=0,9 x0,9 / 00,82 =81 / 82 ~0,988.
2. Pour tout entier naturel n > 1, on note pn = P(Vn).
La première machine a reçu la valeur 1, on a donc p1 = 1.
a. Démontrer que pour tout entier naturel n > 1 :
pn+1 = 0,8pn +0,1.
Loi des probabilités totales :
pn+1=P(Vn+1)=P(Vn+1 n Vn)+P(Vn+1 n non Vn)
pn+1=PVn(Vn+1) x P(Vn)+Pnon Vn(Vn+1) x P(non Vn).
pn+1=0,9 *P(Vn)+0,1 *P(non Vn).
pn+1=0,9 pn +0,1(1-pn) =0,8pn+0,1.
b. Démontrer par récurrence que pour tout entier naturel n > 1,
pn = 0,5×0,8n−1 +0,5.
Initialisation : p1=1 et 0,5×0,81−1 +0,5=1.
L'affirmation p1 est vraie.
Hérédité : pn = 0,5×0,8n−1 +0,5 est supposé vraie.
0,8 pn =0,5×0,8n +0,4
0,8 pn +0,1=0,5×0,8n +0,4+0,1.
pn+1=0,5×0,8n +0,5.
L'affirmation est vraie au rang n+1.
Conclusion : l'affirmation est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier naturel n.
c. Calculer la limite de pn lorsque n tend vers l’infini. Interpréter ce résultat
dans le contexte de l’exercice.
-1 < 0,8 < 1 : en plus l'infini 0,8n tend vers zéro.
pn tend vers 0,5.
Partie B
Pour modéliser en langage Python la transmission de la donnée binaire
décrite en début
d’exercice, on considère la fonction simulation qui prend en paramètre
un entier naturel n qui représente le nombre de transmissions réalisées
d’une machine à une autre,
et qui renvoie la liste des valeurs successives de la donnée binaire.
On donne ci-dessous le script incomplet de cette fonction.
On rappelle que l’instruction rand() renvoie un nombre aléatoire de
l’intervalle [0; 1[.
def simulation(n):
donnee = 1
liste = [donnee]
for k in range(n):
if rand() <0.1
donnee = 1 - donnee
liste.append(donnee)
return liste
Par exemple, simulation(3) peut renvoyer [1, 0, 0, 1].Cette liste
traduit : qu’une donnée binaire a été successivement transmise
trois fois entre quatre machines;
la première machine qui détient la valeur 1 a transmis de façon contraire cette
donnée à la deuxième machine;
la deuxième machine a transmis la donnée qu’elle détient de façon fidèle à la troisième;
la troisième machine a transmis de façon contraire la donnée qu’elle détient à la
quatrième.
1. Déterminer le rôle des instructions :
if rand() <0.1
L'instruction de la ligne suivante ne s'excécute que si le test rand() <0.1 renvoie la valeur true.
donnee = 1 - donnee .
Cette ligne modifie la donnée, simulant une transmission contraire.
2. Calculer la
probabilité que simulation(4) renvoie la liste [1, 1, 1, 1, 1] et la
probabilité que simulation(6) renvoie la liste [1, 0, 1, 0, 0, 1, 1].
simulation(4) : on a 4 transmissions fidèles entre 5 machines.
Cette probabilité est égale à : 0,94 ~0,656.
simulation(6) : on a 6 transmissions entre 7 machines.
Les trois premières transmissions sont contraires, la quatrième et fidèle, la cinquième est contraire et la sixième est fidèle.
Cette probabilité est égale à : 0,1 x0,1 x0,1 x0,9 x0,1 x0,9 = 0,92 x0,14 = 8,1 10-5 ~0,00.
|
|
|
|