Mathématiques. Fonctions, suites. Bac Polynésie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
On munit le plan d’un repère orthonormé. Pour tout entier naturel n, on considère la fonction fn définie sur [0 ; +∞[ par :
f0(x) = e −x et, pour n > 1, fn(x) = x n e −x . Pour tout entier naturel n, on note Cn la courbe représentative de la fonction fn. Les parties A et B sont indépendantes.
Partie A : Étude des fonctions fn pour n > 1
On considère un entier naturel n > 1.
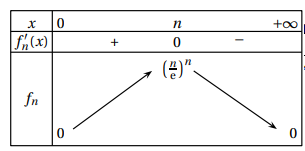
 1. a. On admet que la fonction fn est dérivable sur [0 ; +∞[. Montrer que pour tout x > 0, f ′ n (x) = (n − x)x n−1 e −x .
On pose u = xn et v = e-x ; u' = n xn-1 ; v' =-e-x ;
u'v+v'u = n xn-1e-x -xn e-x =xn-1e-x (n-x).
b. Justifier tous les éléments du tableau ci-dessous :

f ′ n (x) >0 si x < n et fn(x) est strictement croissante.
f ′ n (x) < 0 si x > n et fn(x) est strictement décroissante.
f ′ n (x) 0 0 si x = n et fn(x) présente un maximum égal à (n/e)n..
Si x tend vers +oo, e-x tend vers zéro et fn(x) tend vers zéro.
Si x tend vers zéro e-x tend vers 1 et xn tend vers zéro ; par produit des limites  fn(x) tend vers zéro.
2. Justifier par le calcul que le point A( 1 ; e−1 ) appartient à la courbe Cn.
fn(1) = 1n e −1 = e-1.
 Partie B : Étude des intégrales.
 Dans cette partie, on étudie les fonctions fn sur [0;1] et on considère la suite (In) définie pour tout entier naturel n par : In
1. On a représenté les courbes C0,C1,C2,C10 et C100.

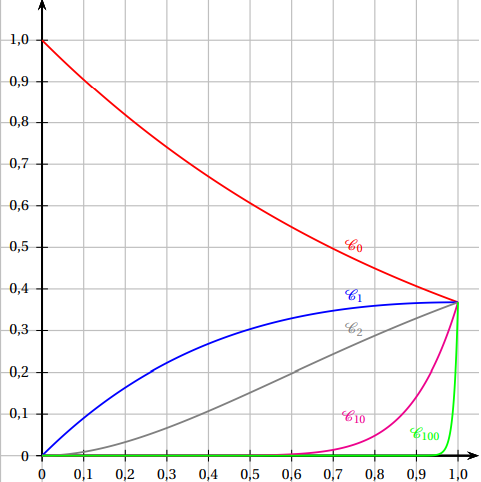a. Donner une interprétation graphique de In.
In représente l'aire du domaine compris entre la courbe Cn, l'axe des abscisses et les droites d'équation x= 0 et x = 1.
b. Par lecture de ce graphique, quelle conjecture peut-on émettre sur la limite de la suite (In) ?
In tend vers zéro si n tend vers l'infini : la suite est décroissante et bornée par zéro.
 2. Calculer I0.
f0(x) = x0 e-x= e-x.
Primitive de e-x : -e-x.
I0 =[ -e-x]01 = -e-1+e0 =1-e-1.
3. a. Soit n un entier naturel. Démontrer que pour tout x appartenant à [0 ; 1], 0 < x n+1 < x n .
0 < x < 1 ;
0 * xn< x * xn< 1 * xn ;
0 < x n+1 < x n .
 b. En déduire que pour tout entier naturel n, on a : 0 < In+1 < In.
0* e-x < x n+1* e-x < x n * e-x.
On intègre entre 0 et 1, par positivité de l'intégrale on déduit :

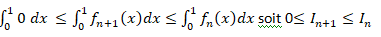
4. Démontrer que la suite (In) est convergente, vers une limite positive ou nulle que l’on notera L.
0 < In , la suite est minorée par zéro.
In+1 < In, la suite est décroissante.
La suite est décroissante et minorée par zéro, donc elle converge vers une limite L.

5. En utilisant une intégration par parties, démontrer que pour tout entier naturel n on a : In+1 = (n +1)In − 1 /e .
On pose u = xn+1 et v' =e-x ; u' = (n+1) xn ; v = -e-x.

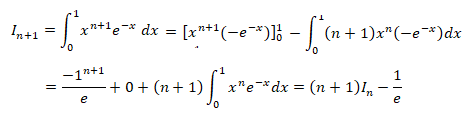 6. a. Démontrer que si L > 0, l’égalité de la question 5 conduit à une contradiction.
On fait l'hypothèse que L >0.
Quand n tend vers +oo : (n+1)In tend vers +oo et donc In+1 tend vers +oo.
Par unicité de la limite la limite en +oo de In est égale à la limite de In+1.
Il y a donc contradiction.
b. Démontrer que L = 0. On pourra utiliser la question 6. a.
D'après la question B 4, on a L > 0 et d'après la question précédente on ne peut pas avoir L >0. Donc L = 0.
On donne ci-dessous le script de la fonction mystere, écrite en langage Python. On a importé la constante e.
def mystere(n):
I = 1 - 1/e
 L = [I]
for i in range(n): I = (i + 1)*I - 1/e
L.append(I)
 return L
7. Que renvoie mystere(100) dans le contexte de l’exercice ?
mystere(100) renvoie la liste des valeurs I0, I1...I100.

... =  =
....

 On considère la fonction f définie sur l’intervalle ]2 ; +∞[ par f (x) = x ln(x −2).
Une partie de la courbe représentative Cf de la fonction f est donnée ci-dessous.

1. Conjecturer, à l’aide du graphique, le sens de variation de f ses limites aux bornes de son ensemble de définition ainsi que les éventuelles asymptotes.
Quand x  tend vers 2, f(x) tend vers -oo ; la droite d'équation x = 2 est asymptote à la courbe Cf.
Quand x tend vers +oo, f(x) tend vers +oo.
f(x) est strictement croissante.
 2. Résoudre l’équation f (x) = 0 sur ]2 ; +∞[.
x ln(x-2) = 0 soit x-2=1 ; x = 3.
3. Calculer la limite de f (x) quand x tend vers 2+. Ce résultat confirme-t-il l’une des conjectures faites à la question 1 ?
ln(x-2) tend vers -oo ; par produit , f(x) tend vers -oo.
 4. Démontrer que pour tout x appartenant à ]2 ; +∞[ : f ′ (x) = ln(x −2)+ x /(x −2).
On pose u = x et v = ln(x-2) ; u' = 1; v' = 1/(x-2).
u'v+v'u = ln(x-2)+ x / (x-2)
 5. On considère la fonction g définie sur l’intervalle ]2 ; +∞[ par g(x) = f ′ (x).
 a. Démontrer que pour tout x appartenant à ]2 ; +∞[, on a : g ′ (x) =(x −4) / (x −2)2
On dérive x / (x-2) en posant u = x et v = x-2 ; u' = v' = 1.
(u'v-v'u) / v2 =(x-2-x) /(x-2)2 =-2 /(x-2)2.
g'(x) = 1/(x-2) -2 /(x-2)2 =(x-2-2) / (x-2)2 =(x −4) / (x −2)2

 b. On admet que la limite de g(x) quand x tend vers 2+ est  +∞ et que g(x) tend vers +oo si x tend vers +oo. En déduire le tableau des variations de la fonction g sur ]2 ; +∞[. On fera apparaître la valeur exacte de l’extremum de la fonction g.

c. En déduire que, pour tout x appartenant à ]2 ; +∞[, g(x) > 0.
g(x) décroit de + oo à 2+ln(2) > 0 puis croît de 2 +ln(2) à +oo.
 d. En déduire le sens de variation de la fonction f sur ]2 ; +∞[.
f '(x) = g(x) >0 ; f(x) est strictement croissante sur cet intervalle.
6. Étudier la convexité de la fonction f sur ]2 ; +∞[ et préciser les coordonnées d’un éventuel point d’inflexion de la courbe représentative de la fonction f .
f "(x) = g'(x).
g'(x) s'annule est change de signe pour x = 4.
Il existe un point d'inflexion de coordonnées (4 ; f(4) =4 ln(2).
Sur ]2 ; 4], g'(x) <0 et f est concave.
Sur [4 ; +oo[ g'(x) >0 et f est convexe
. 7. Combien de valeurs de x existe-t-il pour lesquelles la courbe représentative de f admet une tangente de coefficient directeur égal à 3 ?
f '(x) =g(x) = 3 ;
g(4) = 2+ln(2) ~2,7.
Sur ]2 ; 4], g(x) est strictement décroissante et continue car dérivable ;
3 est compris entre +oo et g(4) ~2,7.
D'après le corollaire du théorème des valeurs intermédiaires, l'équation g(x)=3 admet une solution unique dans ]2 ; 4].
Sur ]4 ; +oo[, g(x) est strictement croissante et continue car dérivable ;
3 est compris entre  g(4) ~2,7 et +oo
D'après le corollaire du théorème des valeurs intermédiaires, l'équation g(x)=3 admet une solution unique dans ]4 ; +oo[.
L'équation f '(x) =g(x)= 3 admet deux solutions.



  
menu