Mathématiques. DNB Polynésie 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . . . .. .. ...... ... Exercice 1 20 points.  L’association sportive d’un collège propose aux élèves une activité escalade. La feuille de calcul ci-dessous obtenue à l’aide d’un tableur indique la répartition par âge des élèves inscrits à l’escalade. A B C D E F G H 1 Age 10 11 12 13 14 15 total 2 Effectif 1 3 8 12 4 2 30 1. Quel est le nombre d’élèves âgés de 12 ans inscrits à l’escalade ? 8 élèves.  2. Calculer le nombre total d’élèves inscrits à l’escalade. 30 élèves. 3. Quelle formule peut-on saisir dans la cellule H2 pour obtenir le nombre total d’élèves inscrits à l’escalade ? =SOMME(B2:G2)  4. Le professeur affirme : « 1 / 5 des élèves inscrits à l’escalade ont 14 ans ou plus ». A-t-il raison ? 6 élèves ont 14 ans ou plus. 6 / 30 =1 /5. Il a raison.  5. L’année dernière, la moyenne des âges des élèves inscrits à l’escalade était de 13 ans. La moyenne des âges des élèves inscrits à l’escalade cette année a-t-elle augmenté par rapport à l’année dernière ? (10+3*11+8*12+13*12+14*4+15*2) / 30 = 12,7. La moyenne des âges a diminué.  6. L’association prévoit une hausse de 10 % des inscriptions à l’escalade l’année prochaine. Déterminer le nombre d’élèves qui seront inscrits à l’escalade l’année prochaine. 30 x1,1 = 33 élèves. Exercice 2. 22 points. Le jardin botanique d’une ville peut être représenté par le quadrilatère ABCD ci-dessous.. 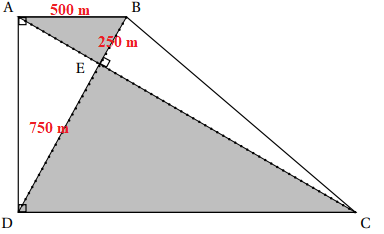1. Quelle est la longueur du segment [DB] ? 250 +750 = 1000 m. 2. En raisonnant dans le triangle rectangle ABD, montrer que la longueur du segment [AD], arrondie au mètre, est égale à environ 866 m. Relation de Pythagore : DB2 = AB2 +AD2. AD2=DB2 - AB2 =10002-5002=750 000 ; AD ~866 m. 3. a. Calculer le sinus de l’angle EAB.  b. En déduire la mesure en degrés de l’angle EAB. sin(EAB) = EB / AB = 250 / 500 = 0,5 ; l'angle mesure 30°.   4. a. Montrer que les droites (AB) et (DC) sont parallèles. Les droites (AB) et (DC) sont perpendiculaires à AD : elles sont donc parallèles. b. Montrer que la longueur du segment [CD] est égale à 1 500 m. Les triangles ABE et CDE sont semblables. CD / AB = DE/ BE ; CD = DE x AB / BE = 750 x500 /250 = 1500 m.  5. Un piéton fait le tour du jardin botanique en marchant à la vitesse moyenne de 1,1 m/s. Il lit sur son plan que la longueur du segment [BC] est environ égale à 1 323 m. Le temps mis par le piéton pour faire le tour du jardin botanique est-il inférieur à une heure ? AB+BC+CD+AD = 500 +1323+1500+866 =4 189 m. 4 189 / 1,1 ~3808 s.. Le temps mis pour faire le tour est supérieur à une heure. Exercice 3 QCM. 20 points. Question 1 (-3)2 = 9. Réponse D. Question 2  La décomposition en produit de facteurs premiers du nombre 360 est 360 = 23x32x5. Réponse D. Question 3 . Un rectangle d’aire 135 cm2 a pour largeur 3 cm. Combien mesure sa longueur ? longueur x largeur = aire du rectangle. 135 / 3 = 45 cm. Réponse B. Question 4 Quelle expression littérale correspond à la longueur du segment [BG] ? 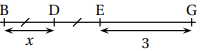BG = BD+DE+EG = x+x+3 = 2x+3.  Réponse D . Question 5 Le rectangle ADCB est partagé en neuf rectangles identiques. 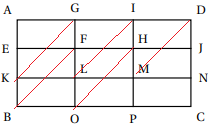L’image du rectangle GFHI par la translation qui transforme D en M est le rectangle KBOL.  . Réponse C. ... =  = .... Exercice 4 20 points   On considère le programme de calcul suivant. 1. Montrer que si on choisit 5 comme nombre de départ, le résultat du programme est 2. 5+4=9 ; 5-2=3 ; 9 x3=27 ; 27-52=2.  2. On choisit x comme nombre de départ. a. Parmi les expressions suivantes, quelle est celle qui permet d’exprimer le résultat de ce programme de calcul en fonction de x ? (x+4) (x-2) -x2. Expression C. b. Montrer que le résultat du programme de calcul peut s’écrire sous la forme 2x−8. (x+4) (x-2) -x2= x2+4x-2x-8 -x2=2x-8.  3. On appelle f la fonction définie par f (x) = 2x −8. Voici trois représentations graphiques : a. La représentation graphique de la fonction f est la représentation n° 3. Expliquer pourquoi les représentations n° 1 et n° 2 ne conviennent pas. La représentation graphique de f(x) = 2x-8 est une droite ne passant pas par l'origine. ( Fonction affine). La représentation 1 ne convient pas. f(-4) = -16 : la représentation 2 ne convient pas. f(4) =2*4-8=0. La représentation 3 convient. b. Déterminer l’image de 4 par la fonction f . f(4) = 2 *4-8 =0. 4. Quel nombre de départ faut-il choisir pour que le résultat du programme de calcul soit égal à 100 ? 100 = 2x-8 ; 100+8=108 = 2x ; x = 1082 /2 = 54. Exercice 5 18 points Partie A Tom a acheté un dé équilibré à 12 faces numérotées de 1 à 12. Il lance ce dé et s’intéresse au résultat qui apparaît sur la face du dessus. Le résultat obtenu est 3. 1. Expliquer pourquoi la probabilité d’obtenir le nombre 4 est égale à 1 /12 . Une seule face porte le n° 4. Le dé compte 12 faces numérotées de 1 à 12. Probabilité d'obtenir 4 = 1 / 12. 2. Quelle est la probabilité que le résultat obtenu soit un nombre pair ? 2 ; 4 ; 6 ; 8 ; 10 ; 12 soit 6 possibilités sur 12. Probabilité d'obtenir un nombre pair : 6 /12 = 0,5. 3. Tom pense que la probabilité d’obtenir un multiple de 3 est supérieure à 0,3. A-t-il raison ? Les multiples de 3 sont : 3 ; 6 ; 9 et 12. Probabilité d’obtenir un multiple de 3 = 4 /12 = 1/3 ~0,33. Il a raison. Partie B Tom souhaite maintenant simuler le lancer de deux dés équilibrés à 12 faces numérotées de 1 à 12. Le bloc « lancer » simule le lancer des deux dés et calcule la somme obtenue. Par exemple, si le résultat du dé no 1 est égal à 3 et que le résultat du dé no 2 est égal à 5 alors la somme sera égale à 8. Voici le programme de Tom. 1. Recopier les lignes 2, 3 et 4 du bloc « Lancer » en les complétant. 2. Si le résultat du dé n° 1 est égal à 8 et le résultat du dé n° 2 est égal à 3, qu’affichera le programme ? Justifier. Résultat = Dé1 +Dé2 = 8+3=11. Cette valeur étant supérieure à 6, le programme  dit "gagné" pendant 2 secondes.

menu