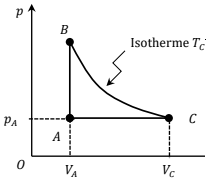
Capacités thermiques d'un gaz parfait, concours Ecole Nationale de l'Aviation Civile 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... On considère n moles d'un gaz parfait décrivant le cycle : A --> B : compression isochore de volume VA. B --> C : détente isotherme à la température TB = TC. C --> A : compression isobare à la pression PC = PA. Température à l'état A : TA ; volume à l'état C : VC. DT = TC-TA ; DV = VC-VA ; 19. Quelle est la variation d'énergie interne du gaz lors de la transformation A --> B ? DUAB =CV(TB-TA)= CV(TC-TA)=CV DT.   Réponse C. 20. Quel est le travail WBC reçu par le gaz lors de la transformation B--> C ? Les transformations étant supposées réversibles  ( quasi-statiques) : P = Pext. . 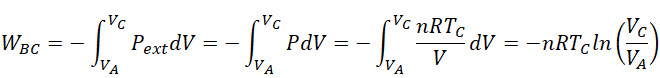Réponse A. 21. Exprimer le travail précédent en fonction de PA, VA, TA, DT et DV. VC= DV+VA ; VC / VA = 1+DV / VA ; nRTC =PCVC =  PAVC  car C--> A est une isobare. nRTC =PA VA VC / VA ; TA / VA = PA / (nR) =PC / (nR) =TC / VC =(DT+TA) / TA =1+DT / TA. WBC= -PA VA(1+DT / TA) ln(1+DV / VA). Réponse B. 22. Que vaut le transfert thermique QBC reçu par le gaz lors de la transformation BC ? On note DUBC la variation d'énergie interne du gaz au cours de cette transformation. La transformation B --> C est isotherme : DUBC = 0. QBC+WBC = 0. Réponse B. 23. Exprimer QCA et WCA lors de la transformation CA. La transformation C --> A est isobare. QCA = DHCA = CP(TA-TC)= -CPDT. 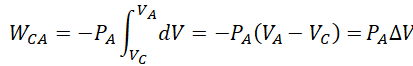Réponses B et C. 24. Déterminer l'expression de DV/ DT en fonction de VA et TA puis en écrivant le bilan d'énergie interne sur le cycle, en déduire la relation entre CP et CV. DV / VA = VC / VA-1  ; DT / TA = TC / TA-1  =VC / VA-1=DV / VA. DV / DT =VA/ TA. Relation entre les capacités thermiques d'un gaz parfait  : CP-CV = nR ( relation de Mayer) CP-CV =PAVA / TA =PADV / DT. Réponses B et C.

menu