Mathématiques.  Concours ESA 2025.
Ecole de santé des armées

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.. . .

.
.
.. ..
......


...
Exercice 1. 6 points
QCM 1. On considère la fonction f définie sur R par f (x) =(ex-2) / (ex+2).
Alors pour tout réel x, f '(x) est égale à :
On pose u = ex-2 et v = ex+2.
u' = v' = ex.
(u'v-v'u) / v2 = ex((ex+2)-(ex-2)) / (ex+2)2 = 4ex / (ex+2)2 ; réponse A.

QCM 2. La limite en +oo de A =4x-3ln(x) est égale à :
A =x ( 4 -3ln(x) / x ).
Par croissance comparée : ln(x) / x tend vers zéro si x tend vers +oo.
A tend vers +oo. Réponse A.

QCM 3 On considère la fonction f définie sur R par f (x) = x 3  / (x4+2). Une primitive de f sur R est la fonction F définie pour tout réel x par :
On pose u = x4+2 ; u' = 4x3.
f(u) = 0,25 u' / u.
F = 0,25 ln(u) =0,25 ln(x4+2). Réponse B.

QCM 4 Le nombre de solutions réelles de l’équation exp(1 /x) = 1 / exp(x) est :
exp(1/x) * exp(x) = 1.
exp(1 /x +x) = 1.
1/x +x= ln(1) = 0.
1 /x = -x ;
x2=-1. Aucune solution réelle. Réponse C.

QCM 5 Le nombre de solutions réelles de l’équation ln (x2) = (ln(x)) 2 est :
2 ln(x) = (ln(x))2.
On pose X = ln(x) ;
2 X = X2.
X2-2X =0.
X(X-2) =0.
Solutions X = 0 et X = 2.
ln(x) =0 soit x =1 ; ln(x) =2 soit x = e2. Réponse A.

QCM 6 Une promotion de 50 étudiants doit élire deux délégués. Le nombre de possibilités est :
(50 2)=50 * 49 / 2 = 1225. Réponse C.

Exercice 2. 6 points.
QCM 7Le quart d’une population a été vacciné contre une maladie contagieuse. Dans cette population, au cours d’une épidémie de cette maladie, on constate qu’il y a, parmi les malades, une personne vaccinée pour quatre non vaccinées et aussi un malade sur douze parmi les personnes vaccinées. Dans cette population, la probabilité de tomber malade est :

On appelle  les événements :
V : la personne est vaccinée
M : la personne est malade.
Probabilité de choisir une personne vaccinée : P(V) = 0,25.
Probabilité de choisir une personne vaccinée parmi les malades : PM(V) = 1 /5 = 0,2.
Probabilité de choisir un malade parmi les vaccinés : PV(M) = 1 /12.
P(V n M) = P(V) x PV(M) = 1 /4 x 1/12 = 1 /48.
PM(V) = P(V n M) / P(M) =1 /5 .
P(M) =5 P(V n M) = 5 /48. Réponse B.

QCM 8À l’épreuve de mathématiques du concours d’entrée à l’Ecole de Santé des Armées, les candidats sont sélectionnés en répondant à 10 questions. Pour chaque question, ils doivent choisir la bonne réponse parmi quatre affirmations dont une seule est exacte. Un candidat se présente et répond à toutes les questions au hasard. La probabilité qu’il ait au moins 9 réponses exactes est égale à :
On note X la variable aléatoire donnant le nombre de bonnes réponses aux 10 questions. X suit la loi binomiale de paramètres n = 10 et p = 1 /4.
P(X >9) = P(X=9 )+ P(X) =10.
P(X=9) = (10 9) * 0,259 *0,751=10 *0,259 *3 /4= 30 /410.
P(X=10) = (10 10) * 0,2510 *0,750=1 *0,2510 *1= 1 /410.
P(X >9)=(30 +1)/ 410. Réponse C.

QCM 9. Si une fonction f définie sur R vérifie : x+2 < f (x) pour tout réel x, alors on peut déterminer la limite de la fonction f lorsque x tend vers :
La limite de x+2 quand x  tens vers +oo est +oo.
Si x+2 < f(x)  d'après les théorèmes de comparaison f(x) tend vers +oo si x tend vers +oo.
Réponse D.

QCM 10 On considère une suite réelle (un) strictement croissante de premier terme u0 = 1. La suite (vn) est définie pour tout entier naturel n par vn = −1 / (1+3un) . Alors la suite (vn) est :
vn+1-vn=−1 / (1+3un+1) +1 / (1+3un)=(-1-3un+1+3un+1) / ((1+3un+1)(1+3un))=3(un+1-un) / ((1+3un+1)(1+3un)).
La suite (un) étant strictement croissante : un+1-un > 0.
De plus u0 = 1 >0 et la suite (un) est croissante : tous les termes de (un) sont supérieurs à 1, donc positifs..
Donc vn+1-vn > 0 ; (vn) est croissante. Réponse A.

On considère deux évènements A et B, d’événements contraires non A et non B tels que Pnon B (non A) = 0,2 et P(A) = P (non B) = 0,6. Alors la probabilité P (non A ∩B ) est égale à :
Formule des probabilités totales :
P(non A n B) + P(non A n non B) = P(non A).
P(A) = 0,6 ; donc P(non A) = 1-0,6 = 0,4.
P(non A n non B) = P(non B) x Pnon B (non A) = 0,6 x0,2 = 0,12.
Donc P(non A n B) +0,12=0,4.
 P(non A n B )=0,4 -0,12 = 0,28. Réponse B.

QCM 12. L'intégrale suivante est égale à :

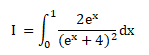
On pose u = (ex+4) ; u' = ex.
Primitive de u'(x) / u(x)2 = -1/u(x) = -1 /(ex+4).
I = 2[-1 /(ex+4)]01=-2/(e1+4)+2/(e0+4) = -2 /(e+4) +2 /5. Réponse C.

... =  =
....
EXERCICE 3 (8 points)
Partie A : Équation différentielle On donne : e = 2,71...; e2 = 7,38...; e3 = 20,08...
On considère l’équation différentielle (E) : y ′ + y = e −x .
1. Montrer que la fonction u, définie pour tout x réel par u(x) = xe −x , est une solution de l’équation différentielle (E).
Calcul de u'(x) en posant v = x et w = e-x.
v' = 1 ; w' = -e-x.
v' w +v w' = e-x-xe-x=(1-x)e-x.
Repport dans (E): (1-x)e-x +xe-x = e-x est vérifié quelque soit x.
2. Résoudre l’équation différentielle (E0) : y ′ + y = 0.
y = A e-x avec A une constante réelle.
3. En déduire les solutions de l’équation différentielle (E).
Somme de la solution générale de l'équation sans second membre et d'une solution particulière de (E) :
y = A e-x +xe −x ,
 4. Déterminer la fonction g solution de (E) qui vérifie g(0) = 2.
2 = A e-0 +0 * e −0 = A.
g(x) = 2 e-x +xe −x .

 Partie B : Étude mathématique d’une fonction.
 On considère la fonction f définie pour tout x réel par : f (x) = (x +2)e−x .
1. a. Dresser le tableau de variation complet de la fonction f en précisant les extremums éventuels.
Calcul de f '(x) en posant u = x+2 et v = e-x.
u' =1 ; v' = -e-x.
u'v+v'u =e-x -(x+2)e-x= -(x+1)e-x.
La dérivée a le signe de -(x+1).

b. Justifier que pour tout x > 1, on a f (x) < 1,2.
f(1)=3e-1 ~ 3 / 2,71 ~1,1 < 1,2.
Sur ]1 ; +oo[, f(x) est strictement dcroissante
Donc pour x >1, f(x) < 1,2.
2. La courbe représentative de la fonction f possède-t-elle un point d’inflexion ? Le cas échéant, préciser ses coordonnées.
Calcul de la dérivée seconde en posant :
u = -(x+1) et v = e-x.
u' = -1 ; v' = -e-x.
u'v-v'u = -e-x +(x+1)e-x =xe-x.
La dérivée seconde s'annule et change de signe pour x =0.
Donc il existe un point d'infexion de coordonnées ( 0 ; 2).
 3. Donner une allure de la représentation graphique de la fonction f dans un repère orthonormé.

 4. a. Déterminer les réels a et b tels que la fonction h : h(x)= (ax +b)e −x soit une primitive de la fonction f sur R.
Calcul de h'(x) en posant u = ax+b et v = e-x.
u' = a ; v' = -e-x.
u'v+v'u = ae-x -(ax+b)e-x =(a-b-ax)e-x= (x+2)e-x.
a = -1 ; a-b=2 ; b = -3.
h(x) = (-x-3)e-x.
b. Calculer l'intégrale . En donner une interprétation graphique.
I = h(2)-h(0) =(-2-3)e-2 +3e-0 =3-5e-2.
I représente l'aire hachurée ci-dessus ( en unité d'aire ).

Partie C : Étude biostatistique
Une patiente, atteinte d’une récidive du cancer du sein, se voit proposer un Pet Scan afin de mettre en évidence les cellules cancéreuses. On lui injecte un traceur (Fluor 18) rendant les cellules cancéreuses colorées et donc visibles à l’imagerie. À la date t = 0, on injecte le traceur dans le corps de la patiente. Le niveau de radioactivité N(t), en MBq (mégabecquerel), dans le corps de la patiente est donné, en fonction du temps t, en heure, par : N(t) = 100 f (t), où f est la fonction étudiée dans la partie B.
 1. Déterminer un encadrement à l’unité de la demi-vie du traceur, c’est-à-dire l’instant auquel le niveau de radioactivité dans le corps de la patiente est la moitié de sa valeur initiale.
N(t) = 100 (t +2)e−t .
N(t½) = 0,5 N(t=0)=0,5 x200 = 100.
100 (t½ +2)e−t½ =100.
 (t½ +2)e−t½ =1
f(1)=3e-1 =3 / e ~1,1.
f(2)=4 e-2=4 /e2~0,54.
1 < t½ < 2 heures.
2. Quel est le niveau moyen de radioactivité dans le corps entre l’instant initial et 2 heures ?
Nmoyen = 100 / 2 (h(2) -h(0)).
h(x) = (-x-3)e-x.
h(2) = (-2-3)e-2~ -5 / 7,38 ~-0,68.
h(0) = -3.
Nmoyen =50(3-0,68)~116 MBq.

 3. On considère que le niveau de radioactivité dans le corps de la patiente est insignifiant lorsqu’il est inférieur à 120 MBq. Est-ce le cas une heure après l’injection ?
N(1) = 100 f(1) =100 *3e-1~110 MBq < 120 MBq.
Le niveau de radioactivité dans le corps de la patiente est insignifiant  1 heure après l'injection.
4. En utilisant la partie B, que pouvez-vous dire de la convexité de la courbe CN ? En donner une interprétation concernant le niveau de radioactivité dans le corps de la patiente.
f"(x) = x e-x, donc N"(t) =100 t e-t.
N"(t) est positive sur ]0 ; +oo[.
Donc N'(t) est croissante sur ]0 ; +oo[.
Sur cet intervalle N(t) est décroissante.
Le niveau de radioactivité diminue de moins en moins vite.



  
menu