Mathématiques
: QCM
;
concours Geipi Polytech 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
QCM.
40 points.
Calculs. Exercice 1.
I.A. 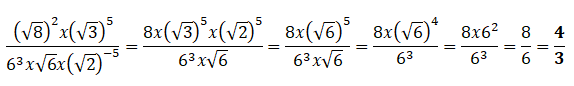 Vrai Vrai
I B.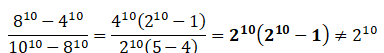 Faux. Faux.
I.C.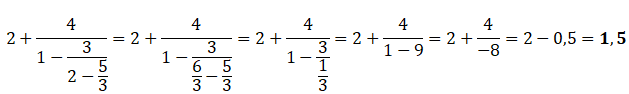 Vrai. Vrai.
I.D. Pour tout entier naturel 𝑛 et tout réel
a non nul :
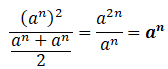 Vrai. Vrai.
I.E. Pour tout réel a supérieur ou égal à 1 :
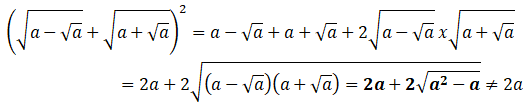 Faux
pour a différent de 1. Faux
pour a différent de 1.
I.F. ln(105)
-ln(103)-ln(0,01) =5 ln(10) -3 ln(10)+2 ln(10) =4 ln(10) = 2
ln(100). Vrai.
Exercice II.
II.A. Soit m un
nombre réel.
L’équation x2 + (m + 1)x + 1 = 0, d’inconnue x, n’admet pas
de solution réelle si et seulement si m appartient à ]−3 ; 1[. Vrai
Discriminant D =
(m+1)2-4=(m+1)2-22= (m+1+2)(m+1-2)=(m+3)(m-1).
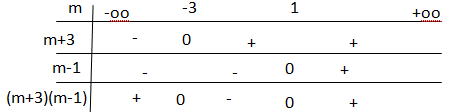
Le discriminant est négatif si m appartient à
]−3 ; 1[. Dans ce cas il n'y a pas de solution réelle.
II.B. Soit m un nombre réel strictement
inférieur à 2.
L’ensemble S des solutions réelles de l’inéquation (x-m) / (m-2)
> 3, d’inconnue x, est S = ]4m − 6 ; +∞[. Faux.
m-2 étant strictement négatif :
(x-m) < 3(m-2) ; x-m < 3m-6 ; x <4m-6.
L’ensemble S des solutions réelles de
l’inéquation (x-m) / (m-2)
> 3, d’inconnue x, est S = ]-oo ; 4m-6[.
Exercice III.
Soient x
et y deux réels non nuls.
III.A. Si 𝑥 < 2𝑦, alors x2 < 2xy. Faux.
Si x est négatif, 𝑥 < 2𝑦, implique x2 > 2xy.
III.B. Si x < 2y, alors 2x < x+2y. Vrai.
Addition du même nombre réel x de chaque côté de l'inégalité.
III.C. Si x < 2y, alors x2
< 4y2.
Faux.
Contre exemple : x = -4 ; y = 1 ; x2 =16 et 4y2 =
4.
Deuxième partie – Fonctions
Exercice IV.
Soient f la
fonction définie sur R par f(x) = (ex-1) / (1+ex)
et C sa courbe représentative dans un repère orthonormé.
IV.A. C admet une
asymptote d’équation y = 1. Vrai.
Si x tend vers +oo, mettre ex en facteur et simplifier :
f(x) = (1-1/ex) / (1+1/ex)
1/ ex tend vers zéro et f(x) tend vers 1.
IV.B. C admet une asymptote
d’équation y = -1. Vrai.
Si x tend
vers -oo, le terme en exponentielle tend vers zéro ;
ex -1 tend vers -1et 1+ex tend vers 1.
IV.C. C admet une asymptote d’équation x= 1. Faux.
f est définie et continue sur R : f(1) = (e-1) / (e+1).
IV.D. f est
décroissante sur R. Faux.
Calcul de la dérivée en posant u = ex-1 et v = 1+ex
: u' = ex ; v' = ex.
(u'v-v'u) / v2 =ex(1+ex -ex+1) /(1+ex)2
= 2ex /(1+ex)2 >0.
f(x) est strictement croissante sur R.
IV.E. Pour tout
réel x, f(-x) = (1-ex) / (1+ex). Vrai.
f(-x) = (e-x-1) / (1+e-x).
Mettre e-x en facteur et simplifier :
f(-x) = (1-1/e-x) (1/e-x+1)=(1-ex) / (1+ex).
|
...
|
....
|
Troisième
partie. Suites numériques.
Exercice V.
Si (un
) avec n entier naturel non nul, est une suite telle que |un
− 1| <
1/ n
pour tout entier naturel 𝑛 non nul, alors :
V-A. Pour tout
entier naturel n non nul, −1 −
1/n < un
<
-1+1/n. Faux.
Contre exemple : soit la suite définie par un = 1.
|un − 1| =0 donc |un − 1| <
1/ n.
1 > -1+1/n, l'encadrement n'est pas vérifié.
V.B. La suite est
majorée par 2. Vrai.
1-1/n < un
< 1+1/n
< 2.
V.C. La suite est
minorée par 0. Vrai.
Pour tout entier naturel n non nul : 0 < 1-1/n < un < 1+1/n.
V.D. La suite
converge vers 0. Faux.
Pour tout entier naturel n non nul : 0 < 1-1/n < un < 1+1/n.
Quand n tend vers +oo : 1+1/n et 1-1/n tendent vers 1.
D'après le théorème des gendarmes, un tend vers 1.
Par unicité de la limite, un ne peut pas converger vers zéro.
Exercice VI.
On dispose des grains de riz sur les 64 cases d’un échiquier : un
sur la première case et on double la quantité
d’une case à l’autre.
VI-A- Le nombre de
grains de riz placés sur la dernière case est 2
63
. Vrai.
Le nombre de grains de riz est une suite géométrique de raison 2 et de
premier terme u0 = 1.
Le 64ème terme de cette suite est : u63 = u0
x 263=263.
VI-B- Le nombre total de
grains de riz placés sur l’échiquier est 2
64 − 1. Vrai.
Somme des 64 premiers termes de cette suite géométrique :
S = 1-264 / (1-2)=2
64 − 1.
Géométrie dans le plan.
Exercice VII.
On considère les vecteurs suivants :
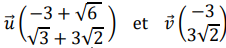
VII.A. 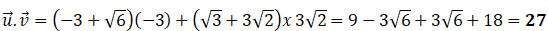 Vrai. Vrai.
VII.B.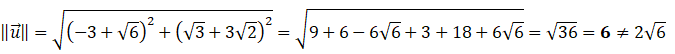 Faux. Faux.
VII-C.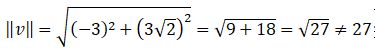 Faux. Faux.
Exercice VIII
Dans le plan rapporté à un repère orthonormé, on considère les points
A, B et C tels que :
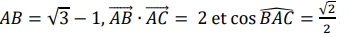
VIII.A.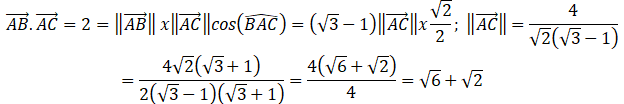 Vrai Vrai
VIII-B. L'angle BAC
mesure 30°. Faux.
cos 30 = 3½ /2 différent de 2½ /2.
|
|
=
|
|