Mathématiques
: limites, géométrie plane, logarithme et exponentielle,
concours TeSciA 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. Calculs de limites.
Dans
cet exercice, on considère les fonctions
f(x) = 3x2 −5x +2 et g(x)=1/x.
M1. Quand x tend
vers +∞, la quantité f (x) tend vers +oo. Répnse A.
M2. Quand x tend
vers −∞, la quantité f (x) tend vers +oo. Répnse
A.
M3. Quand x tend vers +∞, la quantité g(x) tend vers zéro. Répnse
C.
M4. Quand x tend
vers 0 avec x < 0, la quantité g(x) tend vers -oo. Répnse
B.
M5. Quand x tend
vers 0 , la quantité f (g(x)) tend vers :
g(x) tend vers ±oo ; f(g(x)) tend vers +oo. Répnse
A.
M6. Quand x tend
vers 0 , la quantité g( f (x)) tend vers :
f(x) tend vers 2 ; g(
f (x))=g(2)
= 0,5.
Répnse E.
M7. Quand x tend
vers −∞, la quantité g( f (x)) tend vers :
f(x) tend vers +oo ; g(f(x)) tend vers zéro. Répnse
C.
M8. Quand x tend
vers +∞, la quantité f (g(x)) tend vers :
g(x) tend vers zéro ; f(g(x)) = f(0) = 2.
Répnse E.
M9. Quand x tend
vers 1 , la quantité f (x) / (x-1) tend vers :
f(x) = (x-1) (3x-2) ; f(x) / (x-1) = 3x-2.
Quand x tend vers 1, f(1) / (x-1) tend vers 1.
Répnse
C.
M10. Quand x tend
vers 1 , la quantité [f (x)−4] /(x-2) tend vers :
f(x)-4
= 3x2-5x-2 ; f(1)-4 = -4 ; x-2 tend vers -1 ;
[f
(x)−4] /(x-2) tend vers 4.
Répnse E.
L1. Donner la
limite de [f(x)-4] / (2 g(x)-1) lorsque x tend vers 2.
f(x)-4=3x2-5x-2
=(x-2) (3x+1)
; 2g(x) -1 =2 /x -1 = (2-x) / x.
[f(x)-4]
/ (2 g(x)-1)= -x (3x+1) tend vers -14.
Répnse E.
Exercice 2. Géométrie plane.
On considère un triangle ABC rectangle en C tel que l’angle BAC mesure
p / 3.
. On dispose sur le côté [A,B] d’un point D tel que AD = 1 dont le
projeté orthogonal E sur (AC) vérifie EC = 1 et est sur le segment [AC].
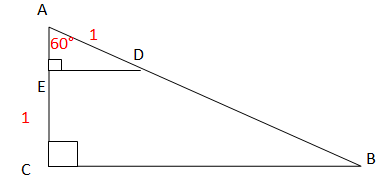
M11. La
distance AE vaut :
AE = AD sin 30 = 0,5.
Répnse D.
M12. La distance DE vaut :
DE = AD cos 30 =3½ /2.
Répnse C.
M13. La mesure de
l’angle ABC est : 30 °.
Répnse B.
M14. La distance DB
vaut :
sin 30 = AC / AB ; AB = AC / 0,5 = 2 AC.
AC = CE+EA =1+0,5 = 1,5 ;
AB = 3 ; DB = AB-AD = 3-1=2.
Répnse D.
M15. La distance BC
vaut :
BC2 = AB2-AC2 =32-1,52=6,75=27
/4 ; BC = 3*3½ / 2.
Répnse E.
M16. La distance DC
vaut :
DC2
= AD2+AC2-2AD * AC cos 60 =1+1,52-3
*0,5 =1,75 = 7 /4 ;
DC = 7½ /2.
Répnse B.
M17. La valeur de
cos(DCE) est :
AD2
= CD2+AC2-2CD * AC cos (DCE) ;
cos
(DCE) = (-AD2
+ CD2+AC2) / (2CD * AC )=(-1+1,75 +2,25) /
(2*1,75 *1,5)=1 / 1,75 =4 / 7.
Répnse E.
M18. Quelle valeur proposée est la
plus proche de sin(DCE) ? Justifier votre réponse.
sin2(DCE)=1-cos2
(DCE)=1-16 /49 =33 / 49 ~36 /49
sin(CDE) ~6 /7 ~0,9.
Répnse E.
M19. Quel
intervalle contient la mesure de l’angle BDC ?
cos(DCE)
~0,57 ; l'angle (DCE) mesure environ 55 °. L'angle (DCB ) mesure
environ 90-55=35°.
L'angle
(DBC) mesure 30 °.
L’angle
BDC mesure environ 180-30-35 ~85°.
Répnse A.
Exercice 3. Logarithme et
exponentielle.
M20. la quantité ln(16) est aussi égale à :
ln(16) = ln(24)=4 ln(2).
Répnse D.
M21. la quantité ln(e½)+ln(1/e) est aussi égale à :
½ln(e) -ln(e) = -½ln(e) = -0,5.
Répnse B.
M22. La quantité suivante est égale à :
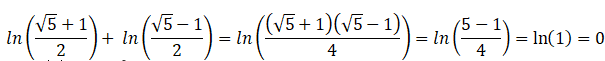
Réponse A.
M23 L’équation x2+4x +3 = x +7 possède :
x2+3x -4 = 0.
Discriminant : 32+4*4=25.
Solutions : (-3+5) /2 =1 et (-3-5)/2 = -4. Réponse C.
M24. L’équation ln(x2 +4x +3) = ln(x +7) possède :
ln(x2 +4x +3) - ln(x +7)=0.
ln[(x2 +4x +3) /(x+7)] =ln(1).
(x2 +4x +3) /(x+7) = 1
x2 +4x +3 = x+7.
x2 +3x -4 =0.
Discriminant : 9+16=25.
Solutions : (-3+5) / 2 = 1 ; (-3-5) / 2 = -4. Réponse C.
M25 L’équation ln(x +1)+ln(x +3) = ln(x +7) possède :
ln((x+1)(x+3)) -ln(x+7) =0= ln(1).
(x+1)(x+3) / (x+7) = 1 ; (x+1)(x+3) = x+7.
x2+4x+3=x+7 ; x2+3x-4=0. Deux solutions. Réponse C
M26. L’équation exp(x2)=1 /9 possède :
x2 = ln(1/9) ; x2 >0 et ln(1/9) < 0. Donc aucune solution. Réponse A
M27 L’équation 3ex −7e−x −20 =0 possède :
On pose X = ex >0.
3 X-7 /X-20 =0 ; 3 X2-20 X-7=0.
Discriminant : 202+4*3*7=316=4 x79 ~182.
On retient les 2 solutions positives : (20±18) / 6. Réponse C.
L2 Donner les solutions de l’équation ex +e1−x −e −1= 0.
ex +e1 / ex −e −1= 0.
On pose X = ex >0 : X+e /X -e-1=0 ; X2-(e+1)X+e=0.
Discriminant : (e+1)2-4e=e2+1+2e-4e =e2-2e+1 =(e-1)2.
Solutions :X= [(e+1) +(e-1) ]/ 2 soit e et X=[(e+1) -(e-1) ]/ 2 =1.
e = ex ; x=1 et 1 = ex soit x = 0.
M28 L’inéquation suivante a pour ensemble de solutions :
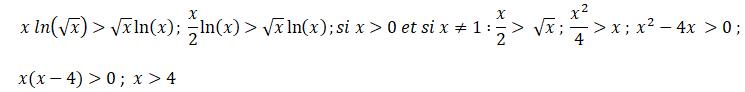
Réponse D.
|
|