Mathématiques
: calcul de dérivées, équations,
concours TesciA 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Calculs de fonctions dérivées.
M29. La fonction f(x) = ln(5x-1) est :
- définie pour 5x-1 >0 soit x > 1 /5.
- calcul de sa dérivée en posant u = 5x-1 ; u' = 5 ; f '(x) = u' / u = 5 /(5x-1).
. Répnse A.
M30. La fonctionf(x) =ln(|7-2x|) est :
- définie pour 7-2x différent de zéro soit x différent de 7 /2.
- calcul de sa dérivée :
Si x < 7 /2, |7-2x| = 7-2x ;
On pose u = 7-2x ; u' = -2 ; f '(x) = u' / u = -2 /(7-2x)=2/ (2x-7).
Si x > 7 /2, |7-2x| = 2x-7 ;
On pose u = 2x-7 ; u' = 2 ; f '(x) = u' / u = 2 /(2x-7).
Répnse B.
M31. La fonction f(x)= ln(ln(x)) est :
- définie pour ln(x) >0 soit x > 1.
-Calcul de la dérivée en posant u = ln(x) ; u' = 1 /x ; f '(x) = u' /u = 1 /(x ln(x)).
Répnse E.
M32. La fonction f(x) = ln( x+(1+x2)½) est :
- définie sur : (1+x2)½> x ;
x+(1+x2)½>0. soit x différent de zéro.
calcul de sa dérivée en posant u = x+(1+x2)½ ; u' = 1+0,5 *2x / (1+x2)½ = 1+x / (1+x2)½ .
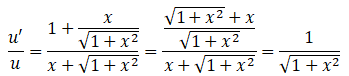
Répnse
B.
Une fonction étonnante.
On considère la fonction f(x) = exp(1 /(x2-1)) sur ]-1 ; 1[.
L3 .Calculer la dérivée f '(x).
On pose u = 1 /(x2-1) =(x2-1)-1 ; u' =-2x / (x2-1)2 .
f '(x) =u' exp(u) = -2x / (x2-1)2 exp(1 /(x2-1)).
M33.Parmi f et sa dérivée f ′, lesquelles tendent vers 0 en 1?
Si x tend vers 1+ : 1 /(x2-1) tend vers +oo et f tend vers +oo.
-2x/ (x2-1)2 tend vers -oo et par produit des limites f ' tend vers -oo.
Si x tend vers 1- : 1 /(x2-1) tend vers -oo et f tend vers 0.
-2x/ (x2-1)2 tend vers -oo et par produit des limites f ' tend vers -oo.
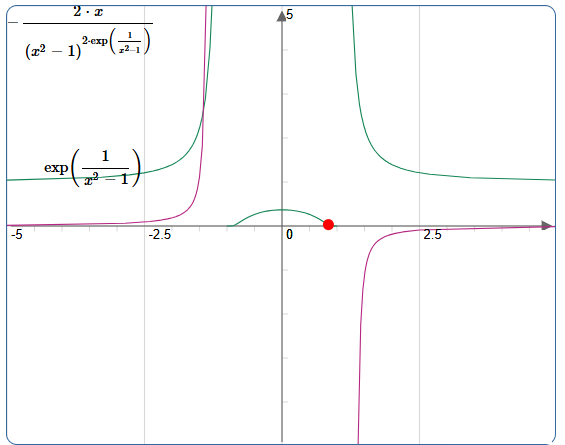
Répnse A.
L'équation ax = xa.
On fixe a dans R∗+
. On se propose d’étudier, selon les valeurs de a, le nombre de solutions de l’équation
(Ea) ax = xa
où l’inconnue x est dans R∗+.
On définit, pour tout a dans R∗+ la fonction ha sur R∗+ par :
ha(x) = x ln(a)−a ln(x).
Étude du cas où a = e.
M34 La fonction ha est :
he(x) = x ln(e) -e ln(x) =x-e ln(x).
Dérivée he'(x) =1-e /x =(x-e) / x.
he'(x) < 0 sur ]0 ; e[ et he(x) est strictement décroissante.
he'(x) > 0 sur ]e ; +oo[ et he(x) est strictement croissante.
Réponse B.
R2. Montrer que x / ln(x) > e pour tout réel x >1.
f(x) = x / ln(x).
Calcul de f '(x) en posant u =x et v = ln(x) ; u' = 1 et v' = 1/x.
f '(x) =( ln(x) -1 ) / ln(x)2.
Si x =e, f '(x) =0; f(x) = e.
Si x > e, f '(x) > 0 et f(x) est croissante de e à +oo.
Si x appartient à ]1 ; e [, f '(x) < 0 et f(x) est décroissante de +oo à e.
Etude du cas où a = 2.
M36. La fontion h2 (x) =x ln(2) -2 ln(x) est :
Calcul de la dérivée : h'2(x) =ln(2)-2 /x =( x ln(2) -2) / x.
h'2(x) = 0 si x = 2 / ln(2).
h'2(x) < 0 si x < 2 / ln(2) ; h2(x) est strictement décroissante.
h'2(x) > 0 si x > 2 / ln(2) ; h2(x) est strictement croissante.
.
Réponse A.
Donner l'ensemble des solutions de (E2).
2x = x2
x ln(2) = 2 ln(x).
ln(x) = ½x ln(2).
exp(ln(x) = exp(x ln(2) / 2)
x = exp(xln(2) /2).
x=2 ; x = 4.
Etude du cas où 0 < a < 1.
M37. La fonction ha est :
ha (x) =x ln(a) -a ln(x)
h'a (x)= ln(a) -a / x.
h'a (x)=0 si x = - a / ln(a).
h'a (x)>0 si x > -a / ln(a) ; h(a) est strictement croissante.
h'a (x)<0 si x < -a / ln(a) ; h(a) est strictement décroissante.
ha (x) présente un minimum :
.
Répnse A.
Donner l'ensemble des solutions de (Ea).
ax = xa
x ln(a) = a ln(x).
ln(x) = x /a ln(a)= ln(a x/a).
exp(ln(x) = exp( ln(a x/a)
x = a x/a.
x=a .
Etude du cas où 1 < a et a diffère de e.
M38. La fonction ha est :
ha(x) = x ln(a)−a ln(x).
h'a (x)= ln(a) -a / x.
h'a (x)=0 si x = a / ln(a).
h'a (x)>0 si x > a / ln(a) ; h(a) est strictement croissante.
h'a (x)<0 si x < -a / ln(a) ; h(a) est strictement décroissante.
ha(x) présente un minimum négatif.
ha(a / ln(a) =a-a ln[a / ln(a)]=a [1-ln[a / ln(a)] < 0
.
Répnse D.
|
|