Evaluation TeSciA, mathématiques générales 2025.
Logarithme et exponentielle.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.. . .

.
.
.. ..
......


...

M20. La quantité ln(16) est aussi égale à :
ln(16) = ln(24)=4 ln(2). Réponse D.

M21. la quantité ln(e½)+ln(1/e) est aussi égale à :
ln(e½)= ½ln(e) = ½.
ln(1/e) = - ln(e) = -1.
 ln(e½)+ln(1/e)= 0,5-1 = -0,5. Réponse B.

M22.  La quantité ln((5½+1) / 2) +ln((5½-1) / 2) est aussi égale à :
ln((5½+1)(5½-1) / 4)=ln((5-1)/4)=ln(1)=0.  Réponse A.

M23. L’équation x 2 +4x +3 = x +7 possède :
x 2 +3x -4 =0.
Discriminant D = 32+4*4=25 =52.
Solutions x1 = (-3+5) / 2 =1 ; x2 = (-3-5) / 2 =-4.
 Réponse C.

M24. L’équation ln(x 2 +4x +3) = ln(x +7) possède :
x+7 >0 soit x > -7.
x 2 +4x +3 >0 .
Résolution de x 2 +4x +3 =0 ; D =42-4*3=4=22 ; solutions x1 =(-4+2) / 2 = -1 et x2 =(-4-2) / 2 =-3.
soit x  < -3 et x > -1
x doit appartenir à ]-7 ; -3[ union ]-1 ; +oo[.
ln(x 2 +4x +3) - ln(x +7)=0.
ln((x 2 +4x +3) / (x+7) )=0 = ln(1).
x2+4x+3 = x+7.
 x 2 +3x -4 =0.
Discriminant D = 32+4*4=25 =52.
Solutions x1 = (-3+5) / 2 =1 ; x2 = (-3-5) / 2 = -4.
Solutions retenues : 1 et -4.  Réponse C.

M25. L’équation ln(x +1)+ln(x +3) = ln(x +7) possède :
x+1 >0 soit x > -1 ; x+3 >0 soit x > -3 ; x+7 > soit x > -7.
ln((x+1)(x+3) )= ln(x+7).
ln((x+1)(x+3) )- ln(x+7).=0
ln((x+1)(x+3) / (x+7)) = 0 = ln(1).
(x+1)(x+3) / (x+7) =1 ; (x+1)(x+3) = x+7.
x2+4x+3=x+7 ; x2+3x-4=0.
Solutions 1 et -4.
Seule la solution -1 est retenue. Réponse B.

M26. L’équation exp( x2) = 1/ 9 possède :
x2 = ln(1/9) = -ln(9).
 x2 >0 ; -ln(9) < 0. Donc aucune solution.
Réponse A.

L2. Donner les solutions de l’équation ex +e 1−x −e−1 = 0.
ex +e1 * e−x −e−1 = 0. Multipions chaque terme par ex :
 e2x +e1 −(e−1) ex= 0.
On pose X = ex >0.
X2-(e-1)X+e=0.
Discriminant D =(e-1)2-4e = e2-6e+1 < 0.
Aucune solution réelle. Réponse A.
M28. L’inéquation x ln(x½) > x½ ln(x) a pour ensemble de solutions :
On pose X = x½ > 0.
X2 ln(X) > X ln(X2) ; X2 ln(X) > 2X ln(X) ; X >2 ;
x > 4. Réponse D.

M29 La fonction f(x) =ln(5x-1) est :
Définie sur : 5x-1 >0 soit x > 1 /5.
On pose u = 5x-1 ; u' = 5.
f '(x) = u' / u = 5 /(5x-1).
 Réponse A.

M30. La fonction f(x) = ln( |7-2x|) est :
Si 7x-2 >0, |7-2x| = 7-2x, soit x < 3,5.
On pose u = 7-2x ; u' = -2.
f '(x) = u' / u = -2 / (7-2x) = 2 / (2x-7).
Si 7x-2 < 0, |7-2x| = 2x-7, soit x > 3,5.
On pose u = 2x-7 ; u' = 2.
f '(x) = u' / u = 2 / (2x-7).
Réponse B.

M31. La fonction f(x)= ln(ln(x)) est :
ln(x) doit être positif : x > 1.
On pose u = ln(x) ; u' = 1 /x.
f '(x) = u' / u = 1 / (x ln(x)). Réponse E.

M32. La fonction f(x)= ln(x + ( 1+ x2)½ ) est :
Définie sur R.
On pose u = x + ( 1+ x2)½ ; u'=1+0,5 *2x / ( 1+ x2)½ =1+x /( 1+ x2)½ .
f 'x) = u' / u = (1+x /( 1+ x2)½ ) / (x + ( 1+ x2)½).

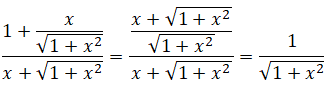
Réponse D.
Une fonction étonnante
On considère la fonction f qui à tout réel x dans ]−1 ; 1[ associe le réel f (x) = exp( 1 / (x2-1)).
 L3 Donner la dérivée de f .
On pose u = 1 / (x2-1) ; u' = -2x / (x2-1)2.
f '(x) = u' exp(u) = -2x / (x2-1)2. exp( 1 / (x2-1))
M33 Parmi f et sa dérivée f ′ , lesquelles tendent vers 0 en 1 ?
Quand x tend vers 1+ : x2-1 tend vers 0+ ; 1/(x2-1) tend vers +oo.
f(x) tend vers +oo.
Quand x tend vers 1- : x2-1 tend vers 0- ; 1/(x2-1) tend vers -oo.
f(x) et f '(x) tendent vers 0.

... =  =
....

 L'équation ax = xa.
Lorsqu’on dispose de réels x et y tels que x > 0, on définit x y = exp(y ln(x)) , ce qui prolonge les définitions connues lorsque y est entier.
On fixe a dans R ∗ + . On se propose d’étudier, selon les valeurs de a, le nombre de solutions de cette équation où l’inconnue x est dans R ∗ + . On définit, pour tout a dans R ∗ + , la fonction ha sur R ∗ + par : ha(x) = x ln(a)− a ln(x).
Étude du cas où a = e .
M34 La fonction ha est :
he(x) = x ln(e)− e ln(x) = x-e ln(x).
Dérivée : he'(x)= 1 -e/ x= (x-e) / x.
he'(x) > 0 sur ]e ; +oo[ ; he(x) strictement croissante.
he'(x) < 0 sur ]0 ; e[ ; he(x) strictement décroissante. Réponse B.
he'(x) = 0 si x = e.
he(x) présente un minimum en x = e. Ce minimum vaut  e-e ln(e) = e-e = 0.

M35 L’équation (Ee) possède une unique solution x=e.
.
R2 Montrer que x / ln(x) > e pour tout réel x > 1.
Etude de f(x) = x / ln(x) :
On pose u = x et v = ln(x) ; u' = 1 ; v' = 1/x.
f '(x) = ( u'v-v' u) / v2 =( ln(x) -1 ) / (ln(x))2.
f '(x) < 0 si 1 < x < e et f(x) est strictement décroissante.
f '(x) > 0 si  x > e et f(x) est strictement croissante.
 f '(x) = 0 pour x = e et f(x) présente un minimum égale à e.

  Étude du cas où a = 2
M36 La fonction h2 est :
h2(x) = x ln(2)− 2 ln(x).
Dérivée : h2'(x)= ln(2) -2/ x.
h2'(x) > 0 sur ]2 / ln(2) ; +oo[ ; h2(x) strictement croissante.
h2'(x) < 0 sur ]0 ; 2/ ln(2)[ ; h2(x) strictement décroissante.
h2'(x) = 0 si x = 2 / ln(2).
h2(x) présente un miniimum en x = 2 / ln(2). Ce miniimum vaut  2-2 ln(2 / ln(2)).
Réponse A.

L4 Donner l’ensemble des solutions de (E2).
h2(x) = x ln(2)− 2 ln(x)=0 si x = 2 et si x = 4.

Étude du cas où 0 < a < 1.
 M37 La fonction ha est :
ha(x) = x ln(a)− a ln(x).
Dérivée : ha'(x)= ln(a) -a/ x.
ha'(x) < 0 ; ha(x) strictement décroissante de +oo à -oo.
Réponse D.

L5 Donner l’ensemble des solutions de (Ea).
x ln(a)− a ln(x).= 0 ; x = a.

Étude du cas où a > 1 et a diffèrent de e.
 M38 La fonction ha est :
ha(x) = x ln(a)− a ln(x).
Dérivée : ha'(x)= ln(a) -a/ x.
ha'(x) > 0 sur ]a / ln(a) ; +oo[ ; ha(x) strictement croissante.
h2'(x) < 0 sur ]0 ; a/ ln(a)[ ; ha(x) strictement décroissante.
ha'(x) = 0 si x = a / ln(a).
h2(x) présente un miniimum en x = a / ln(a)strictement positif.
Réponse C.

M39 L’équation (Ea) a exactement une solution b différente de a, et :
b = a / ln(a) > 0.



  
menu