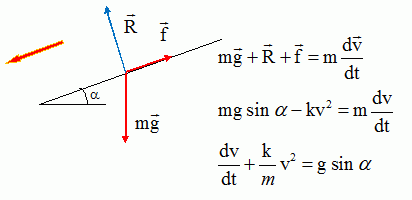|
Mouvement d'un cycliste : Concours officier 1ère classe marine marchande 2009. |
||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
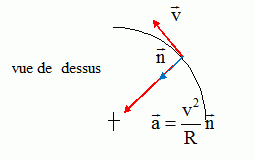
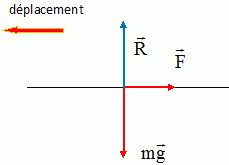
Pour toute cette question, on considère un cycliste et sa bicyclette. La masse totale de l'ensemble vaut m = 80 kg et on prendra pour l'accélération de la pesanteur terrestre g = 9,8 m.s-2. Les conditions initiales sont les suivantes pour les deux parties de cette question : le cycliste s'engage dans une descente rectiligne de longueur L = 300 m assimilée à un plan incliné faisant un angle α = 3° avec l'horizontale, sa vitesse est V0 = 14,4 km.h-1, sa position est repérée par son abscisse x comptée à partir du début de la descente qui s'effectue en roue libre et suivant l'axe de plus grande pente. L'étude porte sur le mouvement du centre de gravité G de l'ensemble cycliste plus bicyclette. On considère que toutes les forces sont appliquées au centre de gravité G. 1ère partie : Les actions résistantes sont négligées. Représenter par un schéma les forces en présence sur le centre de gravité G. Établir l'expression de l'accélération a subie par G. Préciser le nom donné à ce mouvement. Ecrire la seconde loi de Newton suivant un axe parallèle au plan et orienté vers le bas : 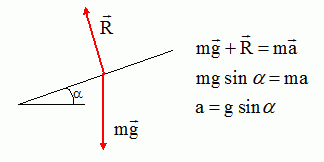 Le mouvement est rectiligne uniformément accéléré. Établir l'expression de la vitesse V de G en fonction du temps. La vitesse est une primitive de l'accélération : v = g sin a t + constante ; la constante est déterminée par la condition initiale v0 = 14,4 /3,6 = 4,0 m/s. v = g sin a t + v0. Établir l'expression de la position x de G en fonction du temps. La position est une primitive de la vitesse : x = ½gsin a t2 + v0t + constante ; la position initiale étant l'origine de l'axe, la constante d'intégration est nulle. x = ½gsin a t2 + v0t. Calculer le temps mis par le cycliste pour arriver en bas de la descente. En bas de la descente x = 300 m ; 300 = 0,5*9,8 *sin 3 t2 + 4,0 t. 300 = 0,2564 t2 + 4,0 t ; t2 +15,6 t -1169,8 ; D = 15,62+4*1169,8 =4922 ; D½ = 70,16 t = 27,28 s ~ 27 s. En déduire la vitesse du cycliste en bas de la descente. Exprimer le résultat en km.h-1. v = 9,8 *sin 3 *27,28 +4,0 = 17,99 ~ 18 m/s. 17,99*3,6 = 64,77 ~ 65 km/h. Le cycliste effectue un virage sur un plan horizontal, sa trajectoire est une portion de cercle de rayon R = 57 m et sa vitesse a pour valeur constante V = 65 km.h-1. Représenter par un schéma la trajectoire et les vecteurs vitesse et accélération.
Calculer l'énergie
cinétique de G juste avant le début du freinage. En déduire la valeur
de l'énergie dissipée par l'action de freinage.
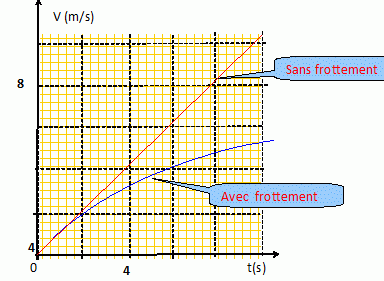
2è partie : Calculer la force constante que doit exercer le cycliste sur terrain plat pour avancer à la vitesse initiale V0 = 14,4 km.h-1. En appliquant un pas de calcul de 2 secondes, calculer la valeur de la vitesse de G à t = 10 s.
Ces valeurs sont donc cohérentes.
|
||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||
|
|