Rebonds, poids apparent, satellite, associations de résistors, solénoïde, loupe : concours kiné Berck 2010

Aurélie 20/04/10

Rebonds, poids apparent, satellite, associations de résistors, solénoïde, loupe : concours kiné Berck 2010.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Rebonds d'une balle .
Une balle est lâchée sans vitesse initiale d'une hauteur h = 2,00 m par rapport au sol. Cette balle élastique effectue une succession de rebonds verticaux. L'énergie cinétique de la balle juste après un rebond diminue de 37 % par rapport à son énergie cinétique juste avant ce rebond. On considère une caméra dont l'objectif est placé dans un plan horizontal situé à une hauteur h'=40,0 cm par rapport au sol. On néglige l'action de l'air sur la balle. Déterminer le nombre de fois où la balle va passer dans le plan de l'objectif de la caméra. (3, 5 ; 7 ; 9 ; 11 ; aucune réponse exacte )
Descente n°1 : la balle passe devant l'objectif et son énergie cinétique avant le rebond n°1 vaut : E_c1=mgh =m *9,81*2,00 = 19,62 m J.
Montée n°1 : énergie cinétique juste après le rebond 1 : (1-0,37)E_c1= 19,62*0,63 m = 12,36 m ( J)
altitude maximale atteinte : 12,36 m = 9,81 m h₁ ; h₁ =1,26 mètre ( second passage devant l'objectif )
Descente n°2 : énergie cinétique juste avant le rebond 2 : E_c2=12,36 m ( 3è passage devant l'objectif)
Montée n°2 : énergie cinétique juste après le rebond 2 : (1-0,37)E_c2= 12,36*0,63 m = 7,787 m ( J)
altitude maximale atteinte : 7,787 m = 9,81 m h₂ ; h₂ =0,794 mètre ( 4è passage devant l'objectif )
Descente n°3 : énergie cinétique juste avant le rebond 3 : E_c3=7,787 m ( 5è passage devant l'objectif)
Montée n°3 : énergie cinétique juste après le rebond 3 : (1-0,37)E_c3= 7,787*0,63 m = 4,91 m ( J)
altitude maximale atteinte : 4,91 m = 9,81 m h₃ ; h₃ =0,500 mètre ( 6è passage devant l'objectif )
Descente n°4 : énergie cinétique juste avant le rebond 4 : E_c4=4,91 m ( 7è passage devant l'objectif)
Montée n°4 : énergie cinétique juste après le rebond 4 : (1-0,37)E_c4= 4,91*0,63 m = 3,1 m ( J)
altitude maximale atteinte : 3,1 m = 9,81 m h₄ ; h₄ =0,36 mètre ( pas de passage devant l'objectif ).
Autre méthode : h=2,00m ; h₁ = 0,63 h = 1,26 ; h₂ = 0,63 h₁ =0,794 ; h _n = 0,63ⁿ h supérieur ou égal à 0,40.
0,63ⁿ *2 supérieur ou égal à 0,40 ; 0,63ⁿ supérieur ou égal à 0,20 ; n inférieur à 3,5.
Il y a donc trois montées avec passage devant l'objectif et 4 descentes.

Poids apparent.
On dispose d'un ressort de masse négligeable, de constante de raideur k = 5,4 N / m et de longueur à vide L₀ = 12 cm. L'extrémité supérieure est fixée à un support horizontal.
On suspend à l'extrémité inférieure de ce ressort une sphère métallique de rayon R = 1,5 cm. La longueur du ressort à l'équilibre est L₁ = 17 cm.
On immerge ensuite complètement la sphère dans un liquide de densité d inconnue. La longueur du ressort à l'équilibre est L₂ = 15 cm.
Calculer la densité du liquide.
( 0,62 ; 0,78 ; 0,85 ; 0,92 ; 0,98 ; aucune réponse exacte )
Equilibre 1 : le poids de la sphère est opposé à la tension du ressort .
mg = k(L₁-L₀) =5,4*0,05 = 0,27 N.
Equilibre 2 : le poids apparent de la sphère est opposé à la tension du ressort .
poids apparent = k(L₂-L₀) =5,4*0,03 = 0,162 N.
Poids apparent = poids - poussée d'Archimède
Poussée = poids - poids apparent = 0,27-0,162 =0,108 N
Poussée = 9,81 * volume de la sphère * masse volumique du liquide.
Volume de la sphère = 4/3 pi R³ =4/3*3,14*(1,5 10^-2)³ =1,413 10^-5 m³ ;
masse volumique du liquide = 0,108 / (9,81 *1,413 10^-5 ) =7,79 10² kg m^-3 = 0,779 g/cm³ ;
La densité a même valeur que la masse volumique exprimée en g/cm³.

Satellite.
Un satelitte de masse m= 530 kg décrit une trajectoire circulaire autour d'une planète de masse M.
Ce satellite se situe à une altitude de h =340 km par rapport à la surface de la planète.
La période de révolution du satellite est T = 1 h 34 min et sa vitesse vaut 7,13 km/s dans le référentiel planètocentrique.
Parmi les affirmations suivantes, relatives à ce satelitte, combien y en a t-il d'exactes ?

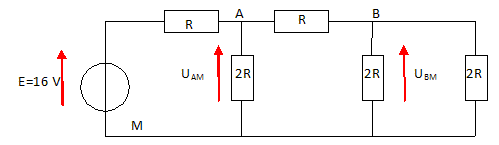
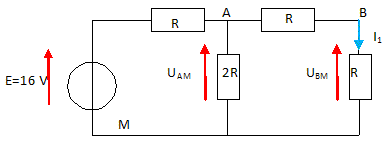
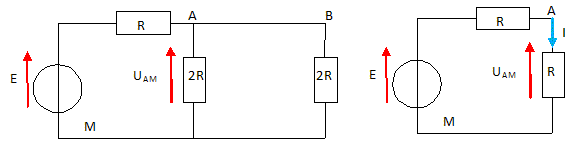
- Le rayon de la planète vaut R = 6,1 10³ km. Vrai.
Le satelitte décrit la circonférence 2 pi ( R+h) à la vitesse v =7,13 10³ m/s en T = 3600+34*60 =5640 s.
2 pi ( R+h) = vT ; R+h = vT/(2 pi) ; R = vT/(2 pi) -h.
R =7,13 10³ *5640 / 6,28 -3,4 10⁵ =6,1 10⁶ m = 6,1 10³ km.
- la masse de la planète vaut M = 4,9 10²⁴ kg. Vrai.
Ecrire la 3è loi de Kepler : T²/(R+h)³ = 4 pi²/ (GM) : M = 4 pi²(R+h)³/ (G T² )
M = 4*3,14²(6,40 10⁶)³ / (6,67 10^-11 *5640²) =4,9 10²⁴ kg.
- la densité moyenne de la planète vaut d = 5,2. Vrai.
Volume de la planète sphérique : V = 4/3*3,14 R³ =4/3*3,14*(6,1 10⁶)³=9,5 10²⁰ m³.
Masse volumique : M/V =4,9 10²⁴ / 9,5 10²⁰ =5,2 kg m^-3 = 5,2 g cm^-3 ; d = 5,2.
- La force gravitationnelle exercée par la planète sur le satelitte a pour valeur F = 4,2 10³ N. Vrai.
F = GMm/(R+h)² =6,67 10^-11 *4,9 10²⁴ *530 / (6,40 10⁶)² =4,2 10³ N.
- Le satellite est soumis à une accélération normale a_N=7,9 m s^-2. Vrai.
a_N = v²/(R+h) =(7,13 10³)² / (6,40 10⁶) =7,9 m s^-2.

Associations de résistors.

Déterminer U_BM en volt. ( 2,0 ; 4,0 ; 6,0 ; 8,0 ; 16,0 ; aucune réponse exacte ).

U_BM = R I₁ ; U_AM = R I₁ + R I₁ = 2U_BM ; U_BM = ½U_AM ;

U_AM = RI ; E = RI+RI = 2 U_AM ; U_AM = ½E ; U_BM = ½U_AM = 0,25 E = 4,0 V.

Solénoïde.
On considère un solénoïde de longueur L = 60 cm dont l'axe est perpendiculaire à la direction de la composante horizontale B_H du champ magnétique terrestre. Une boussole est placée au centre du solénoïde.
Quand on fait circuler un courant d'intensité constante I = 88 mA dans un sens donné, la direction de l'aiguille de la boussole fait un angle aigu a avec l'axe du solénoïde.
En inversant le sens du courant, l'aiguille de la boussole tourne de 151° par rapport à sa position précédente.
Calculer le nombre de spires N de ce solénoïde. ( 420 ; 450 ; 500 ; 520 ; 550 ; aucune réponse exacte ).

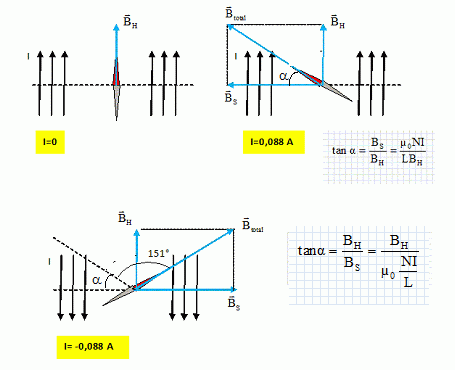
On en déduit a = (180-151)/2 =14,5° et tan a = 0,2586.
N = L B_H / (0,2586µ₀I)= 0,60 *2 10^-5 / (0,2586* 4*3,14 10^-7 *0,088) =420 spires.

La loupe.
Un oeil normal voit tous les objets situés entre l'infini e la distance minimale de vision distincte D_m = 25 cm.
Onutilise une loupe assimilée à une lentille mince convergente de vergence C = 6,0 dioptries.
Un observateur place son oeil " normal " au foyer image de la loupe. Il regarde un objet AB, perpendiculaire à l'axe principal de la loupe, le point A étant situé sur l'axe. On note L la distance algébrisée entre le centre optique et A.
On notera L₁ la valeur que l'on doit donner à L pour que l'image A' de A soit à l'infini.
On notera L₂ la valeur que l'on doit donner à L pour que l'image A' de A soit située à la distance minimale de vision distincte.
La latitude de mise au point de la loupe est L₂-L₁.
Calculer la latitude de mise au point en cm. (11 ; 14 ; 18 ; 20 ; 22 ; aucune réponse exacte )
A' est à l'infini si A est au foyer objet de la loupe : L₁ = -1/C = -1/6,0 =-0,167 m = -16,7 cm.
Appliquer la formule de conjugaison pour calculer L₂.
L'image A'B' se trouve à 25 cm de l'oeil ; l'oeil est à 1/C = 16,7 cm du centre optique O : A' se trouve donc à 25-16,7 =8,33 cm à gauche du cente optique O.

L₂-L₁ = -5,55 -(-16,7) = 11 cm.

menu