|
Le
dihydrogène et son utilisation : concours Mines
2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||||
| .
. |
|||||||
|
|||||||
|
Etude d'une pile à combustible. Les ressources énergétiques ont été largement axées, dans les décennies passées, sur l’utilisation des composés carbonés fossiles (charbon, pétrole, gaz …). L’énergie calorifique ainsi produite étant transformée en énergie mécanique ou électrique. Ce mode de production énergétique présente des inconvénients majeurs : - épuisement des réserves naturelles en combustibles fossiles ; - pollution ; - rendement de conversion faible. La pile à combustible est un mode de production énergétique qui permet de transformer de manière continue de l’énergie chimique en énergie électrique et ce avec des comburants de faible coût. Nous nous intéressons ici à la pile à combustible utilisant le dihydrogène et le dioxygène en tant que comburants, et qui présente donc des avantages écologiques. Considérons une « demi-pile à hydrogène » à la température T = 298 K. 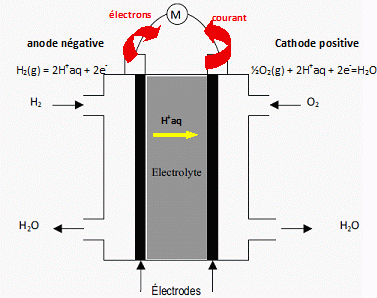 Écrire la demi-équation électronique associée puis l’expression de son potentiel E1 en fonction de la pression en dihydrogène P(H2) et de la concentration en ions oxonium [H+]. H2(g) = 2H+ + 2e- ; E1 = E°( H+/ H2(g)) + 0,03 log ( [H+]2 / P(H2) ). E1 =E1°+ 0,03 log ( [H+]2 / P(H2) ) = 0,03 log ( [H+]2 / P(H2) ). Considérons une « demi-pile à oxygène » à la température T = 298 K. Écrire la demi-équation électronique associée puis l’expression de son potentiel E2 en fonction du potentiel standard E°2, de la pression en dioxygène P(O2) et de la concentration en ions oxonium [H+]. O2(g) +4H++ 4e- = 2 H2O ; E2 = E°( H2O/ O2(g)) + 0,015 log ([H+]4 P(O2) ). E2 = E°2 + 0,015 log ([H+]4 P(O2) = 1,23 +0,015 log ([H+]4 P(O2). La pile globale est formée par l’association de ces deux demi-piles. Écrire l’équation de la transformation globale qui se produit dans cette pile, puis exprimer sa f.e.m. E en fonction de E°2, P(O2) et P(H2). Calculer E pour P(H2) = P(O2) = 1,0 bar.
O2(g) +4H++ 2H2(g) + 4e- = 2 H2O + 4H+ + 4e- ; Synthèse de l'ammoniac. La réaction de synthèse de l’ammoniac s’effectue à partir de dihydrogène et de diazote selon la réaction suivante : 3H2(g) + N2(g) = 2NH3(g). Exprimer l’enthalpie de cette réaction ΔrH°298 en fonction des énergies de liaison E(N≡N), E(N-H) et E(H-H). Calculer ensuite numériquement ΔrH°298. La réaction est-elle endothermique ou exothermique ? E(N≡N) = 940 kJ/mol ; E(N-H)= 380 kJ/mol ; E(H-H) = 430 kJ/mol. 3 liaisons H-H et une liaison triple entre les atomes d'azote sont rompues. 6 liaisons N-H sont reformées. ΔrH°298 = 3E(H-H) + E(N2) -6E(N-H) ; ΔrH°298 = 3*430 +940-6*380 = -50 kJ pour 2 moles d'ammoniac formées : ( -25 kJ / mol ). ΔrH°298 est négative, la réaction est exothermique. Déduire de la question précédente la valeur de l’enthalpie de formation de l’ammoniac ΔfH°(NH3). Justifier la réponse. ΔrH°298 =2 ΔfH°(NH3) -ΔfH°(N2) - 3ΔfH°(H2) ΔfH°(N2) = ΔfH°(H2) = 0 corps purs dans leur état le plus stable ( servant de référence ) à 298 K. ΔfH°(NH3) = 0,5*(-50 )= -25 kJ/mol. Industriellement, la réaction a lieu à 525 °C. Exprimer l’enthalpie de la réaction ΔrH°(T) à cette température en fonction de ΔrH°298 et des capacités thermiques nécessaires. Calculer ensuite numériquement ΔrH°(T). Toutes les capacités calorifiques sont prises égales à 30 J mol-1 K-1 et supposées indépendante de la température. Relation de Kirchhoff : ΔrH°(T) = ΔrH°298 + SDCp DT. ΔrH°(T) = ΔrH°298 +[2Cp(NH3)-Cp(N2)-3Cp(H2)] DT. ΔrH°(T) = -50 103-2*30(525-25) = -50 103-2*30*500 = -80 103 J.( -40 kJ /mol).
Cinétique de décomposition de l'ammoniac. On s'intéresse la cinétique de décomposition de l'ammoniac réalisée à volume constant V et à la température T. NH3(g) = ½N2(g) +1,5 H2(g). On suppose cette réaction d'ordre entier ( n différent de 1) et de constante de vitesse k. Ecrire en fonction de n et de k, l'équation différentielle à laquelle satisfait la fonction c(t) = [NH3](t). Vitesse de disparition de l'ammoniac : v = -d[NH3] /dt = -k [NH3]n. En intégrant cette équation différentielle montrer que : 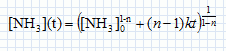 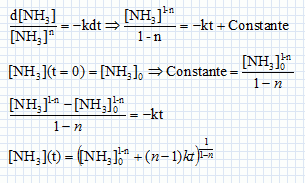 Soit P0 la pression initiale en ammoniac, Exprimer le temps de demi-réaction t½ en fonction de P0, R, T, n et k. Si la réaction est totale, à t½, il reste la moitié de la quantité de matière d'ammoniac initiale, soit : [NH3] (t½) = ½[NH3]0 moles. 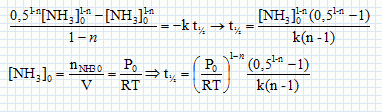 On peut expérimentalement à température fixée T réaliser la mesure des temps de demi-réaction pour différentes valeurs de P0. Comment exploiter cette mesure pour déterminer les valeurs de n et k ? ln t½ = (1-n) ln P0 -ln (RT) + ln((0,51-n-1) / (k(n-1))) Tracer la courbe ln t½ en fonction de ln(P0) ; si la réaction admet un ordre on obtient une droite de pente 1-n et d'ordonnée à l'origine -ln (RT) + ln((0,51-n-1) / (k(n-1))).
|
|||||||
| |
|||||||
|
|