Moteur asynchrone triphasé ( U/f=constante), onduleur, pont redresseur à 4 diodes : bac STI électrotechnique 2011.

. . . .

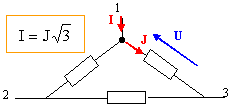
Moteur asynchrone triphasé. Le moteur proposé est un moteur asynchrone aux caractéristiques très atypiques dans la mesure où il est conçu pour fonctionner à basse vitesse. On relève sur sa plaque signalétique les indications suivantes : 27 kW ; 224 tr.min-1 ; 31,5 Hz ; 400 V ; 72,7 A ; cos φ = 0,68. Le couplage triangle est déjà réalisé dans la boîte à bornes. On utilise le réseau triphasé 400V ; 50Hz. Le moteur possède p= 8 paires de pôles.  Déterminer sa vitesse de synchronisme ns lorsqu’il est alimenté à sa fréquence nominale f = 31,5 Hz. ns = f / p =31,5 / 8 =3,9375 ~ 3,9 tr/s.  Quelle est la valeur efficace nominale IN de l’intensité du courant en ligne ? Calculer la valeur efficace nominale JN de l’intensité du courant qui traverse un enroulement.  IN  =72,7 A. couplage triangle : Chaque impédance est alimentée sous une tension composée ; l'intensité du courant dans un fil de ligne I diffère de l'intensité du courant J dans une impédance. JN =IN /3½ =72,7 / 1,73 =41,97  ~42 A.  Calculer pour le fonctionnement nominal : le moment du couple utile TuN ; w =224/60*2 p =23,457 rad/s ; TuN  = Putile /w =27000 / 23,457 =1,15 103 Nm.  la puissance absorbée PaN ; PaN = 3½UI cos φ =1,73*400*72,7*0,68 =34250W ~34,3 kW. le rendement ηN. ηN = Putile / PaN =27 /34,3 =0,787 ~0,79. Etude du moteur alimenté à U/f constant.  Pour fonctionner à basse vitesse, le moteur est alimenté par un variateur qui permet de régler la fréquence en maintenant le rapport U/f constant. Pour la fréquence f = 31,5 Hz, la valeur efficace de la tension entre deux phases du moteur est UM = 400 V. La vitesse vcab de la cabine de l’ascenseur est proportionnelle à la fréquence de rotation n du moteur. Pour une fréquence de rotation n = 225 tr.min-1, la vitesse de la cabine de l’ascenseur est vcab = 2,5 m.s-1. On a représenté la partie utile de la caractéristique mécanique Tu = f(n) du moteur à f = 31,5 Hz. On rappelle que dans un fonctionnement à U/f constant, cette caractéristique se déplace parallèlement à elle-même lorsque la fréquence varie. Le moment du couple résistant noté TR est constant et égal à 1080 N.m. Tracer la caractéristique TR = f(n). Indiquer clairement l’emplacement du point de fonctionnement P pour le moteur alimenté à f = 31,5 Hz couplé à sa charge mécanique. Déterminer la fréquence de rotation n du moteur pour ce point de fonctionnement. 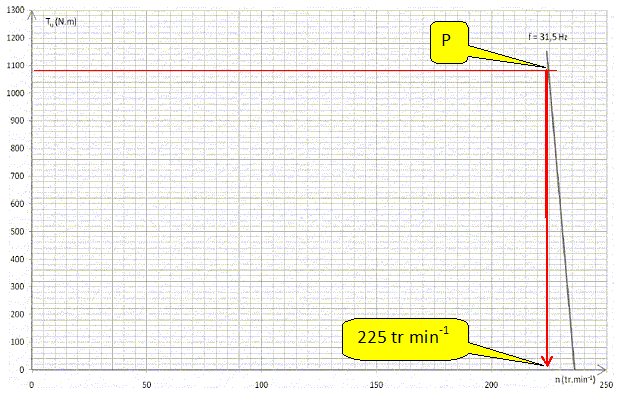En mode maintenance, la fréquence f est réglée à 8 Hz. Tracer sur le document-réponse 2 page 8, la partie utile de la caractéristique mécanique Tu = f(n) du moteur pour une fréquence de 8 Hz. Déterminer la nouvelle fréquence de rotation n’ du moteur et en déduire la vitesse de la cabine. si f = 31,5 Hz : ns = 240 tr/min ; pour f = 8 Hz : ns = 240*8/31,5 = 60 tr/min. 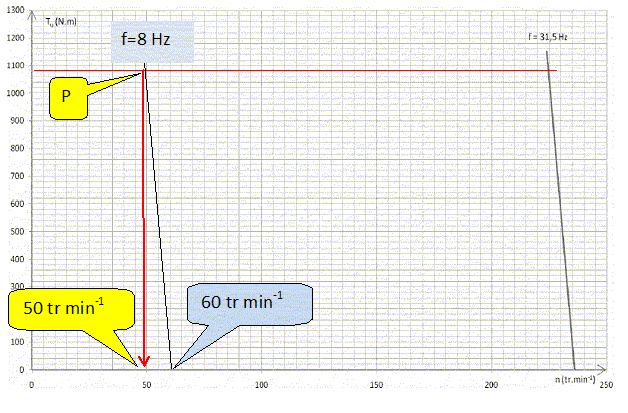La vitesse vcab de la cabine de l’ascenseur est proportionnelle à la fréquence de rotation n du moteur. Pour une fréquence de rotation n = 225 tr.min-1, la vitesse de la cabine de l’ascenseur est vcab = 2,5 m.s-1. vcab = 2,5 *50/225 =0,555 ~0,56 m s-1. Calculer la puissance utile développée par le moteur pour ce point de fonctionnement. Putile = Tu w avec w = 2*3,14 *50/60 =5,236 rad/s et Tu=Tr = 1080 Nm. Putile =1080*5,236 =5,65 kW. Afin d’assurer un positionnement précis de la cabine, le moteur doit être capable de décélérer jusqu’à maintenir la cabine à l’arrêt (et ensuite le frein électromécanique sera serré). Tracer  la partie utile de la caractéristique mécanique Tu = f(n) du moteur permettant de vaincre le couple résistant TR à l’arrêt. 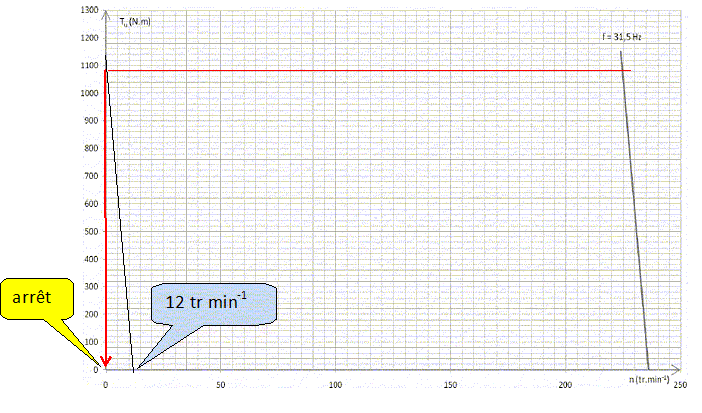Déterminer la fréquence de synchronisme nsa et en déduire la fréquence fa. nsa ~12 tr min-1 = 12/60 =0,2 tr s-1 ; fa = nsa  p = 0,2*8 = 1,6 Hz. Calculer dans ce cas la valeur efficace Ua de la tension entre phases. U / f = constante ; 400 / 31,5 = Ua / 1,6 ; Ua = 400*1,6 / 31,5 =20,3 V. 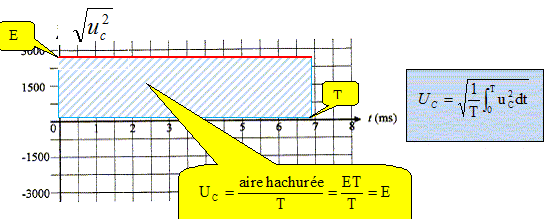Etude de l'onduleur. L’onduleur en question est un onduleur à MLI délivrant un système triphasé de tensions. Cependant, nous nous contenterons ici simplement d’illustrer le principe de l’onduleur. L’étude portera donc sur un onduleur monophasé à commande symétrique alimentant un enroulement du moteur asynchrone. Aucune connaissance spécifique à l’onduleur à quatre interrupteurs n’est nécessaire pour traiter cette partie. 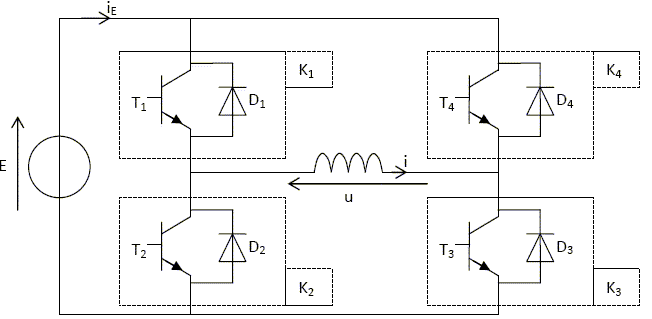L’onduleur est alimenté par une source de tension continue E. On a relevé à l’oscilloscope : - en voie CH1 : la tension u aux bornes de l’enroulement avec une sonde différentielle d’atténuation 1/100 ; - en voie CH2 : l’intensité i du courant traversant l’enroulement avec une sonde de courant de sensibilité 10 mV/A. Pour simplifier l’étude, on a supposé le courant parfaitement sinusoïdal dans la charge. Les blocs K1, K2, K3 et K4 sont des interrupteurs électroniques constitués d’un transistor et d’une diode. Pourquoi peut-on dire qu’ils sont réversibles en courant ? Lorsque le transistor est passant, la diode est bloquée ; lorsque la diode est passante le transistor est bloqué. Chaque interrupteur électronique K est composé d'un transistor et d'une diode D en antiparallèle afin de permettre la conduction dans les deux sens. Préciser, en concordance de temps avec les oscillogrammes, quels sont les interrupteurs (K1, K2, K3, K4) commandés à la fermeture. Sur l'intervalle [0 ;½T ], K1 et K3 sont fermés, K2 et K4 ouverts. Sur l'intervalle [ ½T; T], K2 et K4 sont fermés, K1 et K3 ouverts. Déterminer la fréquence f de la commande de l’onduleur. Période : 6,4 divisions ; 6,4 *5 10-3 = 0,032 s ; f = 1/0,032 =31,25 ~31,5 Hz. Déterminer la valeur crête Û de la tension u. 2 divisions soit 2 *2 =4 V ; tenir compte de l'atténuation 1/100 :  400 V. Calculer, par exemple par la méthode des aires, la valeur efficace Uc de la tension u. Déterminer la valeur crête Î de l’intensité du courant i. 1,2 divisions soit 1,2*0,5 = 0,6 V = 600 mV. Sensibilité 10 mV/A d'où : 60 A. Calculer la valeur efficace I de l’intensité du courant i. I= Imax / 2½ =60/1,414 ~ 42 A.  Quelle est l’expression de la puissance instantanée p reçue par l’enroulement ? En déduire, en concordance de temps avec les oscillogrammes  le signe de cette puissance p et la nature de la phase de fonctionnement. Puissance instantanée = intensité instantanée fois tension instantanée. 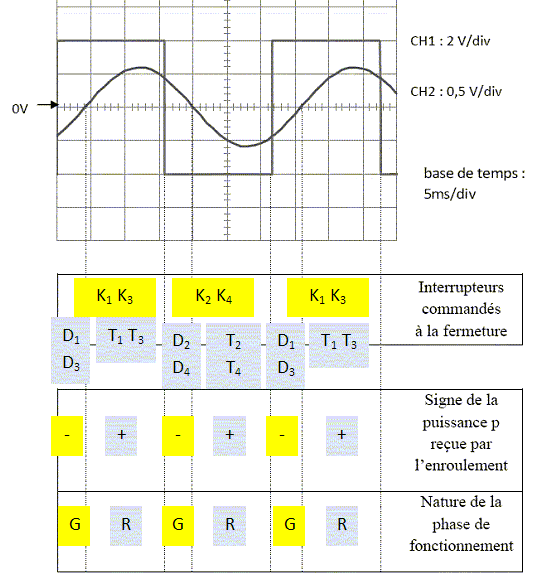G : générateur ; R : récepteur. Etude de l'alimentation du frein. La bobine de commande du frein électromécanique est alimentée par un pont redresseur à 4 diodes. L’entrée du pont de diodes est branchée entre phase et neutre du réseau. La tension v est donc de fréquence 50 Hz et a pour valeur efficace V = 230 V. L’inductance de la bobine du frein est suffisamment importante pour que le courant soit considéré comme parfaitement lissé et constant : ic (t) = <ic (t)> = Ic = 3,35 A. Les diodes sont considérées comme parfaites. Que cela signifie-t-il ? La tension est nulle aux bornes de la diode lorsque celle-ci est passante. Donner l’expression de la tension moyenne <uc> aux bornes de la charge, en fonction de la valeur efficace V. Calculer sa valeur. La tension est nulle aux bornes d'une diode idéale passante : v = uc et <uc> = <v> = V = 230 V. Etablir la relation entre uc, ic et les éléments L et R de la charge. uc = Ldic/dt + Ric. En déduire, sachant que <Ldic/dt > = 0, la relation entre les valeurs moyennes <uc> et <ic>. Calculer la valeur de la résistance R de la charge. <uc> =<Ldic/dt > +<Ric> = <Ric> =R<ic (t)> =R Ic  ; R = V / Ic = 230/3,35 =68,6 ohms. Calculer la puissance dissipée dans la charge. Puissance dissipée par effet Joule RIc2 = 68,6 *3,352 =770 W = 0,77 kW.  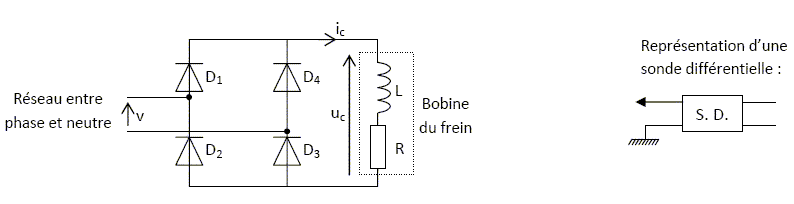Le frein ne se desserre pas. On souhaite visualiser à l’oscilloscope les tensions v et uc pour vérifier le bon fonctionnement du pont redresseur à 4 diodes. Les sondes différentielles utilisées ont un rapport d’atténuation 1/100. Représenter les branchements de l’oscilloscope. 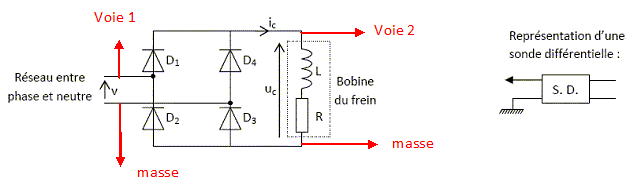Représenter les oscillogrammes attendus, en concordance de temps : 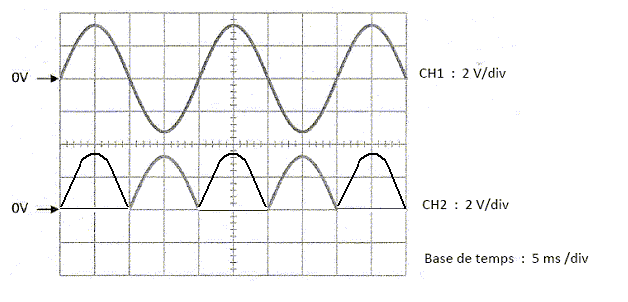Lors de la vérification, on relève les oscillogrammes suivants. Ces oscillogrammes montrent qu’il y a un dysfonctionnement du pont redresseur. 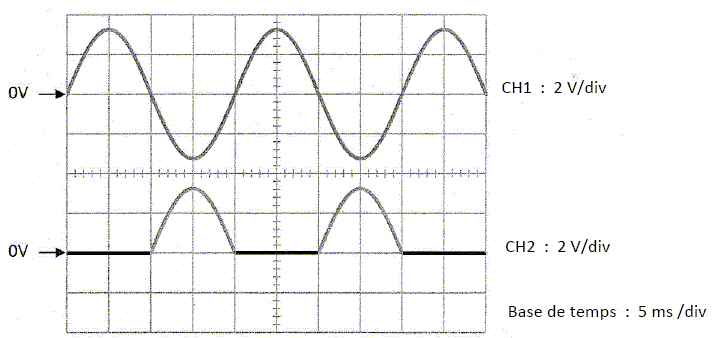 Quelles diodes sont forcément en bon état ? Quelles diodes sont à contrôler ? D1 et D3 ne fonctionnent pas ;  il faut les contrôler. D2 et D4  fonctionnent. Elles sont en bon état.

menu