Etude d'un four de fusion à induction électromagnétique : bac STL chimie de laboratoire 2011.

. . . .

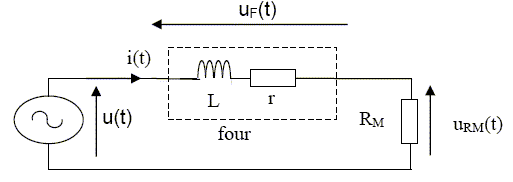
Le chauffage par induction électromagnétique correspond à beaucoup d’applications industrielles et par exemple, pour les bijoutiers, à la fusion de métal comme l’argent. Principe : Une bobine inductrice placée à l’extérieur d’un creuset, qui renferme l’argent à liquéfier, crée de forts courants induits dans l’argent. L’effet joule créé par ces courants chauffe le métal jusqu’à son point de fusion. Schéma de principe. 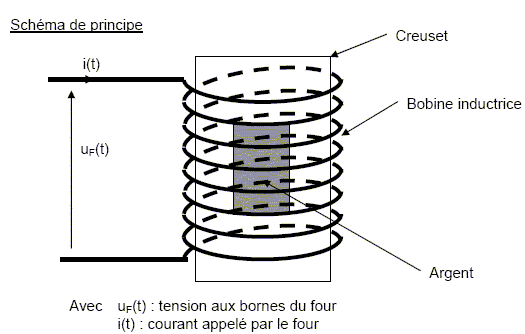Le four à induction, dans les conditions nominales de fonctionnement, est modélisé électriquement par une inductance pure (L) placée en série avec une résistance (r). L’objectif de cette partie est de déterminer de deux manières différentes les caractéristiques électriques (L,r) d’un four à induction de bijoutier. Méthode 1 : Mesure de L et de r à partir de l’observation de tensions électriques. On place en série avec le four à induction une résistance de mesure RM comme indiqué sur le schéma ci-dessous : Avec u(t) : tension d’alimentation sinusoïdale alternative i(t) : courant d’alimentation sinusoïdal alternatif uF(t) : tension aux bornes du four à induction uRM(t) : tension aux bornes de la résistance de mesure RM= 10,0 mW (résistance de mesure). Un oscilloscope permet de visualiser simultanément la tension uRM(t) sur la voie 1 et la tension uF(t) sur la voie 2. On observe alors les oscillogrammes ci-dessous. Déterminer la période et la pulsation de la tension uF(t). Déterminer les valeurs maximales URMmax et UFmax des tensions uRM(t) et uF(t). 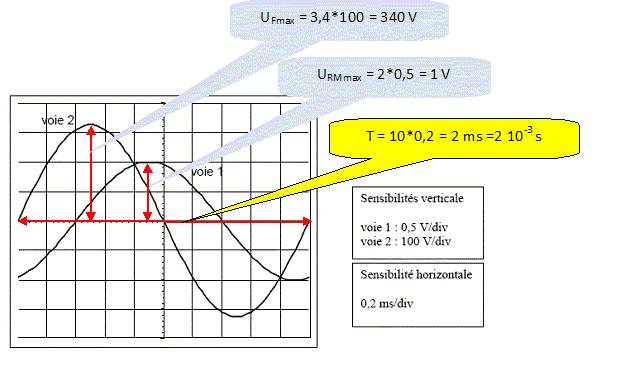Pulsation w = 2p / T = 6,28 / 2 10-3 =3,14 103 rad/s. Déterminer les valeurs efficaces URM et UF des tensions uRM(t) et uF(t). URM = URMmax /1,414 =0,707 ~0,71 V ;  UF = UFmax /1,414 =0,707 ~240 V. En déduire la valeur efficace I du courant i(t). URM = RM I ; I = URM / RM  =0,707 / 0,010 =70,7 ~71 A. Déterminer le déphasage φUF/i de la tension uF(t) par rapport au courant i(t). Justifier le signe. UF(t) est en avance sur URM(t) donc sur i(t). Lorsque les deux fonctions sont croissantes, la première qui passe par un maximum est en avance sur l'autre. 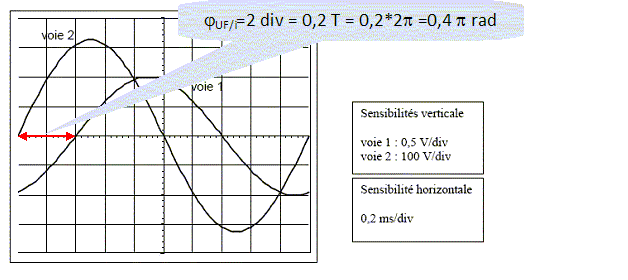 Graphe de Fresnel pour le four à induction : Pour la suite du problème, on prendra UF = 230 V et φUF/i = 1,26 rad. Le four à induction se modélise donc comme ci-dessous : 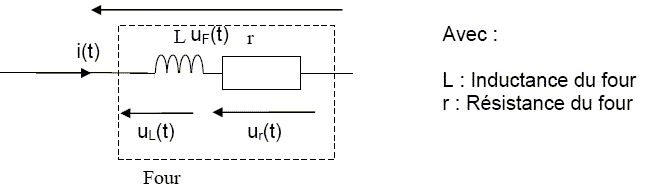Tracer le vecteur de Fresnel UF associé à la tension uF(t) avec i(t) comme référence des phases. (échelle : 1 cm correspond à 20 V ) Rappeler la valeur du déphasage φUL/i de la tension uL(t) par rapport au courant i(t) pour le cas de l’inductance pure L. uL(t) est en avance de ½p par rapport à i(t). De même rappeler la valeur du déphasage φUr/i de la tension ur(t) par rapport au courant i(t) pour le cas d’une résistance r. ur(t) et i(t) sont en phase. En déduire le seul tracé possible pour les vecteurs UL et Ur associés aux tensions uL(t) et ur(t). Effectuer le tracé des vecteurs sur le graphe précédent. Déduire, graphiquement, que la valeur efficace Ur de la tension ur(t) est de 70 V et que la valeur efficace UL de la tension uL(t) est de 220V. 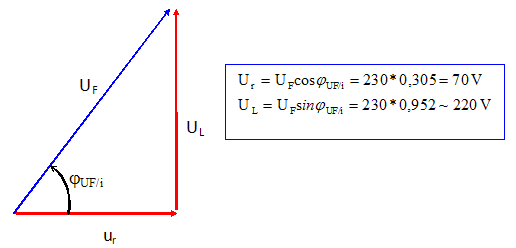Déduire des valeurs précédentes :  La valeur de la résistance r. Ur = r I ; r = Ur/I =70 / 70,7 =0,99 ~1,0 ohm.  La valeur de l’inductance L. UL = Lw I ; L = UL /( Iw ) =220/( 70,7 *3,14 103) =9,9 10-4 ~1 mH. Méthode 2 : Mesure de L et de r à partir d’une mesure de puissance active. Un wattmètre mesure la puissance active consommée par le four : P = 5,00 kW. Une mesure directe du courant efficace appelé par le four donne I = 70,9 A. La tension aux bornes du four a pour valeur efficace UF = 230 V et pour fréquence f= 500 Hz. Le four à induction est toujours modélisé par une inductance pure L en série avec une résistance r.  Quelle est la puissance active PL consommée par l’inductance pure L ? Une inductance pure ne consomme pas de puissance active PL=0. En déduire la puissance active Pr consommée par de résistance r. P =Pr = rI2 = 5,00 kW. Calculer la valeur de la résistance r. r =P / I2 = 5,00 103 / 70,92 = 0,994 ohm. Calculer le facteur de puissance du four. cos f = P / (UFI) =5000 / (230*70,9) =0,3066 ~0,307. ( f =72,14 ° ) Calculer la valeur de l’inductance L du dipôle r,L série qui modélise le four.

menu