Mesure de la viscosité d'une huile moteur : bac STL PLPI 2011.

. . . .

Les conditions d’utilisation d’un moteur de voiture sont étroitement liées au choix de l’huile moteur. Ses propriétés sont fortement dépendantes de la viscosité. Pour déterminer la viscosité η d’une huile moteur S 20W-50 de masse volumique r1, on mesure la vitesse de chute d’une bille sphérique dans un tube vertical rempli de cette huile moteur. L’expérience est réalisée à la température de 22 ° C. On prend les valeurs :  g = 9,81 m. s-2 pour l’accélération de la pesanteur. ρe = 1,0 × 103 kg. m-3 pour la masse volumique de l’eau à 22 ° C. La bille de masse m, de volume V et de rayon R se déplace selon un axe vertical à la vitesse v . Elle est soumise à son poids P = mg , à la poussée d’Archimède F = - r1 V g et à la force de viscosité T exercée par le fluide qui s’oppose au déplacement de la bille et qui est donnée par : T = - 6πηRv. Représenter, sur un schéma, sans considération d’échelle, les forces extérieures appliquées à la bille en chute verticale dans le fluide. 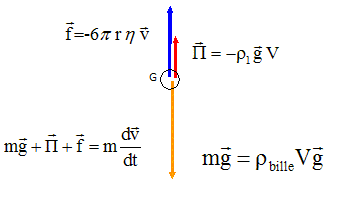Justifier que, au cours de son mouvement, la bille accélère puis que sa vitesse se stabilise à une valeur limite vlim si le tube est suffisamment long. La masse volumique de la bille est supérieure à celle de l'huile et initialement la force de frottement est faible ( vitesse de chute peu importante ). Le poids va donc l'emporter sur les autres forces :la vitesse de chute aumente. Lors de la chute, la vitesse et donc la force de frottement fluide, augmentent : si la durée de la chute est assez longue, les forces vont se compenser et une vitese limite sera atteinte. Décrire un protocole expérimental de votre choix permettant d’observer le mouvement de la bille et de déterminer si elle atteint une vitesse limite. Repérer à intervalle de temps régulier, les positions successives du centre de la bille. Si les distances parcourues pendant des durées égales sont constantes, la vitesse limite est atteinte.   Pour un montage donné, on établit l’existence d’une vitesse limite et on mesure : vlim = 2,60 cm. s-1. On considère le système {bille}. Exprimer la relation fondamentale de la dynamique appliquée au système dans le cas particulier où il effectue un mouvement rectiligne et uniforme. mg = r1gV +6p r h vlim. On mesure la densité de l’huile S 20W-50 avec un densimètre, on trouve 0,884. En déduire sa masse volumique ρ1. r1 =0,884 g cm-3 = 884 kg m-3. La bille a une masse de 1,49 g et un diamètre de 7,15 mm. Vérifier que la masse volumique de cette bille en acier est ρ2 = 7,79 × 103 kg. m-3. V=4/3 pr3= 4/3 *3,14 *(7,15 10-3/2)3 =1,914 10-7 m3. ρ2 =m/V =1,49 10-3 / 1,914 10-7 = 7,79 × 103 kg. m-3.  On trouve pour la viscosité de l’huile l’expression suivante : η = 2r2g(ρ2 -ρ1 ) / (9vlim). On doit introduire dans cette formule un coefficient de correction K qui prend en compte les effets de paroi. K est une constante sans dimension qui ne dépend que des diamètres respectifs de la bille et du tube et ne dépend pas des caractéristiques du fluide ni de la température. Dans ce cadre, on obtient ηcorrigé =  2r2g(ρ2 -ρ1 ) / (9Kvlim).- A l’aide de l’expression de ηcorrigé calculer la viscosité de l’huile moteur si K = 18. ηcorrigé =2*(7,15 10-3/2)2*9,81(7,79-0,884) 103 / (9*18*2,60 10-2) =0,411 Pa s. . 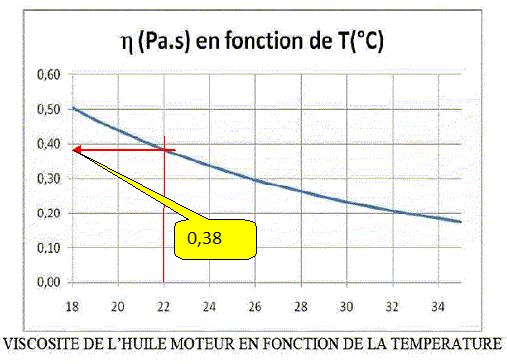Le fabricant donne la variation de la viscosité en fonction de la température (voir graphique ci-dessous). Quel est l’écart relatif entre la valeur de viscosité issue de ce graphe et la mesure précédente ? . (0,411-0,38)/0,38*100 ~8 %.

menu