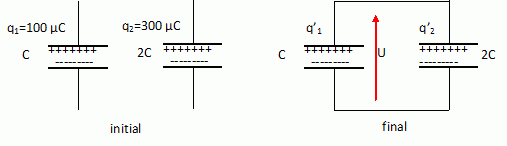QCM  de physique : concours Kiné  2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Le sujet de ce concours n'est pas accessible depuis le site. Célérité des ondes sonores dans un fluide : v2 = µ-1 K-1. µ masse volumique kg m-3 ; K : coefficient de compressibilité Pa-1. L'inverse d'une pression est une surface  divisée par une force et une force est une masse fois une accélération, d'où [K]= m2 N-1 = m2 kg-1  m-1 s2 = m kg-1  s2 ; [µ K] = kg m-3 m kg-1  s2 = m-2 s2  ;  [v2 = µ-1 K-1] = m2 s-2 ; or v est une vitesse [v2] = m2 s-2. v2 = µ-1 K-1est homogène du point de vue des unités. Réponse a. Mesure de la célérité du son dans l'air. Le son émis par le haut parleur est capté par deux microphones M1 et M2 branchés sur les voies YA et YB de l'oscilloscope. On voit deux courbes en phase ; chaque courbe représente deux périodes ; l'écran mesure 10 cm de large ; sensibilité 0,1 ms/cm. Les abscisses x1 et x2 des deux microphones sont repérées sur la règle. Lorsque x1=x2=0 les courbes observées sur l'oscilloscope sont en phase. On laisse le microphone M1 en place et on déplace lentement le microphone M2. On relève l'abscisse x2 de ce microphone à chaque fois que les courbes sur l'oscilloscope sont de nouveau en phase. Les positions correspondantes sont données dans le tableau ci-dessous : position n° 1 2 3 4 abscisse x2 (m) 0,17 0,34 0,51 0,68 Longueur d'onde l = 0,17 m. " chaque courbe représente deux périodes. L'écran mesure 10 cm de large ; sensibilité 0,1 ms/cm" : 2T = 10*0,1 = 1 ms = 10-3 s. T = 5 10-4 s. v = l / T =0,17 /  5 10-4  = 3,4 102 m/s. Réponse b. Lentille convergente.  Réponse d. On donne C 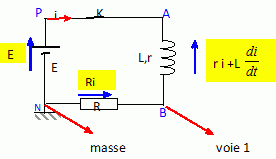= 2,0 µ F. Conservation de la charge : q1+q2 = q'1+q'2 = 400 µC. U = q'1 / C = q'2/(2C) d'où q'1 = q'2 / 2. Par suite q'1+2q'1= 400 µC ; q'1=133 µC et U = 133 / 2 ~67 V. Réponse d.     On donne E = 1200 V ; L = 2,5 H ; r+R = 200 ohms. En régime permanent, l'intensité est constante : di/dt = 0 d'où E= (R+r) I soit I =1200/200 = 6,0 A. La puissance  fournie au circuit est égale à EI = 1200*6 =7200 = 7,2 kW. Réponse d. Fréquence propre du dipole LC. On donne L = 10 mH = 0,01 H et C = 40 nF = 4 10-8 F f = 1 / (2p(LC)½) =1/(6,28 *2 10-5) ~8000 Hz ~ 8,0 kHz. Réponse c. Faire chauffer m = 1,5 kg d'eau de 20°C à 80 °C. On donne la capacité thermique massique de l'eau : c = 4,0 103 J K-1 kg-1. Puissance électrique du chauffage : P = 1,0 kW ; rendement 60%.                 Enegie gagnée par l'eau froide : mc Dq =1,5*4000*60 =3,6 105 J Energie utile du chauffage 0,6 P Dt =600 Dt avec Dt : durée du chauffage. La durée du chauffage est : 3,6 105 / 600 =600 s = 10 minutes. Réponse c. Course de véhicules. 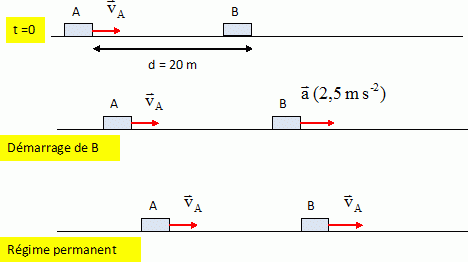Distance parcourue par A : xA = vAt. Distance parcourue par B si la phase de démarrage dure Dt seconde : xB = ½aDt2 +vA(t-Dt) +d. A l'instant où A rattrappe B : xA = xB ; vAt = ½aDt2 +vAt +d ; 0 = ½aDt2 -vA Dt +d. B atteint la vitesse vA au bout d'une durée Dt = vA/a. Par suite : 0 = ½a(vA/a)2 -vA vA/a +d ; ½v2A / a = d ; v2A = 2ad = 2*2,5*20 =100 ; vA = 10 m/s. Réponse d. 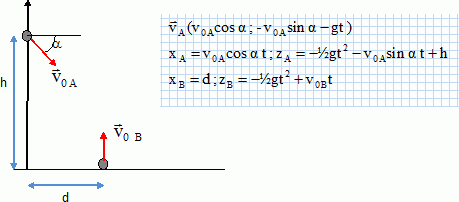A l'instant de la rencontre : xA = xB ; v0 A cos a t = d ; zA = zB ; -v0 A sin a t +h = v0 B t. On donne : v0 A = 10 m/s ; v0 B = 4,0 m/s ; sin a =0,6 ; cos a = 0,8 ; d = 2,0 m. d'où 8 t = 2,0 ; t = 0,25 s et -6*0,25 + h = 4*0,25 ; h = 2,5 m. Réponse a. Chute d'une goutte dans l'air. 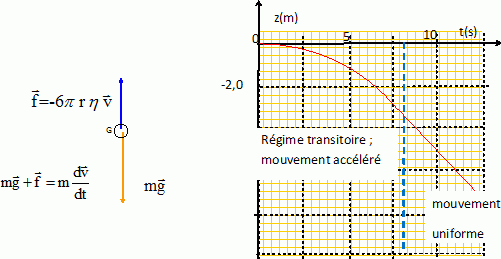La viscosité s'exprime h en Pa s. Quand la vitesse limite vlim est atteinte : mg = 6p rh vlim ; vlim  = mg / (6p r h). Or m = r V; r masse volumique  et V =4/3 pr3 volume d'une goutte sphérique. Vitesse limite = coefficient directeur de la droite  lors du mouvement uniforme soit environ 1 m/s. Réponse a et e. Ballon gonflé à l'helium. 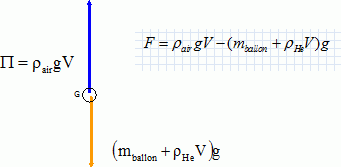On donne : m = 2,0 kg ; rair = 1,2 kg m-3 ; rHe = 0,17 kg m-3 ; V = 7 m3. F = 10 ( 1,2*7 -2-0,17*7) ~ 52 N. Réponse d. Période de révolution T d'un satellite. ( Référentiel géocentrique ). 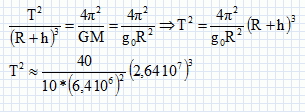La période de révolution est voisine de 12 h. Réponse e. Fréquence et longueur d'un pendule simple. Le pendule n°1 a une longueur L1, une période T1 et une fréquence f1. Le pendule n°2 a une longueur L2, une période T2 >T1 et une fréquence f2 < f1. 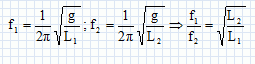Si f1 = 3f2 alors L2 = 9 L1. Réponse d. Oscillateur élastique amorti. Les forces de frottements sont considérées comme étant constantes de valeur f. Ecrire la seconde loi de Newton sur un axe horizontal ; l'origine est la position d'équilibre. Solution particulière de l'équation différentielle : x = f / k. Solution générale de l'équation différentielle sans second membre : x= A cos (wt) avec w2 = k/m et A une constante. Solution générale de l'équation différentielle : x= A cos (wt) + f / k. Or x(0) = x0 d'où : x0 = A+ f / k soit A = x0 - f / k. x(t) = (x0 -f / k)cos (wt) + f/ k. Lors du premier arrêt avant de rebrousser chemin t = ½ T ( période) et : x(½T) = (x0 -f / k) cos 180 + f / k = -(x0 -f / k)+ f / k = -x0 +2f / k. Réponse b. Oscillateur élastique non amorti. Les conditions initiales sont : x(0) = + 2 cm et v0 = 0,2 m/s. On donne w0 = 10 rad/s. x(t) = A cos (w0t+f) ; x'(t) = -Aw0 sin (w0t+f) x(0) =0,02 = A cos f ; x'(0) = -0,2 =-Aw0 sin f ; tan f =1 et f =+45°. Par suite A = 0,02 / cos 45 = 0,028 m x(t) = 0,028 cos (w0t+0,25 p). Réponse b. Energie utile pour allonger un ressort de 2 cm à 3 cm . On donne k =50 N/m. Energie stockée par le ressort si x = 0,02 m : E1 = ½kx2 =25*0,022 =0,010 J = 10 mJ. Energie stockée par le ressort si x = 0,03 m : E2 = ½kx2 =25*0,032 =0,0225 J = 22,5 mJ. E2 -E1 = 12,5 mJ. Réponse e. Oscillations forcées. On not f0 la fréquence propre du résonateur et f la fréquence variable de l'excitateur. Le résonateur ( le solide ) vibre à la fréquence f de l'excitateur ( le vibreur ). Le vibreur impose sa fréquence au solide  fixé au ressort. L'amplitude des oscillations du solide ( le résonateur)  passe par un maximum lorsque f = f0. Réponses c et e.

menu