Spectroscospie à prisme : concours Geipi 2011. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

La spectrométrie est une technique de mesure des longueurs d’ondes correspondant aux raies émises par une source lumineuse. Comme chaque atome (ou chaque molécule) est caractérisé par un ensemble de raies d’émission occupant des positions bien précises dans le spectre, on peut donc déterminer la composition chimique d’une source à partir de l’analyse de la lumière qu’elle émet : ceci est réalisé couramment en astrophysique pour connaître les éléments qui constituent certaines étoiles. On envoie sur un prisme un faisceau lumineux. Le rayon traverse le prisme, puis y sort en étant dévié vers sa base. En mesurant à l’aide d’un goniomètre le minimum de déviation, on peut ainsi déterminer l’indice n du verre crown constituant ce prisme. On notera c = 3 . 108 m.s-1 la célérité de la lumière dans le vide. 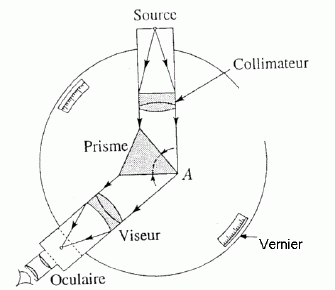La propriété fondamentale à l’origine de la spectroscopie à prisme est que son indice de réfraction dépend de la longueur d’onde. Comment qualifie-t-on un tel milieu ? L'indice de réfraction est lié à la célérité de la lumière dans le prisme. Un milieu est dispersif si la célérité de l'onde dépend de sa fréquence. La dépendance de l’indice du prisme vis-à-vis de la longueur d’onde est correctement décrite par la loi empirique de Cauchy : n(l) = A+B / l2. Sans indication particulière, les longueurs d’ondes données sont considérées mesurées dans le vide ou l’air. On utilise une lumière bleue de longueur d’onde λ1 = 486,1 nm. On mesure n1 = 1,522. Puis, on utilise une lumière rouge de longueur d’onde λ2= 656,3 nm. On trouve n2 = 1,514. Quelle est la fréquence f1 de la lumière bleue avant son passage dans le prisme ? Quelle est sa fréquence f1′ dans le prisme ? La fréquence caractérise une onde, elle est indépendante du milieu de propagation : f1 = f '1. f1 = c / l1 = 3 . 108 / 486,1 10-9 =6,17 1014 Hz ~ 6 1014 Hz. Calculer sa longueur d’onde λ1′dans le prisme. l'1 = l1 / n1 = 486,1 / 1,522 =319 nm. Calculer les valeurs de A et B (B en nm2). 1,522 = A+B / (486,1 10-9)2 = A+4,2320 1012B. (1) 1,514 = A+B / (656,3 10-9)2 = A+2,3216 1012B. (2) (1)-(2) donne : 8,00 10-3 =1,91 1012 B ; B = 4,1885 10-15 m2 = 4188 nm2. (1) donne  : A = 1,522 -4,2320 1012* 4,1885 10-15 = 1,504. On souhaite maintenant déterminer la longueur d’onde d’un laser Argon. Quelle est la nature de l’onde associée au laser ? La lumière, monochromatique, émise par le laser fait partie des ondes électromagnétiques. Pour plus de précision, on remplace le prisme précédant par un nouveau en verre flint, caractérisé par n(l) =A'+B'/ l2 avec A′ = 1,666 et B′ = 12 040 nm². On mesure alors pour ce laser un indice optique n3 = 1,712. Pourquoi les mesures avec ce nouveau prisme seront-elles d’une meilleure précision qu’avec le prisme en verre crown ? B' étant supérieur à B, le verre flint est plus dispersif que le verre crown. Le spectroscope à prisme sera plus sensible aux variations de longueurs d'onde. En déduire la longueur d’onde λ3 de ce laser. n3 = A'+B' / l32. l32= B' / (n3 - A') ; l3= (B' / (n3 - A'))½ ; 1,712 = 1,666 + 12040 / l32. l32= 12040 / ( 1,712-1,666) = 2,617 105 ; l3 = 511 nm.  Quelle est sa couleur ? Il s'agit d'une lumière verte.

menu