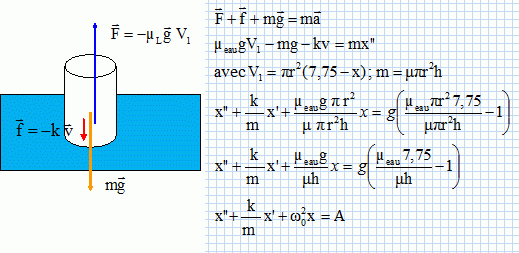L'uranium 235.
L'uranium 235 23592U bombardé par un neutron 10n peut se scinder en deux noyaux plus petits : un noyau de xénon 14054Xe et un noyau de strontium 9438Sr. Cette réaction de fission libère x neutrons.
Il peut aussi bombardé par un neutron 10n peut se scinder en deux noyaux plus petits : un noyau de brome 8535Br et un noyau de lanthane 14857La. Cette réaction de fission libère y neutrons.
AZX
|
42He
|
10n
|
14857La
|
8535Br
|
14054Xe
|
9438Sr
|
23592U
|
masse
en u
|
4,0015
|
1,0086
|
147,932
|
84,916
|
139,9252
|
93,9154
|
235,044
|
1 u = 1,66054 10-27 kg ; c = 3,00 108 m/s.
Ecrire les réactions et donner les valeurs de x et y.
23592U +10n --->14054Xe + 9438Sr + 2 10n.
Conservation du nombre de nucléons : 235+1 = 140 +94 +x ; x = 2.
23592U +10n ---> 8535Br + 14857La + 3 10n.
Conservation du nombre de nucléons : 235+1 = 85 +148 +y ; y = 32.
Calculer en joule l'énergie libérée par la fission d'un noyau d'uranium suivant chacune des réactions.
Dm =m(14054Xe) + m(9438Sr)+ m(10n) -m(23592U) =139,9252+93,9154+1,0086-235,044 = -0,1948 u
-0,1948 *1,66054 10-27 = -3,23473 10-28 kg
E = |Dm|c2 =3,23473 10-28 *9 1016 =2,91 10-11 J.
Dm =m(8535Br) + m(14857La)+ 2m(10n) -m(23592U) =84,916+147,932+2*1,0086-235,044 = -0,1788 u
-0,1788 *1,66054 10-27 = -2,96905 10-28 kg
E = |Dm|c2 =2.96905 10-28 *9 1016 =2,67 10-11 J.
En
déduire l'énergie libérée par la fission d'un kilogramme d'uranium,
sachant que la probabilité de chacune des réactios est la même.
Energie moyenne : ½(2,67 +2,91) 10-11 = 2,79 10-11 J.
Nombre de noyaux d'uranium 235 dans 1 kg : 1000 / 235 *6,02 1023 =2,56 1024.
Puis : 2,79 10-11 * 2,56 1024 =7,1 1013 J.
La réaction si elle n'est pas contrôlée, peut être explosive. Expliquer.
Chaque
fission produit 2 ou 3 neutrons qui peuvent à leur tour réagir avec 2
ou 3 noyaux d'uranium. Il en résulte une réaction en chaine.
Les
noyaux d'uranium 235, présents dans le réacteur, peuvent capter un
neutron rapide pour donner un noyau B. B subit deux désintégrations
naturelles ß- pour donner un noyau de plutonium fissible C.
Identifier et nommer B.
23592U +10n --->23692U. B est un isotope de l'uranium 235. B est l'uranium 236.
23692U ---> 23693D + 0-1e.
23693C ---> 23694Pu + 0-1e.
Le réacteur est appelé surrégénérateur. Justifier.
La fission du combustible uranium 235 conduit à un autre combustible fissible le plutonium 236.
|
Le noyau C possède une radioactivité alpha caractérisée par un temps de demi-vie égal à 24 400 ans.
Ecrire la réaction de désintégration de C et préciser le temps au bout duquel la radioactivité de C a été divisée par huit .
23694Pu ---> 23292U + 42He. A chaque demi-vie l'activité initiale est divisée par deux.
Au bout de 3 demi-vies soit 3*24400 = 73200 ans l'activité initiale est divisée par huit.
|
L'oeil et la vision.
L'oeil
sera représenté par un diaphragme de diamètre D ( pupille) placé
devant une lentille ( cristallin ) de distance focale f'. Les
muscles oculaires modifiant légèrement la forme du cristallin
permettent de réduire la distance focale f'0 ( distance focale sans
effort d'accomodation ) à f'min ( distance focale minimale
obtenue avec un effort d'accomodation maximal ). Le pouvoir
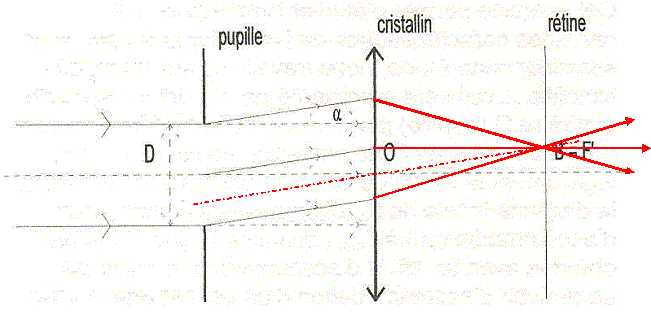
d'accommodation d'un oeil est égal à 1/f'0 -1/f'min. Le récepteur ( rétine ) d'épaisseur e, est constitué de cellules réceptives ( cônes ) de dimension g.
On donne : D = 2 mm ; OB = 2 cm ; e = 80 µm ; g = 10 µm.
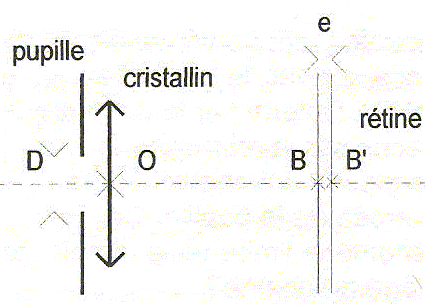
Influence de l'épaisseur de la rétine.
Pour un oeil emmétrope, l'image d'un point situé à l'infini se forme, sans accommodation, dans l'épaisseur de la rétine.
Montrer que cet oeil possède une valeur f'0 comprise entre deux valeurs à calculer très précisément.
L'objet étant à l'infini, la formule de conjugaison indique que la distance focale est égale à la distance cristallin-rétine.
f'01 = OB = 2,000 cm ; f'02 = OB' = OB + e = 2,008 cm ;
f'0 est comprise entre 2,000 cm et 2,008 cm.
La pseudo accommodation liée à l'épaisseur de la rétine est égale à 0,2 dioptrie.
Justifier ce chiffre.
1/ f'012 - 1/ f'0 2 = 1/0,02 -1/ 0,02008 = 50 -49,8 = 0,2 dioptrie.
Influence du diamètre de la pupille et de la dimension des cellules réceptrices.
Pour
cet oeil emmétrope, l'image d'un point situé sur l'axe optique de
l'oeil en A, sans accommodation, se forme en A'. La pupille a un
diamètre D.
Effectuuer le schéma représentant les rayons issus de A et passant aux bords extérieurs de la pupille.
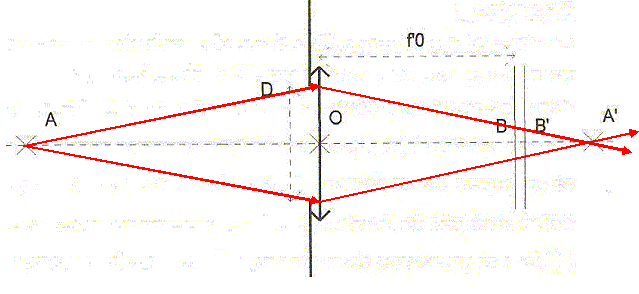
Donner la dimension de la tache que forment les rayons lumineux sur la rétine en fonction de OA', f'0 et D.
On confond ici B et B' ; on prend OB = f'0. On donne d, la dimension de la tache sur la rétine.
D / d = OA' / A'B ; d = D A'B / OA' ; A'B = OA'-OB =OA' -f'0.
d = D (OA' -f'0) / OA'.
L'image sera nette si la dimension de la tache est inférieure à la dimension des cellules réceptives de la rétine.
Exprimer puis calculer OA'max pour obtenir une image nette.
d < g ; D (OA' -f'0) / OA' < g ; D (OA' -f'0) < g OA' ; OA' ( D-g) < D f'0 ;
OA' < D f'0 / ( D-g) ; OA'max = D f'0 / ( D-g) =2 10-3 * 0,02 / (2 10-3 - 10-5) =0,0201 m.
En déduire la position limite de l'objet OAlim ( punctum proximum ) permettant une vision nette.
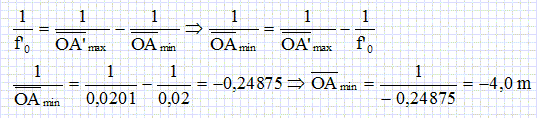
Une
personne de plus de 65 ans a perdu tout pouvoir d'accommodation lié au
muscle oculaire. Il conserve donc les seules pseudo accommodation liée
à l'épaisseur de la rétine et à la dimension des cônes.
En adaptant le calcul précédent pour tenir compte de l'épaisseur de la rétine, déterminer OA'max puis la position de l'objet OAlim permettant une vision nette pour un oeil caractérisé par OB = f'0.
Remplacer OB par OB' = OB + e = 2,008 cm ; soit f'0 = OB' = 2,008 cm.
OA'max = D f'0 / ( D-g) =2 10-3 * 0,02008 / (2 10-3 - 10-5) =0,02018 m.
Distance algébrique OAlim = -2,2 m.
La
pupille de diamètre D est éclairée par un faisceau lumineux parallèle.
A la sortie de la pupille le faisceau forme un cône divergent d'angle 2q.
Citer le phénomène concerné.
Diffraction par une fente dont la dimension est du même ordre de grandeur que la longueur d'onde de la lumière.
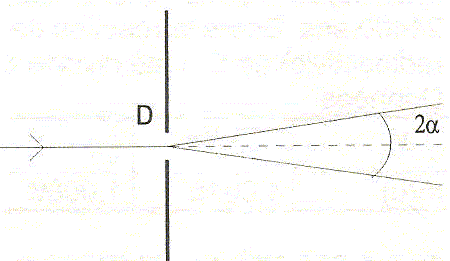
Rappeler l'expression de l'élargissement angulaire 2a d'un faisceau de longueur d'onde l éclairant une fente de largeur D.
a = l / D ou 2a = 2l/D.
Pour quelle couleur cet élargisement est-il le plus important ? Calculer cet élargissement.
La
longueur d'onde du rouge ( 800 nm) est supérieure à celle du
bleu ( 400 nm). L'élargissement est plus important pour le rouge.
a = 800 10-9 / 2 10-3 = 4 10-4 rad ; 2 a = 8 10-4 rad
Tracer le point de convergence des rayons sortant de la pupille avec un angle a.
Déterminer le diamètre d de la tache sur la rétine. Ce phénomène limite-t-il la netteté de l'image rétinienne ?
tan a = ½d / f'0 ; d = 2 f'0 tan a =2*0,02 tan 4 10-4 =1,6 10-5 m = 16 µm pour la lumière rouge.
d = 2 f'0 tan a =2*0,02 tan 2 10-4 =0,8 10-5 m = 8 µm pour la lumière bleue.
Pour
le rouge, le diamètre de la tache due à la diffraction est supérieure à
la dimension d'un cône : la netteté de l'image sera un peu altérée.
|
Vision de nuit :
Lors
de la vision nocturne une caractéristique de l'oeil est modifier pour
augmenter la puissance lumineuse pénétrant dans l'oeil.
Laquelle ? Comment sont modifiés les résultats précédents pour la vision nocturne ?
Le diamètre D de la pupille est bien supérieure à 2 mm. On prend, par exemple D = 5 mm.
OA'max = D f'0 / ( D-g) =5 10-3 * 0,02 / (5 10-3 - 10-5) =0,02004 m. OA'max diminue.
La distance algébrique OAlim = -10 m ; elle augmente.
a = 800 10-9 / 5 10-3 = 1,6 10-4 rad ; 2 a = 3,2 10-4 rad ; a diminue.
d = 2 f'0 tan a =2*0,02 tan 1,6 10-4 =6,4 10-6 m = 6,4 µm pour la lumière rouge.
Pour
le rouge, le diamètre de la tache due à la diffraction est inférieure à
la dimension d'un cône :l'image sera nette.
|
|
Donner la
composition du noyau de radon 222.
Z = 86 ; 86 protons et 222-86 = 136 neutrons.
Le radon 222 est issu du noyau de radium 226
Ecrire l'équation de
cette désintégration. De quel type de radioactivité s'agit-il ?
22688Ra ---> 22286Rn
+ 42He, radioactivité de type alpha.
Donner les deux
autres types de radioactivité en précisant le nom de la particule émise.
Radioactivité de type ß- : émission
d'un électron.
Radioactivité de type ß+ : émission
d'un positon.
Ecrire l'équation de
désintégration du radon 222.
22286Rn
---> 21884Po+ 42He.
Au cours de la désintégration du radon 222, on observe l'émission d'un
rayonnement g.
Définir
cette émission. Quel noyau émet ce rayonnement ?
Le rayonnement g est un
photon, de même nature que la lumière, mais beaucoup plus énergétique.
Le noyau fils 21884Po, se trouve souvent dans un
état excité : lors du retour à l'état fondamental, il libère son
surplus d'énergie sous forme de photon g.
|
On considère un échantillon
contenant à la date t=0, N0 = 1000 noyaux de radon 222.
Calculer
la constante radioactive du radon.
l = ln2 / t½
avec t½ = 3,8 *24*3600 =3,2832 105 s.
l = ln2 / t½ = ln 2 / 3,2832 105= 2,1112 10-6 ~2,1 10-6 s-1.
Ecrire
la loi de décroissance radioactive de l'échantillon. Tracer la courbe
N=f(t) en faisant apparaître la demi-vie.
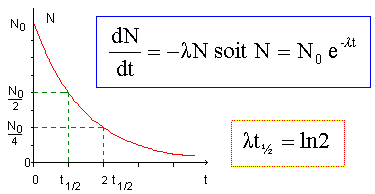
|
A quelle date t1,
il ne reste plus que 1% du nombre initial de noyaux ?
N = 0,01 N0 = N0 exp(-lt1) avec l = ln2 / 3,8 = 0,1824 jour-1.
ln 0,01 = -0,1824 t1
; t1 = 25,2 ~ 25
jours.
Définir l'unité le
becquerel, donner son symbol.
L'activité, nombre de désintégraions par seconde, s'exprime en
becquerel ( Bq).
Calculer
l'activité de l'échantillon à la date t1.
N (t1) = 0,01 N0 = 10 noyaux.
A(t1 ) = l N (t1)
= 2,1112
10-6* 10 = 2,1 10-5 Bq.
En l'absence de ventillation, l'air d'une maison a une concentration
constante en radon 222.
Expliquer
pourquoi, dans certains endroits, la concentration en radon 222 reste
constante au cours du temps.
Dans un endroit peut
ventilé, situé dans une région granitique, le radon 222 se forme
par une succession de désintégrations radioactives ; d'autre part le
radon est lui même radioactif, il se désintègre en polonium 218.
Expliquer
le principe de la datation pour une espèce radioactive.
De toutes les méthodes radio-chronologiques
( basées sur la loi statistique de Curie-Rutherford-Soddy ou loi de
décroissance radioactive), celle de la datation au carbone 14 est la
plus connue. Dans la haute atmosphère, soumis au rayonnement cosmique
galactique constitué de protons, des neutrons secondaires interagissent
avec les noyaux d'azote 14. Cette réaction forme un isotope AZX
du carbone : le fameux carbone 14.
Immédiatement formé le carbone 14 s'oxyde en se combinant avec
l'oxygène pour former du dioxyde de carbone qui se mélange avec le
reste de l'atmosphère. Or le carbone 14 est radioactif. La teneur en
carbone 14 est constante dans le monde ( dans l'atmosphère comme dans
chaque organisme vivant ). Cela est du à un équilibre entre la
désintégration et la production de carbone 14. Chaque gramme de carbone
contient des atomes de carbone 14. On enregistre en moyenne 13,5
désintégrations par minute et par gramme de carbone. Lorsqu'un arbre,
par exemple, est abattu, le bois cesse de vivre, le processus de
photosynthèse s'arrête et il n'y a plus d'absorption de dioxyde de
carbone. Le carbone 14 est alors libre de se désintégrer sans
compensation. On peut donc dater l'âge de la mort de l'organisme ( au
moment où cesse tout échange de CO2 avec l'atmosphère).
La mesure
de la concentration en radon 222 dans l'air des poumons d'une personne
décédée dans un tel lieu, permettrait-elle de connaîte précisément la
date du décès ?
Oui si le décès n'est pas antétieur à 5 demi-vie radioactive du radon
222 ( soit environ 19 jours). Au delà, il reste trop peu de
raddon 222 dans les poumons.
Calculer
en J et en MeV, l'énergie libérée par la désintégration d'un noyau
de radon
222.
Dm = m(21884Po)
+ m(42He) - m(22286Rn) =
217,9629 + 4,002 - 221,9704 = -0,0055 u
-0,0055 * 1,66054 10-27 = -9,13297 10-30 kg
;
E = | Dm|c2 =
9,13297 10-30* (3,00 108 )2 =8,22 10-13 J.
8,22 10-13 / 1,60 10-13 = 5,14 MeV.
Oscillations
à la surface de l'eau.
On
étudie un bouchon de forme cylindrique, de rayon r = 2,00 cm et de
hauteur h = 10,0 cm. Le bouchon est homogène de masse volumique µ =750
kg m-3. Dans tout l'exercice on suppose que le bouchon reste
vertical. On repère son cente de gravité par l'abscisse x. L'axe Ox
étant vertical dirigé vers le haut. On donne g = 9,81 m s-2.
Dans cette partie, on place le bouchon dans un liquide de masse
volumique µL. Le bouchon est immobile et flotte.
Faire un
bilan des forces s'exerçant sur le bouchon et les faire figurer sur un
schéma sans souci d'échelle.
Le
bouchon est soumis à son poids , vertical, vers le bas, valeur mg et à
la poussée d'Archimède, verticale, vers le haut, égale au poids du
volume de liquide déplacé.
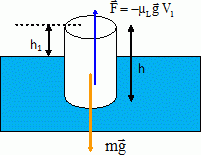
La partie émergée ( hors de l'eau ) du bouchon représente une hauteur h1
= 2,25 cm.
Exprimer µL
en fonction de µ, h et h1. Calculer µL.
V = p r2 h
; m = µV = µp r2 h ; P = mg = µ p r2 hg.
V1 = p r2 (h-h1
); F = µLgV1 = µL
p r2 (h-h1 ) g.
A l'équilibre, les forces se compensent :
µ p r2 hg = µL p r2 (h-h1 ) g.
µ h = µL (h-h1 )
; µL =
µ h /(h-h1 ) = 750 *10 / 7,75 = 968 kg m-3.
Dans cette
partie le bouchon n'est plus immobile. On l'immerge verticalement dans
l'eau de masse volumique µeau = 1000 kg m-3.
A la date t=0, on l'enfonce de façon à ce qu'il ne reste plus qu'un
centimètre hors de l'eau et on le lâche sans vitesse initiale.
L'origine de l'axe, x=0, correspond au centre de gravité dans la
position d'équilibre.
Déterminer la valeur
X0 de x à la date t=0.
Le bouchon est enfoncé de 1,25 cm : X0 = - 1,25 cm.
Pour
une position quelconque, déterminer l'expression de la poussée
d'Archimède exercée par l'eau sur le bouchon en fonction de x.
Hauteur immergée : ½h +2,75 -x = 5+2,75-x = 7,75 - x cm =
(7,75-x ) 10-2 m.
Volume immergé : p r2 (7,75-x ) 10-2 ; poussée
: µeau p r2
(7,75-x ) 10-2 g.
On néglige les frottements.
Montrer
que l'équation différentielle peut se mettre sous la forme x" +w02x = A où w0 et A sont des
constantes.
Poids mg avec m = µ
p
r2 h.
Ecrire la seconde loi de Newton sur l'axe Ox :
-µ p r2
h g +µeau p r2
(7,75-x ) g = m x" = µ p r2 h x".
-µ h g +µeau (7,75-x
) g = µ h x".
x" + µeau / (µ h) g x =( 7,75 µeau / ( µ h) -1 ) g.
On pose w02 =µeau / (µ h)
g = 1000 *9,81 / (750*0,1) =130,8
rad2 s-2.
On pose A = ( 7,75
µeau / ( µ h)
-1 ) g = (7,75*1000/ (750*10)-1)*9,81 =0,327 m s-2.
|
On se place dans des conditions telles
que A =0.
Montrer
que x(t) = Xm cos ( 2p/T0
t + F) est solution de
l'équation différentielle.
w0 = 2p/T0 ; x'(t) = Xm(-w0
) sin ( w0
t +F) ; x"(t) = Xm(-w20
) cos ( w0
t +F) = -w20 x(t).
Repport dans l'équation différentielle : -w20
x(t)+ w20 x(t) = 0.
Cette égalité est vérifiée quel que soit t : x(t) est bien solution de
l'équation différentielle.
Le mouvement du bouchon est rectiligne sinusoïdal non amorti. (
oscillateur harmonique )
Comment nomme t-on Xm,
T0 et F ? Déterminer ces
grandeurs.
Xm : amplitude positive ; T0 : période propre ; F : phase à l'origine.
Xm
= 1,25 cm ; T0 = 2p
/ w0 avec w0
= 11,44 rad/s. T0 =6,28 / 11,44 = 0,549 s.
x(0) = -1,25 = 1,25 cos F
; cos F = -1 ; F
= p rad.
Donner
l'expression de la vitesse au cours du temps. En déduire la valeur de
la vitesse au passage à la position 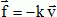 d'équilibre. d'équilibre.
x(t) = Xm cos( w0
t +F) ; au premier passage à la
position d'équilibre : 0 = Xm cos( w0
t +F) ; w0
t +F = -½p.
w0 t = -½p- (-p) = ½p ; t = ½p /w0 = 0,25 T0.
v(t)
= x'(t) = Xm(-w0 ) sin ( w0
t +F)
Au passage à la position d'équilibre : v = Xm(-w0
) sin( ½p -p) = w0
Xm =
11,44 * 0,0125 =0,143 m/s.
On tient compte à présent des frottements de l'eau sur le bouchon. La
force de frottement a pour expression 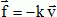 où v représente la vitesse. où v représente la vitesse.
Quelle est l'unité
de k ?
k est une force divisée par une vitesse ; une
force est une masse fois une accélération :
[ f ] = M L T-2 ; [v] = L T-1 ; [k ] = M T-1
; k s'exprime en kg s-1.
Ecrire
la nouvelle équation différentielle du mouvement en tenant compte de la
force de frottement.
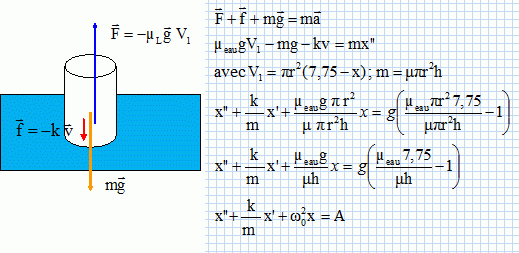
Il s'agit d'un mouvement
pseudopériodique. L'amplitude des oscillations diminue au cours du
temps.
|
|
Donner la
composition du noyau de radon 222.
Z = 86 ; 86 protons et 222-86 = 136 neutrons.
Le radon 222 est issu du noyau de radium 226
Ecrire l'équation de
cette désintégration. De quel type de radioactivité s'agit-il ?
22688Ra ---> 22286Rn
+ 42He, radioactivité de type alpha.
Donner les deux
autres types de radioactivité en précisant le nom de la particule émise.
Radioactivité de type ß- : émission
d'un électron.
Radioactivité de type ß+ : émission
d'un positon.
Ecrire l'équation de
désintégration du radon 222.
22286Rn
---> 21884Po+ 42He.
Au cours de la désintégration du radon 222, on observe l'émission d'un
rayonnement g.
Définir
cette émission. Quel noyau émet ce rayonnement ?
Le rayonnement g est un
photon, de même nature que la lumière, mais beaucoup plus énergétique.
Le noyau fils 21884Po, se trouve souvent dans un
état excité : lors du retour à l'état fondamental, il libère son
surplus d'énergie sous forme de photon g.
|
On considère un échantillon
contenant à la date t=0, N0 = 1000 noyaux de radon 222.
Calculer
la constante radioactive du radon.
l = ln2 / t½
avec t½ = 3,8 *24*3600 =3,2832 105 s.
l = ln2 / t½ = ln 2 / 3,2832 105= 2,1112 10-6 ~2,1 10-6 s-1.
Ecrire
la loi de décroissance radioactive de l'échantillon. Tracer la courbe
N=f(t) en faisant apparaître la demi-vie.
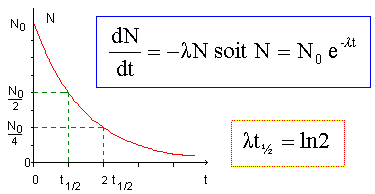
|
A quelle date t1,
il ne reste plus que 1% du nombre initial de noyaux ?
N = 0,01 N0 = N0 exp(-lt1) avec l = ln2 / 3,8 = 0,1824 jour-1.
ln 0,01 = -0,1824 t1
; t1 = 25,2 ~ 25
jours.
Définir l'unité le
becquerel, donner son symbol.
L'activité, nombre de désintégraions par seconde, s'exprime en
becquerel ( Bq).
Calculer
l'activité de l'échantillon à la date t1.
N (t1) = 0,01 N0 = 10 noyaux.
A(t1 ) = l N (t1)
= 2,1112
10-6* 10 = 2,1 10-5 Bq.
En l'absence de ventillation, l'air d'une maison a une concentration
constante en radon 222.
Expliquer
pourquoi, dans certains endroits, la concentration en radon 222 reste
constante au cours du temps.
Dans un endroit peut
ventilé, situé dans une région granitique, le radon 222 se forme
par une succession de désintégrations radioactives ; d'autre part le
radon est lui même radioactif, il se désintègre en polonium 218.
Expliquer
le principe de la datation pour une espèce radioactive.
De toutes les méthodes radio-chronologiques
( basées sur la loi statistique de Curie-Rutherford-Soddy ou loi de
décroissance radioactive), celle de la datation au carbone 14 est la
plus connue. Dans la haute atmosphère, soumis au rayonnement cosmique
galactique constitué de protons, des neutrons secondaires interagissent
avec les noyaux d'azote 14. Cette réaction forme un isotope AZX
du carbone : le fameux carbone 14.
Immédiatement formé le carbone 14 s'oxyde en se combinant avec
l'oxygène pour former du dioxyde de carbone qui se mélange avec le
reste de l'atmosphère. Or le carbone 14 est radioactif. La teneur en
carbone 14 est constante dans le monde ( dans l'atmosphère comme dans
chaque organisme vivant ). Cela est du à un équilibre entre la
désintégration et la production de carbone 14. Chaque gramme de carbone
contient des atomes de carbone 14. On enregistre en moyenne 13,5
désintégrations par minute et par gramme de carbone. Lorsqu'un arbre,
par exemple, est abattu, le bois cesse de vivre, le processus de
photosynthèse s'arrête et il n'y a plus d'absorption de dioxyde de
carbone. Le carbone 14 est alors libre de se désintégrer sans
compensation. On peut donc dater l'âge de la mort de l'organisme ( au
moment où cesse tout échange de CO2 avec l'atmosphère).
La mesure
de la concentration en radon 222 dans l'air des poumons d'une personne
décédée dans un tel lieu, permettrait-elle de connaîte précisément la
date du décès ?
Oui si le décès n'est pas antétieur à 5 demi-vie radioactive du radon
222 ( soit environ 19 jours). Au delà, il reste trop peu de
raddon 222 dans les poumons.
Calculer
en J et en MeV, l'énergie libérée par la désintégration d'un noyau
de radon
222.
Dm = m(21884Po)
+ m(42He) - m(22286Rn) =
217,9629 + 4,002 - 221,9704 = -0,0055 u
-0,0055 * 1,66054 10-27 = -9,13297 10-30 kg
;
E = | Dm|c2 =
9,13297 10-30* (3,00 108 )2 =8,22 10-13 J.
8,22 10-13 / 1,60 10-13 = 5,14 MeV.
Oscillations
à la surface de l'eau.
On
étudie un bouchon de forme cylindrique, de rayon r = 2,00 cm et de
hauteur h = 10,0 cm. Le bouchon est homogène de masse volumique µ =750
kg m-3. Dans tout l'exercice on suppose que le bouchon reste
vertical. On repère son cente de gravité par l'abscisse x. L'axe Ox
étant vertical dirigé vers le haut. On donne g = 9,81 m s-2.
Dans cette partie, on place le bouchon dans un liquide de masse
volumique µL. Le bouchon est immobile et flotte.
Faire un
bilan des forces s'exerçant sur le bouchon et les faire figurer sur un
schéma sans souci d'échelle.
Le
bouchon est soumis à son poids , vertical, vers le bas, valeur mg et à
la poussée d'Archimède, verticale, vers le haut, égale au poids du
volume de liquide déplacé.

La partie émergée ( hors de l'eau ) du bouchon représente une hauteur h1
= 2,25 cm.
Exprimer µL
en fonction de µ, h et h1. Calculer µL.
V = p r2 h
; m = µV = µp r2 h ; P = mg = µ p r2 hg.
V1 = p r2 (h-h1
); F = µLgV1 = µL
p r2 (h-h1 ) g.
A l'équilibre, les forces se compensent :
µ p r2 hg = µL p r2 (h-h1 ) g.
µ h = µL (h-h1 )
; µL =
µ h /(h-h1 ) = 750 *10 / 7,75 = 968 kg m-3.
Dans cette
partie le bouchon n'est plus immobile. On l'immerge verticalement dans
l'eau de masse volumique µeau = 1000 kg m-3.
A la date t=0, on l'enfonce de façon à ce qu'il ne reste plus qu'un
centimètre hors de l'eau et on le lâche sans vitesse initiale.
L'origine de l'axe, x=0, correspond au centre de gravité dans la
position d'équilibre.
Déterminer la valeur
X0 de x à la date t=0.
Le bouchon est enfoncé de 1,25 cm : X0 = - 1,25 cm.
Pour
une position quelconque, déterminer l'expression de la poussée
d'Archimède exercée par l'eau sur le bouchon en fonction de x.
Hauteur immergée : ½h +2,75 -x = 5+2,75-x = 7,75 - x cm =
(7,75-x ) 10-2 m.
Volume immergé : p r2 (7,75-x ) 10-2 ; poussée
: µeau p r2
(7,75-x ) 10-2 g.
On néglige les frottements.
Montrer
que l'équation différentielle peut se mettre sous la forme x" +w02x = A où w0 et A sont des
constantes.
Poids mg avec m = µ
p
r2 h.
Ecrire la seconde loi de Newton sur l'axe Ox :
-µ p r2
h g +µeau p r2
(7,75-x ) g = m x" = µ p r2 h x".
-µ h g +µeau (7,75-x
) g = µ h x".
x" + µeau / (µ h) g x =( 7,75 µeau / ( µ h) -1 ) g.
On pose w02 =µeau / (µ h)
g = 1000 *9,81 / (750*0,1) =130,8
rad2 s-2.
On pose A = ( 7,75
µeau / ( µ h)
-1 ) g = (7,75*1000/ (750*10)-1)*9,81 =0,327 m s-2.
|
On se place dans des conditions telles
que A =0.
Montrer
que x(t) = Xm cos ( 2p/T0
t + F) est solution de
l'équation différentielle.
w0 = 2p/T0 ; x'(t) = Xm(-w0
) sin ( w0
t +F) ; x"(t) = Xm(-w20
) cos ( w0
t +F) = -w20 x(t).
Repport dans l'équation différentielle : -w20
x(t)+ w20 x(t) = 0.
Cette égalité est vérifiée quel que soit t : x(t) est bien solution de
l'équation différentielle.
Le mouvement du bouchon est rectiligne sinusoïdal non amorti. (
oscillateur harmonique )
Comment nomme t-on Xm,
T0 et F ? Déterminer ces
grandeurs.
Xm : amplitude positive ; T0 : période propre ; F : phase à l'origine.
Xm
= 1,25 cm ; T0 = 2p
/ w0 avec w0
= 11,44 rad/s. T0 =6,28 / 11,44 = 0,549 s.
x(0) = -1,25 = 1,25 cos F
; cos F = -1 ; F
= p rad.
Donner
l'expression de la vitesse au cours du temps. En déduire la valeur de
la vitesse au passage à la position 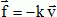 d'équilibre. d'équilibre.
x(t) = Xm cos( w0
t +F) ; au premier passage à la
position d'équilibre : 0 = Xm cos( w0
t +F) ; w0
t +F = -½p.
w0 t = -½p- (-p) = ½p ; t = ½p /w0 = 0,25 T0.
v(t)
= x'(t) = Xm(-w0 ) sin ( w0
t +F)
Au passage à la position d'équilibre : v = Xm(-w0
) sin( ½p -p) = w0
Xm =
11,44 * 0,0125 =0,143 m/s.
On tient compte à présent des frottements de l'eau sur le bouchon. La
force de frottement a pour expression 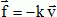 où v représente la vitesse. où v représente la vitesse.
Quelle est l'unité
de k ?
k est une force divisée par une vitesse ; une
force est une masse fois une accélération :
[ f ] = M L T-2 ; [v] = L T-1 ; [k ] = M T-1
; k s'exprime en kg s-1.
Ecrire
la nouvelle équation différentielle du mouvement en tenant compte de la
force de frottement.
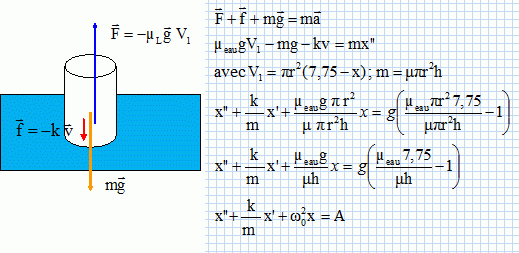
Il s'agit d'un mouvement
pseudopériodique. L'amplitude des oscillations diminue au cours du
temps.
|
|



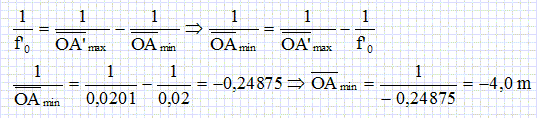


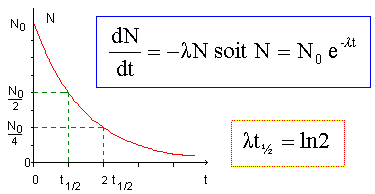
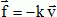 d'équilibre
d'équilibre