Le golf urbain : concours audioprothésiste Paris 2010. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

Lors d'une partie, un coup se déroule sur une péniche. le but du coup est  de rentrer directement la balle dans le trou situé à l'autre extrémité de la péniche ou de s'en approcher au maximum. Pour simplifier l'exercice on considèrera que la péniche est animé d'un mouvement  horizontal rectiligne uniforme ( V1 = 10 m/s) par rapport à la berge. Le référentiel lié à la péniche est galiléen. Le sol de la péniche est horizontal ; le champ de pesanteur terrestre est uniforme. On néglige tout frottement, toute action de l'air sur la balle, et tout effet particulier donné à celle-ci. g = 10 m s-2 ; masse de la balle m = 46 g. On assimilera la balle à son centre de gravité G. Les jouerurs pratiquent ce golf urbain avec un seul club, un fer 9, qui a pour caractéristique de donner à la vitesse initiale un angle avec l'horizontal a = 50°. Coup classique. La balle quitte le sol de la péniche avec une vitesse initiale v0 faisant un angle a avec l'horizontale et se trouve en A à une hauteur d0 = 2,0 cm au dessus du sol. Le point de départ A de la balle sera pris comme origine du mouvement L'origine du repère O est sur le sol de la péniche à la verticale de A. Montrer que le mouvement de G est uniformément accéléré, si on néglige la résistance de l'air. Référentiel galiléen lié au bateau ; le système est la balle . La balle n'est soumise qu'à son poids. La seconde loi de Newton  donne : 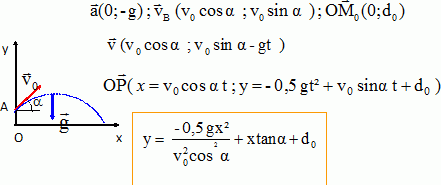Etablir dans le repère lié à la péniche les équations horaires et l'équation de la trajectoire. ( voir ci-dessus ).   Quelle est l'altitude maximale atteinte ? ( expression littérale). flèche : Au sommet de la trajectoire , le vecteur vitesse est horizontal : la composante suivant Oy est nulle. D' où tS= v0sin a / g. Puis on remplace le temps dans l'expression donnant l'ordonnée y et x. d'où : xS=v0 cos a v0sin a / g =v0² sin acos a / g = ½v0² sin (2a)/ g. yS= -½g(v0sin a / g)² + v0sina v0sin a / g +d0= ½v0²sin² a / g +d0.   Le trou cible est situé sur le sol de la péniche et à  un distance d = 90 m du départ, quelle vitesse le joueur doit-il communiquer à la balle pour tomber directement dans le trou. On donnera l'expression littérale puis la valeur numérique. portée : Lorsque le boulet retombe sur le sol horizontal, y=0, l'abscisse est égale à la portée d. 0 = -½ gd² /(v0²cos²a) + d sin a / cosa +d0. Multiplier par cos a et diviser par d : 0= -½gd/(v0²cosa) + sin a + d0 / d cos a. gd / (v0²cosa) = 2sin a+ 2d0 / d cos a. v0²cosa =gd /(2sin a+ 2d0 / d cos a) v02 =gd /(sin (2a)+ 2d0 / d cos2 a) ; v0 =(gd /(sin (2a)+ 2d0 / d cos2 a))½. v0 = (10*90/ ( sin 100 +0,04 cos250 / 90)) ½ =30,23 ~30 m/s. Quelle est la durée du vol de la balle ? d = v0 cos a t ; t =d / (v0 cos a) = 90 /(30,23 *cos 50)= 4,632 ~4,6 s. Pour compliquer le coup. Les joueurs décident d'intégrer une contrainte suplémentaire : la balle doit passer au dessus d'une passerelle placée au dessus du fleuve pour retomber ensuite sur le bateau. On considère maintenant que toutes les balles sont envoyées de façon identique avec une vitesse initiale faisant l'angle a avec l'horizontale et de valeur 30 m/s. La difficulté consiste donc à frapper la balle au bon moment pour que sa trajectoire passe au-dessus de la passerelle. On considère que la passerelle se trouve à une hauteur h = 10 m au dessus du sol de la péniche et on négligera sa largeur ( elle est donc assimilée à une barre horizontale ). Pour quelles valeurs de x a-t-on y supérieure à 10,0 m ? Dans le référentiel lié au bateau : -0,5 g x2 / (v02 cos2a) + x tan a + d0 > 10,0. -5x2 / (302 cos250) + x tan 50 +0,02 > 10,0. -5x2 /371,86 +1,192 x > 9,98. -0,01344 x2 +1,192 x -9,98 >0 x2 +88,65 x +744 < 0 Résoudre : les deux solutions sont x1 = 9,4 m et x2 = 79,3 m. Pour x appartenant à l'intervalle [9,4 m ; 79,3 m] y est supérieure à 10 m. Pour la valeur minimale de x, combien de temps a volé la balle ? xmin = v0 cos a t ; t =x / (v0 cos a) = 9,4 /(30 *cos 50) ~0,49 s. En déduire à quelle distance minimale de la passerelle, le joueur doit-il frapper la balle ? Dans un référentiel lié au quai : Il n'y a pas de changement sur l'axe vertical si on suppose que le quai est à la même altitude que le sol du bateau. Par contre, sur le plan horizontal, dans un référentiel lié au quai, la vitesse horizontale de la balle est : V=V1 + v0 cos a  = 10 + 30*cos 50 =29,28 m/s. La durée de vol de  la balle est inchangée pour la valeur xmin. Abscisse  de la frappe : X = V t = 29,28 *0,49 =14,3 m ~14 m avant la passerelle.

menu