Optique : lentille, doublet de lentilles, lunette afocale : concours kiné CEERRF 2011. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Pour améliorer la qualité des images données par une lentille, on  est la plupart du temps amené à l'associer à une ou plusieurs autres lentilles. Dans le cas de deux lentilles notées L1 et L2 l'association correspondante est appelée doublet de lentilles. Une telle association est alors caractérisée par la relation : 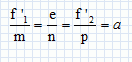f '1 et f '2 distances focales images des deux lentilles. e : distance entre L1 et L2 ou épaisseur du doublet. a : longueur qui fixe l'échelle du doublet ( ou échelle du doublet ). m, n, p sont 3 nombres algébriques entiers, sans unité. On utilisera les deux lentilles se trouvant dans un doublet ( m=4 ; n =3 ; p =1 ). Exprimer en fonction des données les distances focales images des deux lentilles, la distance entre les deux lentilles. Etablir l'expression de l'intervalle optique ( distance algébrique entre le foyer principal image de L1 et le foyer objet de L2), noté D, en fonction de l'échelle du doublet. f '1 = m a  = 4 a ; f '2 = p a = a ; e = n a = 3 a. 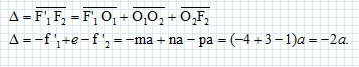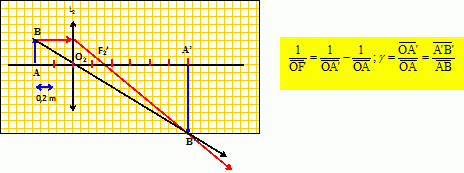Un doublet de lentille est qualifié d'achromatique s'il vérifie la relation f '1 +f '2 = 2e.   Ce doublet est-il achromatique ?   f '1 +f '2 =m a +p a = 4a+a = 5 a ; 2e = 6 a. Ce doublet n'est pas achromatique. On étudie la lentille L1 seule. Cette lentille donne d'un objet réel, une image telle que : , deux fois plus grande que l'objet. Rappeler les formules de conjugaison et de grandissement de Descartes. A quelles conditions ces formules sont-elles applicables ? L'objet est de petites dimensions etplacé au voisinage de l'axe optique principal. On élimine (utiliser un diaphragme) les rayons lumineux trop inclinés sur l'axe optique principal. Les lentilles, qui fonctionnent dans ces conditions, sont stigmatiques : tout faisceau issu d'un point lumineux donne à la sortie du système optique, un faisceau convergeant en un point, ou semblant provenir d'un point. Dans le cas considéré, quel est le signe du grandissement ? Justifier. 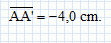est négatif, le point A' est à gauche du point A. Or l'objet est réel, il se situe donc à gauche de la lentille.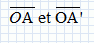 sont tous deux négatifs et le grandissement transversal est positif. Etablir l'expression littérale de  la distance focale image de la lentille L1. Calculer sa valeur. 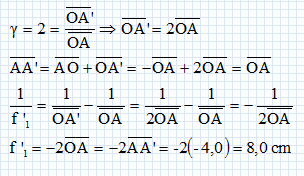En déduire la valeur numérique de l'échelle du doublet puis celle de f '2. f '1 = 4 a = 8,0 cm d'où a = 2, 0 cm ; f '2 = a = 2,0 cm. Faire une construction à l'échelle  ( objet réel situé à 8,0 cm à droite de la lentille ). Donner les 3 caractéristiques de l'image. L'image est réelle, droite, plus petite que l'objet. On souhaite  maintenant associer la lentille L1 avec la lentille L2 de façon à obtenir un système afocal. 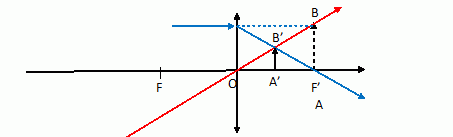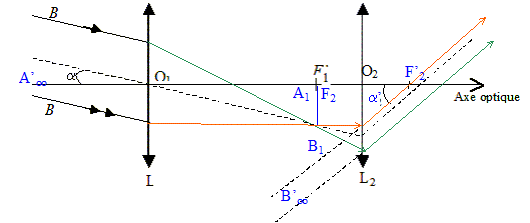Que signifie le terme afocal ? L'objectif de cette lunette, donne d'un objet AB très éloigné (considéré à l'infini), une image intermédiaire A1B1 située entre l'objectif et l'oculaire. L'oculaire qui sert à examiner cette image intermédiaire, en donne une image définitive A'B'. Lorsque cette image définitive est à l'infini, la lunette est dite afocale. La distance e du doublet ainsi constitué pat L1 et L2 satisfait-il à cette condition ? Sinon quelle doit être sa valeur ? F'1 et F2 sont confondus ; e = f '1 + f '2 ; e =n a = 3 a ;  f '1 + f '2  = (m +p )a = 5 a. La condition e = f '1 + f '2  n'est pas respectée. Il faudrait que la distance des deux lentilles soit égale à 10 cm. Un observateur emmétrope ( oeil normal)  souhaite voir avec l'association ainsi réalisée un objet très éloigné. Faire un schéma de principe. ( voir ci dessus ). Faire apparaître a, diamètre apparent de l'objet et a', diamètre apparent de l'image. Les exprimer dans le cadre de l'approximation des petits angles. Définir le grossissement de cette association, l'exprimer et le calculer. La lunette est caractérisée par son grossissement G= a'/ a . tan a = A'B'/O1F1 = A'B'/ f'1 proche de a radian si l'angle est petit. tan a' = A'B' /f'2 proche de a' radian si l'angle est petit. G =  f '1 /f '2 = 8 /2 = 4,0.

menu