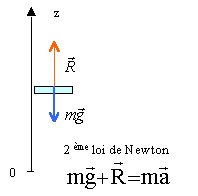Pèse personne, autour du pendule : concours Kiné Nantes 2011. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Comment varie l'indice du pèse personne ? Vous devez prévoir le sens de variation de l'indication du pèse personne pour les trois situations numérotées 2, 3, 4 en démontrant explicitement si la valeur indiquée sera supérieure, inférieure ou égale à celle de la situation 1. La même personne : 1) monte sur le pèse personne, un bâton à la main. 2) monte avec le bâton et appuie sur le pèse personne. Dans le référentiel terrestre galiléen, on considère le système { pèse personne } : le système  est en équilibre sous l'action  du sol et de l'action de la personne. D'après la première loi de Newton, ces deux forces sont opposées. L'indication en 2 est donc identique à celle lue en 1. 3) avec le bâton, il appuie sur le sol. Le poids de la personne et du bâton est réparti à la fois sur le pèse personne et le sol. L'indication lue sera inférieure à celle observée en 1. 4) Avec le bâton, il appuie au plafond. L'action exercée par le système sur le pèse personne est égale au poids augmenté de l'action du plafon sur le bâton. L'indication lue sera supérieure à celle observée en 1. Mêmes questions dans l'acenseur. La même personne, munie de son bâton est dans l'ascenseur 5) L'ascenseur est en mouvement rectiligne accéléré. Référentiel terrestre galiléen ; le système est le pèse personne. Ecrire la deuxième loi de Newton suivant l'axe z : R=ma+mg ; R= m(a+g). L'ascenseur démarre, l'accélération est positive : R est donc supérieure à mg. L'indication lue est supérieure à celle de la situation 1.   6) L'ascenseur est en mouvement rectiligne descendant ralenti. L'accélération est verticale, de sens contraire au mouvement ( la vitesse diminue ) : le vecteur accélération a le sens de l'axe. Même conclusion qu'à la question 5). 7) L'ascenseur est en mouvement rectiligne à vitesse constante. L'accélération est nulle et R = mg. L'indication lue est égale à celle de la situation 1. En impesanteur dans l'ascenseur. L'impesanteur est l'état d'un corps tel que l'ensemble des forces auquelles il est soumis possède une résultante nulle. Proposer une solution expérimentale pour que le pèse personne affiche la valeur zéro. L'ascenseur est en mouvement rectiligne, en montée, et ralentit brusquement. L'accélération est dirigée en sens contraire de l'axe. R=ma+mg ; R= m(a+g) avec a négatif. Si a+g = 0, l'indication lue est zéro. Autre situation : l'ascenseur est en chute libre. Autour du pendule. Pour toute analyse dimensionnelle d'une grandeur physique G, on notera sa dimension entre crochet telle que : (G], et qu'on ne confondra pas avec l'unité qui dépend du système de mesure choisi. On notera : [durée ] = T ; [masse] = M ; [distance ] = L ; [ intensité du courant ] = I. Un pendule est constitué d'une bille sphérique en acier de rayon r = 5,10 mm et de masse m = 200 g suspendue à un fil de lopngueur L = 62,8 cm. Cette longueur L représente la distance entre le point de fixation O du fil et le centre de l'objet. On note la valeur moyenne du champ de pesanteur à la surface de la terre gT = 9,81 SI. et la valeur du champ de pesanteur à la surface de la lune gL=1,62 SI. Le champ gravitationnel est inversement proportionnel au carré de la distance qui sépare les centres d'inertie des deux corps massiques. Description du pendule réel. On considère que la masse du fil est très inférieure à celle de la bille. Une modélisation élaborée permet d'obtenir l'expression suivante pour la période temporelle T1. A l'aide d'une analyse dimensionnelle, montrer l'homogénéité de cette formule. [m r2]=M L2 ; [m L2]=M L2 ;  [2/5m r2+m L2 ]= M L2 ; [mgL] = M L T -2L = M L2T -2 ; [(2/5m r2+ m L2) / (mgL)] =T2 ; [((2/5m r2+ m L2) / (mgL))½] =T ; la période T1 est homogène à une durée. Déterminer la valeur de T1 dans l'unité SI sur terre. T1 = 2 p ((0,4 r2+  L2) / (gL))½ = 6,28* ((0,4 *(5,10 10-3)2+  0,6282) / (9,81*0,628))½ = 1,59 s. Vérifier que (r/L)2 < 0,001, montrer que T1 se réduit à la période propre d'un pendule simple. (5,10 10-3 / 0,628)2 =6,6 10-5. En 1671, Richer, un astronome français, part pour Cayenne en Guyanne pour effectuer un pointé précis de la planète Mars ainsi que la distance Terre-Mars. Mais en réalisant ses expériences, il fait une découverte inattendue : en réglant ses horloges, il constate en effet que le même pendule bat plus lentement à Cayenne qu'à Paris. ( d'après Newton et la mécanique céleste ). Que peut-on dire de la période du pendule utilisé à Cayenne appelée TC par rapport à la période de ce même pendule utilisé à Paris ? Si le même pendule bat plus lentement à Cayenne quà Paris, alors TC > T1. Quelle grandeur physique peut expliquer cette observation ? La longueur du pendule est inchangée, c'est donc la valeur du champ de pesanteur terrestre qui varie entre Paris et Cayenne. Qu'avait pu en conclure Richer sur la longueur du rayon terrestre au pôle et à l'équateur de la terre ? La période du pendule est proportionnelle à g-½. L'accélération g est proportionnelle à l'inserse du carré d'une distance distance. La période est donc proportionnelle à une distance. TC > T1 conduit à : le rayon terrestre à l'équateur est supérieur au rayon terrestre à Paris ( et donc au pôle ). Mesures liées au pendule réel. Ci dessous le graphe de l'abscisse angulaire q(t) en radian en fonction du temps du pendule lâché sans vitesse initiale. Evaluer l'intervalle de temps entre chaque mesure en explicitant votre méthode. Dans la partie linéaire du graphe, on peut compter 20 intervalles de temps pour environ 0,40 s : 0,40 / 20 ~0,020 s.  Si vous deviez réaliser manuellement une mesure le plus précisément possible de la période du pendule, comment procéder expérimentalement avec l'usage de matériels simples que vous indiquerez ? Le longueur du pendule est mesurée à l'aide d'une grande règle ou d"un mètre. L'angle initial est mesuré à l'aide d'un rapporteur. On mesure la durée de 10 oscillations puis on divise par 10 pour trouver la période. Approximation du pendule réel pour le cas des petits angles. Pour les petits angles on peut écrire sin q ~q en radian si l'écart est inférieur à 1 %. Calculer le rapport (q-sinq) / q exprimé en pourcentage pour les valeurs suivantes :1,00 10-1 rad ; 2,00 10-1 rad ; 2,50 10-1 rad. 100 (0,1 - sin 0,1) / 0,1 = 0,17 % ; 100 (0,2 - sin 0,2) / 0,2 = 0,67 % ; 100 (0,25 - sin 0,25) / 0,25 = 1,04 ; l'enregistrement ci-dessus est réalisé avec un écart angulaire maximal de 0,15 rad. Le rapport (q-sinq) / q est inférieur à 1% et l'approximation des petits angles est donc réalisée. Comment montrer expérimentalement l'influence de l'angle sur la période ? La longueur L étant constante, mesurer la période pour des valeurs croissantes de l'écart angulaire initial. Par exemple de 10 en 10 degrés. Pour les petits angles, la période est constante ; par contre elle augmente pour les écarts angulaires initiaux supérieurs à 30°. Modélisation du pendule réel par un pendule simple. Dans l'approximation étudiée ci-dessus et en négligeant les frottements dans l'air, ainsi que la poussée d'Archimède dans le fluide air, l'expression de l'abscisse angulaire s'écrit : q(t) = qm cos (2p t / T0 +f). Que représentent les grandeurs qm et f ? qm  : amplitude angulaire ;  f : phase à l'origine. Déterminer graphiquement  qm et f en degré, ainsi que la période T0. q(0) = qm cos (f) =qm d'où cos (f) =1 et f = 0. Le dispositif oscillant est placé à la surface de la lune. Quel(s) paramètre(s) doit-on modifier et quell(s) valeur(s) doit(vent) t-il(s) prendre afin d'avoir la même période propre que sur la terre ? La période est indépendante de la masse m ; le champ de pesanteur lunaire est environ 6 fois plus petit que le champ terrestre. Il faut modifier les dimensions L et éventuellement r. Si le pendule est assimilable à un pendule simple : (r/L)2 < 0,001 soit r/L < 0,0316 ; cas limite r = 0,0316 L. T02 = 4p2 (0,4 r2 + L2) / (gLL) = 1,62 =2,56. 0,4 r2 + L2 = 2,56 *1,62 L / (4p2 ) = 0,10515 L. 0,4*( 0,0316 L)2 +L2 = 0,105 L ; L2 ~ 0,105 L ; L ~ 0,105 m et r = 0,0316*0,105 = 3,3 mm. Aspect énergétique sur terre. On rappelle les caractéristiques du pendule : L = 0,628 m et m = 200 g. L'origine de l'énergie potentielle de pesanteur est choisie à l'altitude telle que le pendule soit dans sa position de repos et l'angle initial est pris à 8,60°. L'ensemble est considéré sans frottement. Etablir l'expression de l'énergie potentielle de pesanteur du pendule en fonction de L, m, q et autre constante. Quelle est l'expression littérale de l'énergie mécanique du pendule ? Energie mécanique = énergie potentielle + énergie cinétique ; E = mgL(1-cosq) + ½mv2.   Calculer la valeur de l'énergie mécanique du système. Lorsque la vitesse est nulle, q= qm=0,15 rad ; l'énergie mécanique est sous forme potentielle. E = 0,200*9,81*0,628(1-cos0,15) =1,3836 10-2 J = 13,8 mJ. Quelle est la valeur maximale de la vitesse de la sphère ? Justifier. L'énergie mécanique se conserve. ( absence de frottement ). Au passage à la position d'équilibre l'énergie potentielle est nulle. E = ½mv2max ; vmax = (2E / m)½ = (2*1,38 10-2 / 0,2)½ = 0,372 m/s. A quelles dates prend t-elle cette valeur durant l'acquisition ? q(t) = qm cos (2p t / T0 ) = 0 ; cos (2p t / T0 ) =0 ; 2p t / T0 = 0,5 (2n+1)p  ; t = 0,25 (2n+1)T0 =0,25(2n+1)*1,6 = 0,4 (2n+1) avec n entier positif ou nul. (0,40 s ; 1,20 s ; 2,0 s ; 2,8 s ; 3,6 s ) A quelles dates, à 0,1 s près, l'énergie potentielle a-t-elle pour valeur 6,0 mJ durant l'acquisition ? 6,0 10-3 = mgL(1-cosq) = 0,2*0,628*9,81(1-cosq) =1,232(1-cosq) 1-cosq =4,87 10-3 ; cos q =0,9951 ; q = 9,873 10-2 + 2p rad et q = -9,873 10-2 + 2p rad. q(t) = qm cos (2p t / T0 )= 9,873 10-2  = 0,15 cos (2p t / T0 ) ; cos (2p t / T0 ) =9,873 10-2 / 0,15 =0,6582. 2p t / T0 = 0,8523 + np ; t = 0,8523*1,6 / 6,28 +0,8 n =0,217 + 0,8 n ( 0,2 s ; 0,2 +0,8 =1,0 s ; 0,2 +2*0,8 =1,8 s ; 0,2 +3*0,8 = 2,6 s ; 0,2 +4*0,8 = 3,4 s ) 2p t / T0 = -0,8523 + np ; t = -0,8523*1,6 / 6,28 +0,8 n = -0,217 + 0,8 n (0,6 s ;  -0,2 +2*0,8 =1,4 s ; -0,2 + 3*0,8 =2,2 s ; -0,2 +4*0,8 =3,0 s ). A la date t = 2,6 s, la bille monte-t-elle ou descend-elle ? Justifier. Quelle est la valeur de la vitesse à cette même date ? q(2,6) = qm cos (2p *2,6 / T0 ) =0,15 cos(2p *2,6 / 1,6 ) = -0,1066 rad. D'après le graphe ci-dessus, à t > 2,6 s, l'angle q est négatif et se rappro che de zéro. Donc la bille descend. ½mv2 = E-Ep ; v =(2(E-Ep) / m)½. E - mgL(1-cosq) = 13,8 10-3 -0,2*0,628*9,81(1-cos(-0,1066)) =6,8 10-3 J. v =(2*6,8 10-3 / 0,2 )½= 0,26 m/s.

Des élèves en TP décident de remplacer la bille d'acier par une boule de bois plus légère. Que devient la valeur de la période propre ? Justifier. La période propre est indépendante de la masse. La période ne change pas. L'énergie mécanique de ce nouveau pendule a-t-elle même valeur que celle du précédent ? Justifier. E = mgL(1-cosq) + ½mv2. L'énergie mécanique dépend de la masse. L'énergie mécanique change. La vitesse de passage de la bille par la position de repos est-elle la même qu'avec la bille d'acier ? Justifier. vmax = (2E / m)½ =(2gL(1-cosqm))½  ; indépendante de la masse. La vitesse maximale ne change pas.

menu