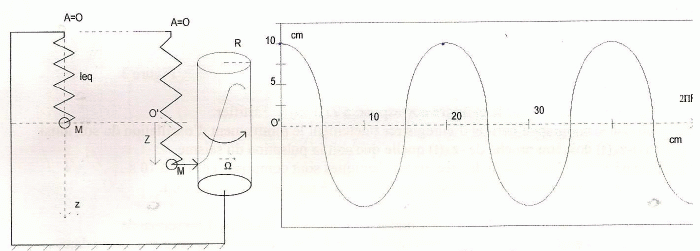
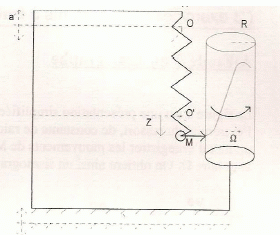
La
figure est une représentation simplifiée d'un sismographe. La masse m
accrochée à l'extrémité du ressort, de constante de raideur k, est
ponctuelle ( M). Une pointe solidaire de M permet d'enregistrer les
mouvements de M sur un cylindre, de rayon R, tournant à la vitesse
angulaire W. On obtient
ainsi sismographe.
Etude
du système en absence de secousse sismique.
Le système est à l'équilibre.
Déterminer
la longueur du ressort AM notée Léq en fonction de L0,
m, k et g.
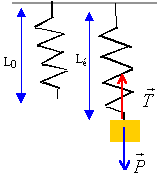
à l'équilibre : mg = k(Léq-L0) ; Léq
= mg / k +L0.
|
On
écarte la masse de sa position d'équilibre.
Déterminer
l'équation que doit satisfaire Z avec OM= Z + Léq.
Le référentiel d'étude est lié au sol.
On choisit un axe vertical orienté vers le bas, avec l'origine à la
position d'équilibre. On applique la seconde loi de Newton au
système { masse + ressort }.
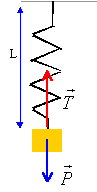
mg-k(L-l0)= m d²Z/dt²
mg-k( Léq +Z-l0)= m d²Z/dt²
mg-k( Léq -l0) - kZ =m d²Z/dt² ;
or mg = k(Léq-L0)
m d²Z/dt² + k Z=0 ; d²Z/dt² + k / m Z=0(1)
|
Montrer que Z(t)
peut s'écrire Z(t) = a sin (w0t+f). Déterminer w0 en fonction de m et
k.
Z(t)=a sin(Bt+f) ou B et f sont des constantes positives non nulles :
Calcul de B pour que Z(t)
= a sin (w0t+f) soit solution de l'équation différentielle.
Dériver deux fois Z(t) par rapport
au temps :
Z(t)
= a sin (Bt+f). Z'(t) = AB cos(Bt+f) ; Z"(t) = -AB2 sin(Bt+f) = -B2 Z(t).
Repport dans (1) : -B2 Z(t) + k / m Z(t) = 0
est vérifiée quel que soit le temps si B2= k/m
Pulsation w0 ( rad s-1) :
w0
= [k/m]½ d'où l'écriture de (1) : d²Z/dt² + w20
Z = 0 ou Z" +w20 Z =0.
(1)
Déduire
graphiquement la période d'oscillation T0.
On donne 2 p R =0,50 m et W = 0,02 rad/s.
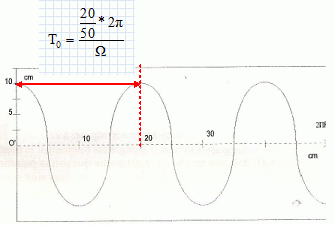
Le cylindre effectue
un tour ( 2 p R = 0,50 m )
en :
2 p / W = 2 p /0,02 = 100 p secondes.
Le
cylindre effectue 20/50=0,4 tour en T0 = 0,4 *100 p = 40 *3,14
=125,66 ~1,3 102 s.
Calculer la valeur
numérique du rapport k/m en précisant l'unité.
w0 = 2p/T0 = 6,28 / 125,66=
0,050 rad/s.
w20 = k/m = 0,052
=0,3947 ~2,5 10-3 s-2.
Etude
du système en présence de secousse sismique.
Lors d'une secousse sismique, l'extrémité du ressort A est soumise à un
mouvement d'oscillation zA(t) = a cos (wt). La position de la masse sera
toujours notée OM = Léq + Z(t).
Etablir
que l'équation que doit satisfaire Z(t) devient m Z" +kZ =kzA(t).
Tension du ressort T= k( L-L0-zA)
; mg-k( L-L0-zA)= m d²Z/dt²
; mg-k( Léq +Z-l0) + kzA= m d²Z/dt²
or mg = k(Léq-L0) ; -kZ+ kzA= m d²Z/dt²
d²Z/dt² + k/ m Z=k/ m zA (2) Cela
revient à ajouter le terme k/m zA =w20
zA au second membre de l'équation différentielle précédente.
La solution s'écrit Z(t) = Zmax cos (wt).
Exprimer Zmax en fonction de k,
a, m et w puis en fonction de
a, w et w0.
Z'(t) = -Zmax w sin (wt) ; Z"(t) = -Zmax w2 cos (wt) ;
repport dans (2) :
-Zmax w2 cos (wt) +
k/ m Zmax cos (wt) = k/m a cos (wt).
-Zmax w2 + k/ m Zmax
= k/m a.
Zmax(k/m -w2) = k/m a ; Zmax = k/m a / (k/m -w2) =a
w20
/ (w20
-w2).
Que se
passe t-il lorsque w est
proche de w0 ?
Comment appelle t-on ce phénomène ?
Si w ~w0, on observe un phénomène de résonance. L'amplitude Zmax devient
très grande.
|
|
L'enregistrement sur le cylindre
correspond à Z(t)-zA(t). Justifier .
Le cylindre d'enregistrement et le dispositif masse + ressort sont liés
au bâti du sismomètre, donc au sol.
Un mouvement du sol entraîne un mouvement du bâti, puis un
mouvement relatif entre la masse M et le bâti.
Un bon sismographe
permet d'enregistrer fidèlement le mouvement d'oscillation du sol,
ainsi Z(t)-zA(t)
doit être aussi proche de -zA(t)
quelle que soit la pulsation du séisme. Les périodes d'oscillation des
secousses sismiques sont comprises entre 1 à 10 s.
Montrer
numériquement que le sismographe étudié satisfait à cette condition.
La période propre de l'oscillateur est de l'ordre d'une centaine de
secondes, soit 10 à 100 fois plus grande que les périodes d'oscillation
des secousses.
Le ressort doit revenir le plus rapidement possible à sa position
d'équilibre ( sans osciller périodiquement) afin d'être capable
d'enregistrer les secousses suivantes. Le sismographe est équipé d'un
système d'amortissement. Le
système solide S+ ressort et amortisseur est un oscillateur
apériodique.
L'épicentre est le point source des
ondes sismiques. La planète est parsemée de sismographes.
Comment
détermine t-on l'épicentre d'un séisme ?
Ces ondes de choc se propagent en cercles concentriques à partir du
foyer et de l'épicentre, diminuant d'intensité à mesure qu'elles s'en
éloignent. Les sismomètres enregistrent les secousses à des dates
différentes. Connaissant la vitesse de propagation des ondes sismiques,
on peut déterminer la distance d entre l'épicentre et le sismomètre.
A partir de chaque sismomètre on trace des cercles de rayon d.
L'intersection des cercles donne l'épicentre.
|




