.
|
|
On se propose d’étudier, par conductimétrie, la cinétique de l’hydrolyse du 2-chloro-2-méthylpropane qui est noté RCl .
On suppose que la seule réaction qui a lieu au cours de la transformation étudiée a pour équation :
RCl (l) + 2 H2O (l) = ROH (aq) + H3O+(aq) + Cl – (aq) réaction (1)
ROH représente le 2-méthylpropan-2-ol qui est produit au cours de la transformation..
Protocole :
Le
2-chloro-2-méthylpropane (RCl) est peu soluble dans l’eau mais il est
très soluble dans un mélange eau - acétone en proportions appropriées.
Le mélange réactionnel initial est réalisé en versant une quantité de matière ni (RCl) = 9,1 10-3 mol de
2-chloro-2-méthylpropane
(RCl) dans un mélange eau – acétone. Le volume total de la solution
dans le bécher est V = 50,0 mL. L’eau présente est en très large excès.
Questions préliminaires.
On propose des affirmations concernant le taux d’avancement final d’une réaction et l’équilibre chimique.
Compléter ce tableau en répondant par VRAI ou FAUX en toutes lettres et en justifiant brièvement les
réponses.
| Vrai ou faux | Brève justification | Lorsque l'état d'équilibre est atteint, les
espèces chimiques arrêtent de réagir entre elles
au niveau microscopique. | Faux | La réaction dans le sens direct a la même vitesse
que la réaction dans le sens indirect. | Dans le cas d’un équilibre chimique,
le taux d’avancement final change si on augmente la quantité d’un réactif. | Vrai | L'équilibre est déplacé dans le sens direct, consommation du réactif ajouté. | Lorsque l’état d’équilibre chimique
d’un système est atteint, le taux
d’avancement final est toujours égal à 1. | Faux | Dans
une réaction limitée, le réactif en défaut n'est pas entièrement
consommé et le taux d'avancement final est inférieur à 1. |
Compléter le tableau d'avancement à l’aide d’expressions littérales en respectant les notations de l’énoncé. On négligera la quantité initiale d’ions H3O+ due à l’autoprotolyse de l’eau.
| Etat | avancement (mol) | RCl (l) | +2H2O(l) | =ROH (aq) | +H3O+(aq) | +Cl-(aq) | | initial | 0 | ni(RCl) | en excès | 0 | 0 | 0 | | en cours | x | ni(RCl)-x | x | x | x | | fin | xf | ni(RCl)-xf | xf | xf | xf | | état final si transformation totale | xmax | ni(RCl)-xmax | xmax | xmax | xmax |
|
.
Suivi cinétique de la transformation par conductimétrie.
La
transformation modélisée par la réaction (1) peut être suivie par
conductimétrie dans une enceinte thermostatée à la température de 40°C.
Pour
cela, on plonge dans le bécher contenant le mélange eau - acétone une
cellule conductimétrique préalablement étalonnée. On déclenche le
chronomètre à l’instant où on ajoute le 2-chloro-2-méthylpropane
(RCl) dans le mélange et on mesure la conductivité s de la solution à différentes dates.
Les résultats obtenus permettent de tracer la courbe d’évolution de l’avancement x de la réaction en fonction du temps.
On considère que l’état final est atteint à partir de la date t = 60 min.
Pourquoi peut-on effectuer un suivi conductimétrique de cette transformation ?
A
cours du temps des ions oxonium et chlorure apparaissent alors
qu'initialement il n'y avait quasiment pas d'ions. Or seuls les ions
apportent une contribution à la conductivité de la solution : celle-ci
va augmenter en cours d'évolution du système.
Courbe d’évolution temporelle de l’avancement x de la réaction.
L’expression littérale de la conductivité s d'une solution en fonction des concentrations molaires effectives [ Xi ] des ions présents dans cette solution est donnée par la relation :
s =Σ li [ Xi ] où li appelé conductivité molaire ionique est une constante dont la valeur dépend de l’ion Xi .
Donner l’expression littérale de la conductivité s de la solution en considérant que seuls les ions oxonium et chlorure, produits par la réaction (1), interviennent.
s = lH3O+ [H3O+] + lCl-[Cl-].
Déduire
l’expression de la conductivité de la solution à la date t en
fonction de l’avancement x de la réaction, du volume V de la solution
et des conductivités molaires ioniques des ions oxonium et
chlorure.
[H3O+] =[Cl-] = x / V ; s = ( lH3O+ + lCl-) x / V.
Exploitation de la courbe d’évolution temporelle de l’avancement x de la réaction.
On
rappelle l’expression de la vitesse volumique de réaction : v = 1/V
dx/dt, où V représente le volume du mélange réactionnel.
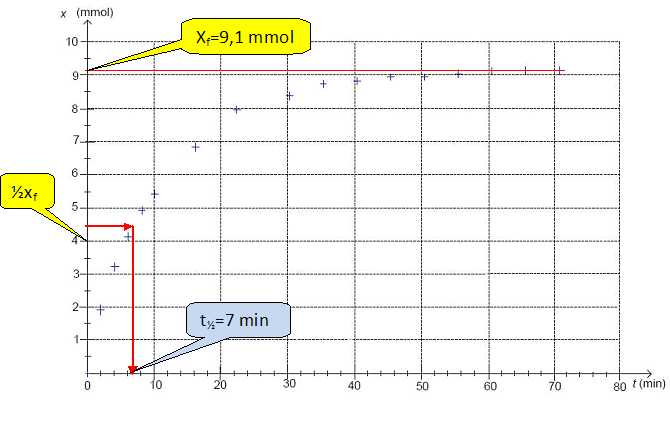
Définir le temps de demi-réaction noté t½.
Le temps de demi-réaction est la durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final.
Déterminer graphiquement t½. On fera apparaître clairement la construction graphique.
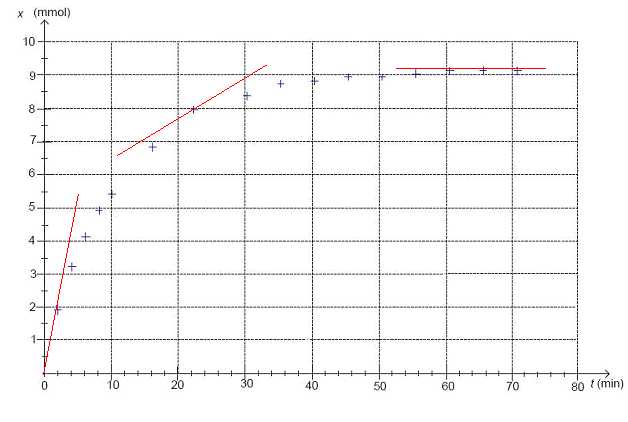
Comparer, sans nécessairement les calculer, les vitesses volumiques de réaction v0, v20 et v65 respectivement aux instants t0 = 0, t20 = 20 min et t65 = 65 min.
Justifier par un tracé graphique.
La
vitesse volumique est proportionnelle à dx/dt, pente de la tangente à
la courbe à la date t considérée. Or ces tangentes sont de moins en
moins inclinées par rapport à l'horizontale en cours d'évolution de la
transformation. la vitesse volumique diminue au cours du temps.
Quel est le facteur cinétique responsable de la variation de la vitesse volumique ? Expliquer.
Au cours du temps les concentrations des réactifs diminuent ; or la concentration d'un réactif est un facteur cinétique.
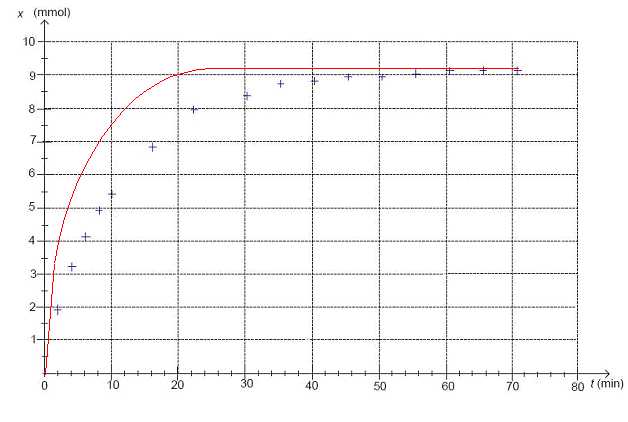
Tracer l’allure de la courbe pour une température supérieure à 40°C. Justifier.
La température est un facteur cinétique. La réaction est plus rapide, sans modification de l'état final.
|
|
|


