.
|
|
Mouvement d'une
bille.
On étudie le mouvement de chute d'une bille ponctuelle de masse m.
A la date t=0, on la lance avec une vitesse horizontale V0 =
1,8 m/s d'une hauteur H = 0,60 m. Les frottements sont négligés.
Déterminer les
coordonnées de l'accélération, de la vitesse ; en déduire les équations
horaires du mouvement et la trajectoire.
La bille n'est soumise qu'à son poids, la chute est libre.
Ecrire la seconde loi de Newton ; la vitesse est une primitive de
l'accélération ; la position est une primitive de la vitesse.
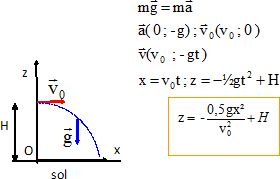
Calculer
la durée de la chute ( bille sur le sol horizontal).
z = 0 ; -½gt2 +H = 0 ; t = (2H / g)½ =(1,2 / 9,8)½
=0,35 s.
En déduire
l'abscisse xI du point d'impact.
xI = v0 t
= 1,8 *0,35 =0,63 m.
En modifiant la vitesse initiale, le point d'impact est à 0,75 m de O.
La
vitesse initiale a-telle une influence sur la durée de la chute ?
La vitesse initiale n'intervient pas dans
l'expression de la durée de la chute : t = (2H / g)½ ; elle
n'a donc pas d'influence sur cette durée.
Calculer la nouvelle
vitesse initiale v'0.
v'0 = x'I / t = 0,75 / 0,35 = 2,1 m/s.
|
.
.
Mise en orbite
d'un satellite.
G = 6,67 10-11 SI; masse de la
terre MT = 5,97 1024 kg ; rayon de la terre R =
6380 km = 6,38 106 m.
Masse de la fusée M = 180 t = 1,8 105 kg ; poussée des
moteur F = 2,25 106 N.
La poussée est constante durant l'ascension. L'étude est faite dans un
référentiel terrestre galiléen. Le champ de pesanteur est uniforme et
on néglige les effets de l'air sur la fusée.
Exprimer et calculer
l'accélération de la fusée au décollage.
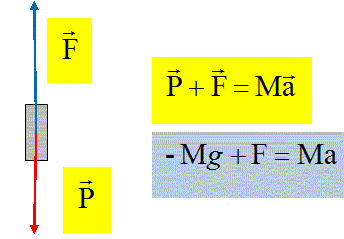
a = F / M -g = 2,25 106 / (1,8 105) -9,8 = 2,7 m s-2.
Au bout de Dt = 100 s la masse de la fusée a
diminuée de 95 tonnes.
Calculer
la nouvelle accélération de la fusée. Le mouvement est-il uniformément
accéléré ?
a1 = F / M1 -g = 2,25 106 / (8,5 104) -9,8 =16,7 ~ 17 m s-2.
L'accélération n'étant pas constante, le mouvement n'est pas uniformément accéléré.
La vitesse d'éjection des gaz est donnée par la relation 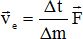 où Dt / Dm caractérise la consommation des
moteurs. où Dt / Dm caractérise la consommation des
moteurs.
Vérifier l'unité de ve par analyse dimensionnelle. Calculer ve.
Une force est une masse fois une accélération et une accélération est une distance divisée par le carré d'un temps.
[F] = M L T-2. De plus [Dt / Dm] = T M-1 ; [ve] = L T-1.
Valeur, norme de ve =| 100 /(-9,5 104 )| *2,25 106 = 2,4 103 m s-1.
Quel est le signe de Dt / Dm ? En déduire le sens de ve.
La masse de la fusée diminue : Dt / Dm est négatif. La vitesse d'éjection des gaz a le sens contraire du mouvement de la fusée.
Expliquer pourquoi l'éjection des gaz propulse la fusée vers le haut.
Le principe de l'action et de la réaction explique la propulsion des
fusées : à toute action ( éjection des gaz vers l'arrière ) correspond
une réaction égale et de sens opposé ( propulsion de la fusée ).
|
|
Etude du satellite mis en orbite.
Le satellite, de masse ms, est en orbite circulaire à l'altitude h = 650 km.
Montrer que le mouvement circulaire du satellite est uniforme.
Le satellite est soumis uniquement à la force de gravitation
centripète, perpendiculaire à chaque instant à la vitesse. Cette force
ne travaille pas et en conséquence ne modifie ni l'énergie cinétique,
ni la valeur de la vitesse du satellite.
Donner l'expression de la valeur "a" de l'accélération en fonction de la vitesse du satellite.
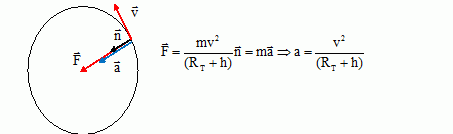
Exprimer v en fonction de GMT, R et h.

En déduire la période T de révolution en fonction de G, MT, R et h. Quelle loi de kepler retrouve-t-on ?
La période de révolution T du satellite (seconde)
est le temps mis par le satellite pour faire un tour et ce d'un mouvement
uniforme.
2 p (R+h) =vT
élever au carré, puis remplacer v² par l'expression ci dessus.
4p² (R+h) ² = v² T² = GMT/ (R+h) T²
ou T² =4p² /(GMT)(R+h)3.
soit T² /(R+h)3 = 4p² /
(GMT) rapport constant pour une planète donnée.(3ème loi de
Kepler)
|
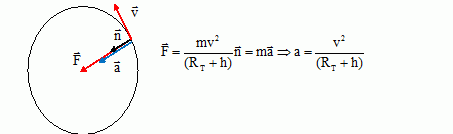

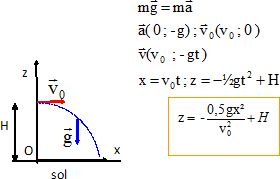
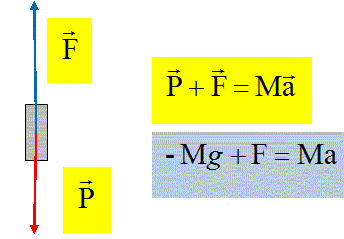
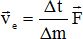 où
où