Panacées : une potion radioactive, le radithor, bac S Amérique du Nord 2012. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

De tous temps, certaines substances sont considérées comme des remèdes contre tous les maux, des panacées. Une potion radioactive. Au début du XXème siècle, le Radithor, sorte de potion magique, était censé soigner plus d'une centaine de maladies. Un cancérologue américain a trouvé chez un antiquaire plusieurs bouteilles de Radithor. Bien que vidées depuis 10 ans de leur contenu, les bouteilles se sont avétées être encore dangereusement radioactives. Chacune avait vraisemblablement contenu environ un microcurie de radium 226 et de radium 228. D'après " pour la Science " octobre 96. Un microcurie correspond à 3,7 104 Bq. Radium 226 : m( 22688Ra) = 225,977 0 u ; Radon 222 : m( 22286Rn) = 221,970 3 u ; Hélium 4 : m( 42He) = 4,001 5 u ; Radium 228 :  22888Ra ; Actinium 228 : 22889Ac. 1 u = 1,660 54 10-27 kg ; c = 3,00 108 m/s ; NA = 6,02 1023 mol-1 ; M( 22688Ra) = 226 g/mol. Le radium 226 et le mésothorium. Sur l'étiquette du Radithor est mentionnée la présence de mésothorium, ancienne dénomination du radium 228. Cette "eau certifiée radioactive" contenait également du radium 226. Les noyaux de radium 228 et de radium 226 sont des isotopes.  Expliquer. Ces deux noyaux ont le même numéro atomique Z = 88et des nombres de neutrons différents ( 228-88 = 140 et 226-88 = 138 ). Le radium 228 se désintègre pour donner l'isotope 228 de l'actinium et une particule notée X. 22888Ra ---> 22889Ac +AZX. Déterminer A et Z en citant les lois utilisées. De quel type de radioactivité s'agit-il ? Conservation du nombre de nucléons : 228 = 228 +A d'où A = 0. Conservation de la charge : 88 = 89 + Z d'où Z = -1. 22888Ra ---> 22889Ac +0-1e. Radioactivité de type ß-.   Dans la suite de l'exercice, on néglige la présence de radium 228 dans le Radithor. On suppose que l'activité radioactive du flacon est uniquement due à la présence de l'isotope 226 du radium. Celui-ci se désintègre spontanément selon l'équation : 22688Ra ---> 22286Rn + 42He. L'activité A(t) d'un échantillon de radium 226 suit la loi de décroissance exponentielle A(t) = A0 exp(-l t)  avec A0 l'activité à la date t=0. Rappeler la définition de la demi-vie t½ d'un échantillon radioactif. La demi vie est la durée au bout de laquelle l'activité initiale est divisée par deux. 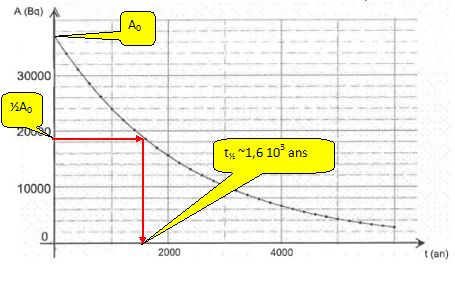Vérifier graphiquement que la demi-vie est t½ = 1,60 103 ans. Etablir la relation entre la demi-vie et la constante radioactive puis calculer sa valeur en s-1. A(t½) = ½A0 = A0 exp (-l t½) ; 0,5 = exp (-l t½) ;  ln 0,5 = -ln 2 = --l t½ ; l t½ = ln 2. l = ln2 / t½ = ln2 / (1,6 103 *365*24*3600) =1,3737 10-11 ~1,37 10-11 s-1. Donner la relation entre l'activité A(t) d'un échantillon  et le nombre N(t) de noyaux radioactifs présents. A(t) = l N(t). Calculer N0, le nombre de noyaux de radium 226 initialement présents dans un flacon de Radithor. N0 = A0 / l = 3,7 104 / (1,3737 10-11)=2,7 1015. Vérifier que le flacon contenait une masse m = 1,0 µg de radium 226. m = N0 / NA M( 22688Ra) =2,4 1015 / (6,02 1023) *226 = 1,0 106 g = 1,0 µg. . Energie libérée par le radium 226. Déterminer la variation de masse associée à la réaction de désintégration d'un noyau de radium 226. 22688Ra ---> 22286Rn + 42He. Dm = m(42He) + m(22286Rn) - m(22688Ra) = 221,970 3 +4,001 5 -225,977 0 = -5,20 10-3 u. -5,2 10-3 *1,66054 10-27 = -8,6348 10-30 ~-8,63 10-30 kg. En déduire l'énergie libérée lors de la désintégration d'un noyau de radium 226. E = Dm c2 = -8,6348 10-30  * 9,00 1016 = -7,77 10-13 J. Le signe négatif signifie que le système cède de l'énergie au milieu extérieur. Calculer l'énergie totale que peut libérer le radium 226 contenu dans un flacon de radithor. E N0 = -7,77 10-13 * 2,7 1015 =-2,1 103 J.

menu