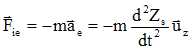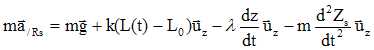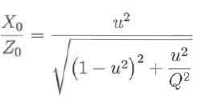|
|
Un
sismographe ou sismomètre enregistre les mouvement du sol. Pour
caractériser complètement les mouvements du sol, une station sismique
doit comporter trois sismographes, un vertical et deux horizontaux,
orientés par exemple nord-sud et est-ouest. Les périodes des ondes
sismiques varient dans une large gamm, du dixième de seconde à plus de
1000 s.
Le
système solide ressort en classe de terminale.
Proposer une
activité expérimentale en classe de terminale S permettant de
déterminer par au moins deux méthodes la constante de raideur d'un
ressort.
- Mesure de l'allongement d'un ressort vertical en fonction de la masse
accrochée. Tracer la courbe allongement = f (masse accrochée). La pente
de la droite permet d'accéder à la valeur de la raideur.
- Mesure de la période T d'un oscillateur ( masse - ressort) mécanique
vertical en fonction de la masse accrochée.
Tracer la la courbe T2 = f(masse), la pente de la droite
permet d'accéder à la raideur.
Proposer le plan
d'une séance de cours en terminale S sur le thème de la résonance
mécanique.
- Vidéos présentant le phénomène de résonance.
- Expérience : l'extrémité du ressort est reliée à un
excentrique entraîné par un moteur.
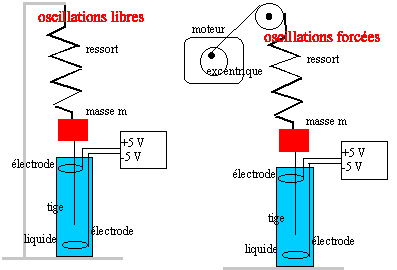
Déterminer
la fréquence propre de l'oscillateur ; faire varier la fréquence du
moteur, l'excitateur et observer l'amplitude des mouvements de la
masse. Tracer la courbe amplitude = f(fréquence).
- Définir le phénomène de résonance ; quels facteurs inluencent
la résonance ?
- Applications : rôle des amortisseurs de voitures.
- Phénomènes de résonances en électricité et en acoustique.
Sismographe simple.
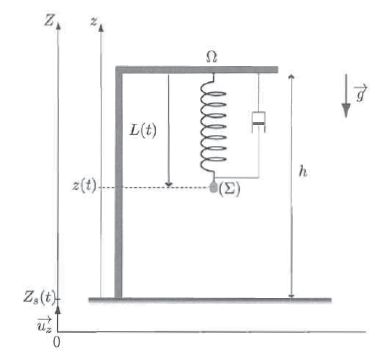
Le sismographe est constitué d'un solide de masse m suspendu à un ressort dont l'autre extrémité W
est liée à un bâti rigide solidaire du sol en vibration. Un dispositif
d'acquisition permet d'enregistrer le mouvement du solide par rapport
au bâti. On souhaite que ce mouvement reproduise le plus fidèlement
possible celui du sol par rapport au référentiel d'étude R supposé
galiléen. On appelle RS le référentiel lié au bâti rigide.
Le sol est supposé horizontal. Son mouvement vertical, lors d'une secopusse sismique sinusoïdale de pulsation w, est repéré par la cote, mesurée par rapport à R : Zs(t) = Z0 cos ( wt).
Le ressort de masse négligeable, de constante de raideur k, de longueur au repos L0,
a pour valeur L(t) à l'instant t. Un amortisseur relié au ressort,
exerce sur le solide une action mécanique modélisée par la force
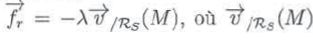 est la vitesse du solide dans le référentiel Rs. est la vitesse du solide dans le référentiel Rs.
On note L1 la longueur du ressort quand le solide est à l'équilibre en absence de secousse sismique. Le solide se situe à la cote z1 repérée par rapport au bati. La position du solide est repérée par x(t) = z(t) - z1.
|
.
.
Etablir l'équation différentielle vérifiée par x(t).
A l'équilibre le poids et la tension du ressort sont deux forces opposées : mg = k(L1-L0) avec L1 = h-z1.
z1 = h - L0-mg / k. (1)
Dans le référentiel non galiléen Rs, en translation par rapport au référentiel galiléen R, le solide S est soumis à une force d'inertie :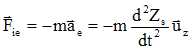
Ecrire la relation fondamentale de la dynamique apliquée au solide dans le référentiel lié au boîtier :
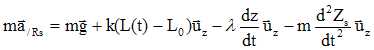
Zs(t) = Z0 cos ( wt) ; dZs(t) /dt = -wZ0 sin ( wt) ; d2Zs(t) /dt2 = -w2Z0 cos ( wt).
Projeter sur l'axe vertical : m z" = -mg +k(h-z-L0) -l z' + mw2Z0 cos ( wt).
Tenir compte de (1) : m z" = k(z1-z) -l z' + mw2Z0 cos ( wt).
Or : x(t) = z(t) - z1 d'où : x" + k/m x + l /m x' = w2Z0 cos ( wt).
En posant w02 =k/m et Q = mw0 / l = (km)½/ l : x" + w0 /Q x' + w02 x = w2Z0 cos ( wt). (2)
Donner les significations physiques et les dimensions des grandeurs w0 et Q.
Q : facteur de qualité de l'oscillateur ( sans dimension ) ; w0 : pulsation propre ( rad/s) : T-1.
On cherche la réponse du sismographe sous la forme : x(t) = X0 cos ( wt+F). On pose u = w / w0.
Montrer que : 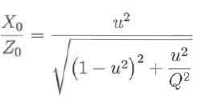
En notation complexe : x(t) =X0 exp (j F) ; x'(t) = jwX0 exp (j F) ; x"(t) = (jw)2X0 exp (j F)= -w2X0 exp (j F). Repport dans (2).
-w2X0 exp (j F) + w0 /Q jwX0 exp (j F) + w02 X0 exp (j F) = w2Z0.
Diviser par w02 : (-w2/ w02 +j w /(Qw0) +1) X0 exp (j F)= w2/ w02Z0.
(1-u2 + j u / Q) X0 exp (j F) = u2Z0.
Identifier les modules : ((1-u2)2 + u2/Q2)½ X0 = u2Z0 ; X0 /Z0 = u2/ ((1-u2)2 + u2/Q2)½.
Le graphe représentant X0 /Z0 en fonction de u, pour différentes valeurs du paramètre Q est donné :
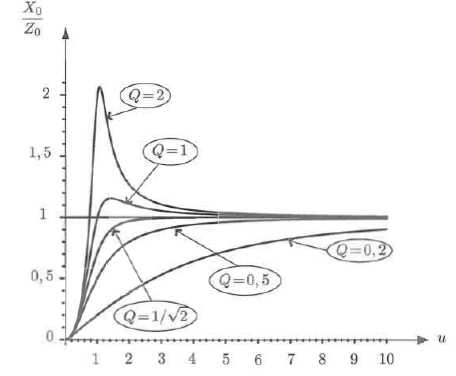
Vérifier
que l'allure de ce graphe est compatible, à haute et basse fréquence,
avec l'expression calculée. Comment peut-on qualifier ce filtre ?
A haute fréquence, u tend vers l'infini et X0 /Z0 tend vers 1. A basse fréquence, u tend vers 0 et X0 /Z0 tend vers zéro.
Le
filtre coupe les basses fréquences et laisse passer les hautes
fréquences : filtre pase haut pour les faibles valeurs de Q. Filtre
passe bande pour les valeurs élevées de Q.
On pose Y = (Z0/X0)2 et x = 1/u.
Montrer qu'il ne peut pas y avoir de résonance si Q est inférieur à une valeur limite Q0 à déterminer.
((1-u2)2 + u2/Q2 ) / u4 = Y ; Y = (1-1/u2)2 + 1/(Qu)2 ; Y = (1-x2)2 + x2/Q2 ;
Dériver Y par rapport à x et chercher la valeur de x qui annule cette dérivée :Y ' = -4x(1-x2) +2x/Q2 =0.
x = 0 et -2(1-x2) +1/Q2 =0 ; x = (1-1/(2Q2))½. 1-1/(2Q2) doit être positif ou nul : 1-1/(2Q2) >=0 ; Q =Q0 >= 1 / 2½.
Pour x = 0, Y = 1 ; pour x très grand Y tend vers l'infini ; pour Q =Q0 , Y présente un minimum et par suite X0 /Z0 présente un maximum ( résonance ).
Il ne peut pas y avoir de résonance si Q < Q0.
Comment faut-il choisir w0 par rapport à w de la secousse sismique ? Justifier.
Le mouvement du solide doit restituer le mouvement du sol : X0 = Z0 : u = w / w0 soit w >> w0.
Quel est le meilleur choix pour le paramètre Q, en termes de fidélité de la réponse et de durée du rgime transitoire ?
Pour Q = Q0, X0 /Z0 tend rapidement vers 1 pour u = 3 et de plus la durée de l'amortissement est faible.
Quel
est l'ordre de grandeur de l'allongement du ressort à l'équilibre
d'un sismographe optimisé pour détecté des ondes sismiques dont la
période est une seconde ? Commenter.
Léq-L0 = mg / k avc w02 = k / m ; Léq-L0 = g / w02 = 9,8 / (4p2)~0,25 m pour une fréquence f = 1 Hz.
Léq-L0 =9*9,8 / (4p2 )~2,2 m pour une fréquence f = 3 Hz.
Un sismographe de ce type doit avoir de très grandes dimensions.
|
.
|


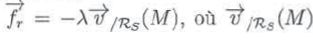 est la vitesse du solide dans le référentiel Rs.
est la vitesse du solide dans le référentiel Rs.