|
|
On
souhaite doser la quantité d'acide acétylsalicylique contenu dans un
comprimé d'aspirine. Celui-ci est dissous dans de l'eau distillée pour
donner une solution S0 de volume V0.
L'acide acétylsalicylique ( aspirine, noté HA ) a la formule ci-dessous
:
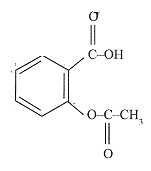
pKa
( HA / A-) = 3,6 ; 5/11,2 =0,45.
A) L'aspirine
contient une fonction anhydride d'acide. Faux.
L'aspirine
contient une fonction ester et une fonction acide carboxylique.
La solution S0 a un pH égal à 2,8.
B) L'espèce
prédominante du couple HA / A-
est la forme acide HA. Vrai.
A pH inférieur au pKa
la forme acide prédomine.
On prélève un volume Va = 5,0 mL de la solution S0
et on la dose par une solution d'hydroxyde de sodium de concentration cb
= 0,010 mol/L. le titrage est suivi par pHmétrie et on obtient la
courbe ci-dessous.
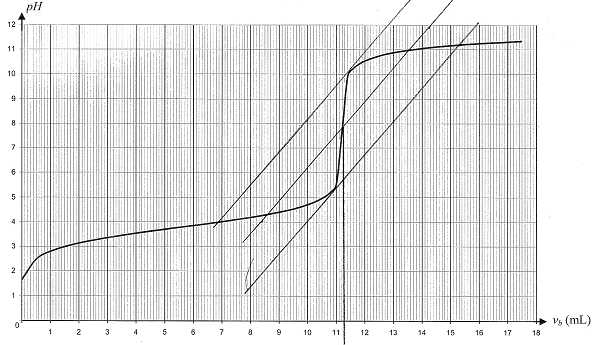
C)
L'équation de la réaction de dosage est : HA aq + HO-aq
---> A-aq + H2O(l). Vrai.
D) La concentration de la solution S0 est c0
= 0,45 mol/L. Faux.
VE = 11,2 mL, détermination
graphique.
A l'équivalence Va
c0 = VE cb
; c0 = VE
cb / Va=11,2 *0,010 / 5,0
=0,022 mol/L .
|
| .
. |
En solution aqueuse, le plomb métallique Pb et les ions
argent Ag+ réagissent pour former des ions plomb
Pb2+ et de l'argent métallique Ag.
2Ag+aq + Pb(s) = Pb2+aq
+ 2Ag(s).
A 25°C, la constante d'équilibre de cette réaction est égale à
3 1031.
On réalise le mélange, en solution aqueuse, d'une mole de plomb, d'une
mole d'argent, d'une mole d'ion argent et d'une mole d'ion plomb. On
obtient une solution de 500 mL.
A) Le quotient initial Qr i = 1. Faux.
Qr i =[Pb2+aq] / [Ag+aq ]2 avec [Pb2+aq] =[Ag+aq]= 1/0,5 = 2 mol/L ; Qr i = 2 / 22 = 0,5.
B) La réaction va s'effectuer dans le sens direct de l'équation
ci-dessus. Vrai.
Qr i < K, donc évolution dans
le sens direct.
C) La réaction peut être considérée comme quasi-totale. Vrai.
La constante
d'équilibre est très grande.
D) A l'équilibre, il y a deux moles d'argent métallique.
Faux.
A partir d'une mole de plomb, il
se forme deux moles d'argent métallique ; il y avait au départ une mole
d'argent, donc trois moles d'argent à l'équilibre.
La
réaction entre l'acide acétique et l'éthanol a un taux d'avancement à
l'équilibre de 67 % lorsque les réactifs sont en proportions
stoechiométriques.
On donne x2-4x+8/3 ~(x-0,85)(x-3,15) ;
0,67/0,3~2.
A) L'ester produit est l'éthanoate d'éthyle. Vrai.
B)
La constante d'équilibre de cette réaction s'écrit K = [ester]éq
/ ([acide]éq[alcool]éq). Faux.
K = [ester]éq [eau]éq/ ([acide]éq[alcool]éq).
C) La constante
d'équilibre de cette réaction est égale à 4. Vrai.
[ester]éq =[eau]éq = 0,67 ; [acide]éq=[alcool]éq= 0,33 ;K = 0,672/0,332
= 22 = 4.
D) Si on réalise un
mélange initial d'une mole d'acide éthanoïque et de 2 moles d'alcool,
le taux d'avancement à l'équilibre est de 85 %. Vrai.
| état |
avancement
(mol) |
acide
|
+ alcool |
= ester |
+ eau |
| initial |
0 |
1 |
2 |
0 |
0 |
| en
cours |
x |
1-x |
2-x |
x |
x |
| final |
xéq |
1-xéq |
2-xéq
= 0 |
xéq |
xéq |
K = xéq2 / ((1-xéq)(2-xéq)) = 4 ; xéq2 = 4 xéq2 -12xéq+8 ; 3 xéq2 -12xéq+8 = 0. Solution à retenir xéq = 0,85 mol.
xmax = 1 mole ( l'acide est en
défaut) ; t
= xéq/ xmax = 0,85.
On prépare la solution S en mélangeant :
0,28
g de fer en poudre, 0,56 g de cadmium, 10 mL d'une solution aqueuse de
sulfate de fer (II) de concentration 0,10 mol/L et 10 mL d'une solution
de sulfate de cadmium de concentration 0,10 mol/L.
La transformation est modélisée par l'équation chimique :
Cd2+aq + Fe(s) = Cd(s) + Fe2+aq.
La constante d'équilibre de cette réaction vaut K = 20 à 25°C. On donne 21*0,90 = 19. M(Cd) = 112 g/mol.
A) A l'équilibre l'avancement final est xf = 0,90 mmol. Vrai.
n(Fe)initial = 0,28 / 56 = 0,005 mol = 5 mmol ; n(Cd)initial = 0,56 / 112 = 0,005 mol = 5 mmol ;
n(Fe2+)initial =0,10*0,01 = 0,001 mol = 1 mmol ; n(Cd2+)initial = 0,10*0,01 = 0,001 mol = 1 mmol. ( réactif limitant xmax = 1 mmol ).
K =[Fe2+aq]éq /[Cd2+aq]éq =20 ; [Fe2+aq]éq =(1+xéq) / 20 ; [Cd2+aq]éq =(1-xéq) / 20
K =(1+xéq) /(1-xéq) = 20 ;1+xéq = 20(1-xéq) ; xéq = 19/21 =0,90 mmol.
t = xéq / xmax =0,90 / 1 = 0,90.
B) A l'équilibre la masse de cadmium a doublé. Faux.
Il se forme 0,9 mmol de cadmium ; il y avait initialement 5 mmol de cadmium ; finalement il y a 5,9 mmol de cadmium soit 0,66 g.
A l'équilibre, on ajoute au système S précédent, quelques cristaux de chlorure de cadmium. On obtient le mélange S'.
C) Le système évolue spontanément dans le sens inverse. Faux.
Qri =[Fe2+aq]initial /[Cd2+aq]initial diminue et devient inférieur à K, donc évolution dans le sens direct.
Au nouvel équilibre, on ajoute au mélange précédent un peu de poudre de fer.
D) Le système chimique reste à l'équilibre. Vrai.
Qri =[Fe2+aq]initial /[Cd2+aq]initial reste inchangé, égal à K.
|
On
désire déterminer le pourcentage massique en soude NaOH d'un déboucheur
de canalisation. On dilue 50 fois la solution commerciale de ce
déboucheur. On obtient 1,0 L de solution diluée.
On dose V=10,0 mL de cette solution par une solution d'acide chlorhydrique de concentration ca =0,10 mol/L. VE = 5,0 mL.
Données : densité du déboucheur : d = 1,1 ; 11*9 ~100 ; M(NaOH) = 40 g/mol.
A) La dilution nécessite une éprouvette graduée de 20 mL. Faux.
Fiole jaugée de 1,0 L et pipette jaugée de 1000 / 50 = 20 mL.
B) La concentration du déboucheur est 0,05 mol/L. Faux.
A l'équivalence caVE =cV ; c =caVE / V =0,10 *5,0 / 10 = 0,050 mol/L ; tenir compte de la dilution : 0,050*50 =2,5 mol/L.
C) La solution commerciale contient environ 9% en masse d'hydroxyde de sodium. Vrai.
2,5 *40 = 100 g d'hydroxyde de sodium dans 1 L de déboucheur soit dans 1100 g de déboucheur ; 100 / 1100 ~0,09.
D) Le dosage peut être suivi par condutimétrie. Faux.
La conductivité
de la solution varie au cours du dosage, mais les solutions sont trop
concentrées, il faudrait les diluer au moins 10 fois pour effectuer un
suivi conductimétrique..
|

