|
|
E.
Locard est le médecin français créateur du premier laboratoire de
police scientifique à Lyon en 1910. Son ambition était de substituer la
preuve matérielle au seul témoignage humain par l'analyse systématique
des traces laissées par le coupable.
Parmi ces innombrables travaux, le principe dit "déchange de Locard" reste le plus célèbre :
" On ne peut aller et revenir d'un endroit, entrer et sortir d'une
pièce sans apporter et déposer quelque chose de soi, sans emporter et
prendre quelque chose qui se trouvait auparavant dans l'endroit ou la
pièce".
On peut donc espérer contribuer à établir la culpabilité ou l'innocence
d'un suspect en comparant divers éléments matériels prélevés sur ces
affaires et sur la scène du crime. parmi ces éléments il est fréquent
d'avoir à comparer des fragments de verre.
Sauf mention contraire, en fin de partie, on considèrera que la lumière
blanche se comporte comme une radiation monochromatique que l'on
identifiera à la lumière de la raie jaune du sodium de longueur d'onde l = 589,3 nm.
Généralités.
On considère un rayon lumineux incident se propageant dans le milieu 1, d'incce de réfraction n1. Il arrive avec un angle d'incidence i1, en I, sur la surface plane ( appelée dioptre ) séparant le milieu 1 du milieu 2, d'indice de réfraction n2. On notera i2 l'angle d'élergence du rayon lumineux.
La ligne en pointillés est la normale au dioptre. La ligne en tirets
est le prolongement dans le milieu 2 du rayon incident. Le sens positif
pour compter les angles est indiqué.
Reproduire le schéma en précisant bien les angles considérés et écrire la loi de Descartes de la réfraction.
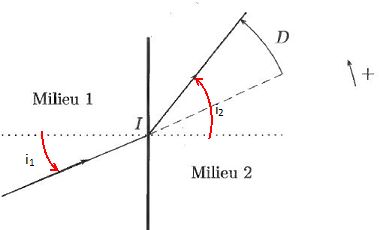
n1 sin i1 = n2 sin i2.
On appelle D la déviation du rayon lumineux. Exprimer D en fonction de i1 et i2.
D = i2-i1.
Calculet i2 et D dans les deux cas suivants :
n1 =1,50 ( verre); i1 = 30° et n2 =1,33 (eau).
sin i2 = 1,50 sin 30 / 1,33 =0,564 ; i2 = 34,3 ~34°; D = 34,3-30,0 = 4,3 °.
n1 =1,00 (air); i1 = 30° et n2 =1,50 (verre).
sin i2 = 1,00 sin 30 / 1,50 =0,333 ; i2 = 19,47 ~19°; D = 19-30 = -11°.
Que
remarque-t-on quand à la position du rayon réfracté par rapport à la
normale, quand on la compare à celle du rayon incident. Comment cela se
traduit-il sur D ? Proposer une formulation en français avec la consigne de ne pas utiliser le mot angle.
Si le milieu 2 est plus réfringent que le milieu 1( n2 > n1), le rayon réfracté est plus proche de la normale que le rayon incident. La déviation D est comptée négativement.
Si le milieu 2 est moins réfringent que le milieu 1( n2 < n1),
le rayon réfracté s'éloigne de la normale par rapport au rayon
incident. La déviation D est positive. Dans ce dernier cas, le rayon
émergent n'est pas toujours présent.
En
déduire qu'il existe une configuration dans laquelle il peut ne pas
exister de rayon réfracté. Exprimer l'angle d'incidence maximal à ne
pas dépasser en fonction de n1 et n2. le calculer dans le cas du verre et de l'eau.
sin i2 = n1/n2 sin i1 avec sin i2 inférieur ou égal à 1 et n1/n2 >1 ( milieu 1 plus réfringent que le milieu 2 ).
sin i1max =n2/n1 sin 90 =n2/n1.
sin i1max =1,33/1,50 =0,887 ; i1max =62,5°.
On parle dans ce cas de phénomène de réflexion totale : le rayon
incident est alors réfléchi et suit la loi de Descartes de la
réflexion. Rappeler cette loi et l'illustrer par un schéma.
Les rayons incident et réfléchi sont dans le même plan ; l'angle d'incidence et l'angle de réflexion ont la même valeur.
|
| .
. |
.
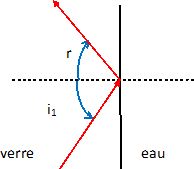
Le prisme.
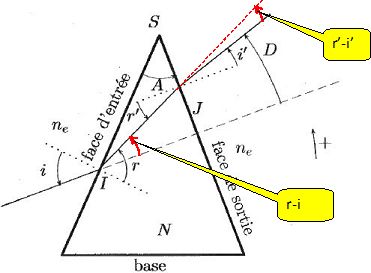
On considère un prisme d'angle au sommet A, fabrriqué dans un matériau
homogène d'indice de réfraction N. Il est entouré d'un milieu d'indice ne.
Les angles sont comptés positivement dans le sens trigonométrique. Un
rayon lumineux arrive en I sur la face dite d'entrée et émerge de la
face de sortie en J.
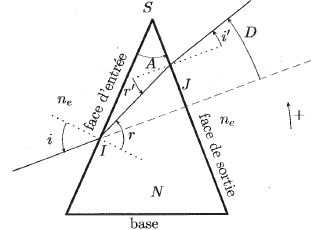
Ecrire les équations traduisant les réfractions en I et J.
En I : ne sin i = N sin r ; en J : N sin r' = ne sin i'.
En considérant le triangle SIJ, écrire une relation entre A, r et r'. Montrer que D = A+i'-i.
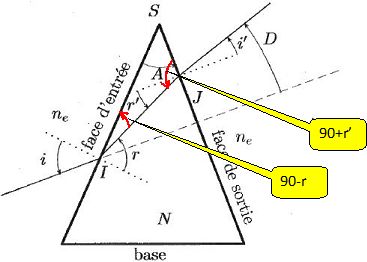
A+90-r +90+r' = 180 ; A = r-r'.
|
D = r-i -(r'-i') = -i+i'+A.
|
Les graphes suivants donnent ( pas nécessairement dans cet ordre ), dans le cas N=1,40 et ne = 1,20 d'une part et N=1,20 et ne
= 1,40 d'autre part, l'allure des graphes de la déviation D en fonction
de l'angle d'incidence D(i) pour diverses valeurs de l'angle A. Sur
chaque courbe la valeur numérique est celle de l'angle A exprimée en
degrés.
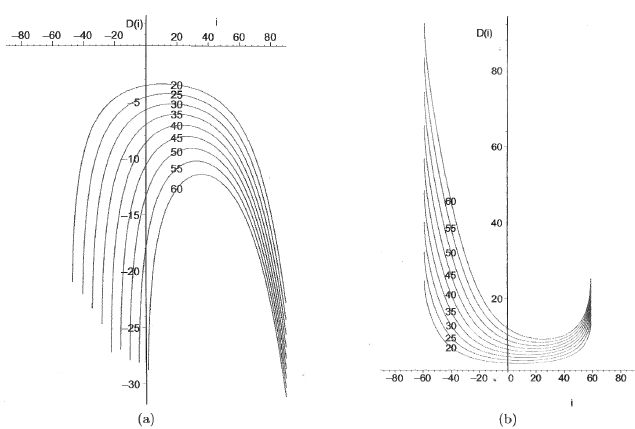
Précisez, en justifiant, quel graphe correspond à N>ne ?
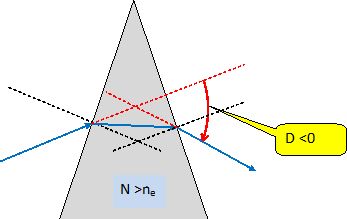Pour N>ne, la déviation est négative, donc schéma (a).
Qu'y-a-t-il
de remarquable quand au signe de D pour une configuration donnée ?
Formuler en français le comportement du rayon incident à la traversée
du prisme suivant que N>ne ou N < ne.
N>ne : D est négative : le rayon incident est dévié vers la base du prisme.
N < ne : D est positive : le rayon incident est dévié vers le sommet du prisme.
Préciser la dépendance de D avec l'angle A, toutes choses étant égales par ailleurs.
La déviation présente un extrémum pour une certaine valeur de i. En valeur absolue, la valeur de cet extrémum augmente avec A.
Les résultats précédents sont-ils encore valables si le sommet du prisme est tronqué et la base non rectiligne ? Sous condition, bien sûr, qu'après la première réfraction le rayon lumineux arrive sur la face de sortie.
Les résultats précédents restent valables : la réfraction ne fait intervenir que les faces d'entrée et de sortie non parallèles.
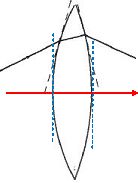
On a représenté le détail du trajet d'un rayon dans une lentille mince
dite à bords minces, entourée d'air. On fait apparaître les plans
tangents aux deux faces de la lentille aux deux points d'entrée et de
sortie du rayon lumineux.
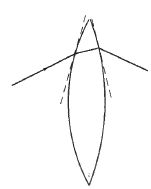
Justifier que cette lentille mince est convergente.
Cette
lentille peut être considérée comme deux prismes accolés par leur base.
L'indice du verre de la lentille étant supérieur à celui de l'air
entourant la lentille, les rayons incidents sont déviés, lors de sa
traversée,vers la base des prisme. La lentille est donc convergente.
Quel rayon incident n'est pas dévié à la traversée de la lentille ? Justifier.
Le rayon incident perpendiculaire aux faces d'entrée et de sortie n'est
pas dévié : l'angle d'incidence étant nul, sin i = 0 entraîne sin r = 0
soit r =0.
Définir ce qu'est le foyer principal image d'une lentille et justifier que la lentille puisse en posséder un.
Le foyer principal image est l'image d'un point objet situé à l'infini
sur l'axe optique principal. Un faisceau incident de rayons parallèles
entre eux et à l'axe optique émergent après traversée de la lentille en
passant par le foyer principal image. Pour ce faisceau parallèle, les
rayons plus éloignés de l'axe optique principal, possèdent un angle
d'incidence i de plus en plus grand : ils seront davantage déviés.
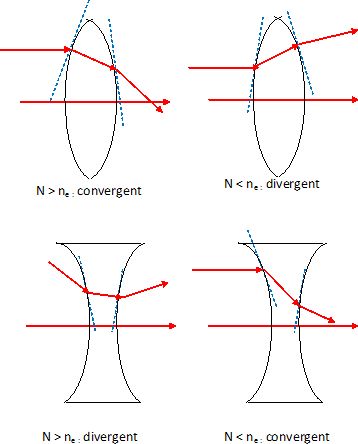
Préciser
la nature convergente ou divergente d'une lentille suivant qu'elle est
plus ou moins épaisse au centre, et suivant, qu'elle est entourée d'un
milieu d'indice plus faible ou plus grand que celui du verre dont elle
est constituée.
|