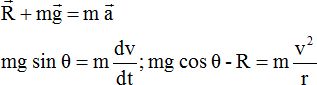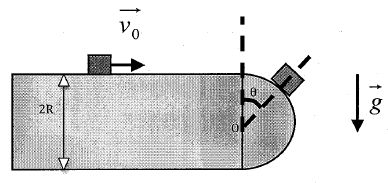
Mouvement d'un point matériel sur le bord d'une table : concours ITPE 2012. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

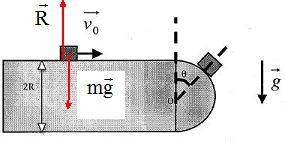
. La table est parfaitement lisse. Le mouvement de glissement du corps de masse m, lancé à la vitese initiale v0 est plan. Mouvement sur la partie horizontale. Les frottements étant négligeables, le corps est soumis à son poids et à l'action de la table. Représenter les forces qui s'exercent sur le système.. Quel est la nature du mouvement ? Quelle est la vitesse du système lorsqu'il aborde le bord de la table ? Les forces étant perpendiculaire à la vitesse ne travaillent pas et en conséquence, l'énergie cinétique, donc la valeur de la vitesse du système ne sont pas modifiées. Le mouvement est rectiligne uniforme. En arrivant au bord de la table la vitesse du système est v0. . . . . Mouvement sur le profil arrondi. Dessiner les forces qui s'exercent sur le système. 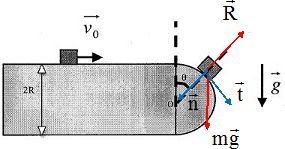Ecrire l'équation vectorielle du mouvement. 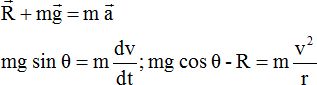Exprimer l'énergie mécanique du système. Quelle propriété présente cette énergie ? En absence de frottement et de force motrice, l'énergie mécanique du système reste constante. On choisit le point O comme référence de l'énergie potentielle de pesanteur. Energie mécanique initiale : ½mv02 + mg r. Energie mécanique à la date t : ½mv2 + mg r cos q. Conservation de l'énergie mécanique : ½mv02 + mg r = ½mv2 + mg r cos q. v2 = v02 +2gr(1- cos q). Exprimer R, réaction du support en fonction de q . R = mg cos q - mv2/r = mg cos q - mv02 / r -2mg(1- cos q). R =  mg (3cos q -2)- mv02 / r. Le système décolle de la table pour q = p/6. Calculer v0. R = 0 au moment du décollage : v02  = g r(3cos( p/6) -2)= 0,6 g r ; v0 = (0,6 g r) ½.

menu