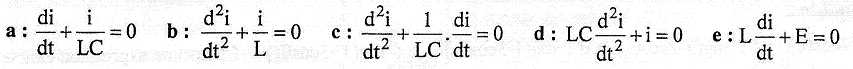|
|
On réalise un
circuit comprenant un générateur idéal de tension de fem E, un
interrupteur, un conducteur ohmique R, une bobine d'inductance L et de
résistance interne r. A un instant pris comme origine des dates, on
ferme le circuit et à l'aide d'un système informatisé, on visualise les
variations de la tension ubob aux bornes de la
bobine au cours du temps. R = 5 ohms ; L = 100 mH.
Calculer
l'énergie stockée dans la bobine ( mJ) lorsque le régime permanent est
atteint.
(10 ; 25 ; 35 ; 40 ; 50 ; autre ).
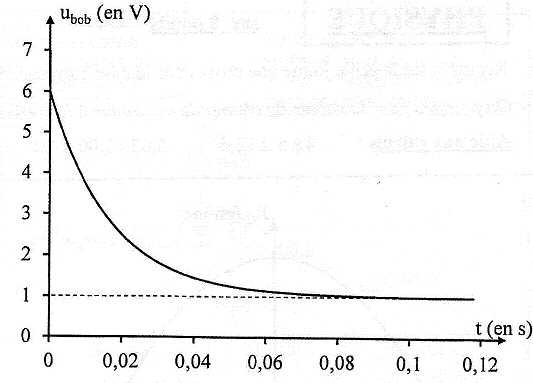
En régime permanent, ubob = rI = 1,0 V ( lecture
graphe) ; uR = RI ;
Additivité des tensions : E = rI +R I = 1 +R I = 1+5 I.
I = (E-1) / 5 =0,2 E -0,2.
A l'instant initial l'intensité est nulle et E =ubob =
6,0 V ( lecture graphe ).
I = 0,2*6 -0,2 = 1,0 A.
Energie stockée en régime permanent : ½LI2 =
0,5*0,10 *12 =0,05 J = 50
mJ.
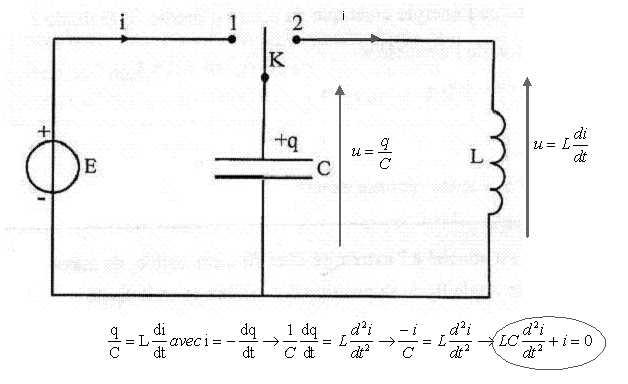
L'interrupteur
est en position 1 pendant le temps nécessaire pour que le condensateur
se charge complètement. On le bascule ensuite en position 2. Le circuit
est alors le siège d'oscillations électriques non amorties.
Parmi les équations différenteilles suivantes relatives à l'intensité, laquelle
est exacte ?
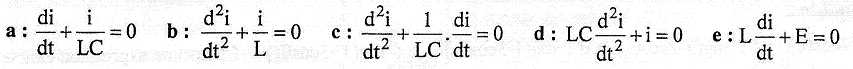
|
| .
. |
.
Le
réacteur d'une centrale nucléaire fonctionne en uranium enrichi. Par
capture d'un neutron lent, le noyau 23592U
subit la réaction suivante :
23592U +10n
---> 14857La +85xBr
+y10n.
Combien y a t-il de propositions exactes ?
A) x = 35 ; y = 2. Faux.
Conservation de la
charge : 92 = 57 + x ; x = 35 ; conservation du nombre de nucléons :
235+1 = 148 +85 + y : y = 3.
B) Cette
réaction de fission est spontanée et exoénergétique. Faux.
Cette réaction de
fission est provoquée par un neutron.
C) La perte de masse est égale à : |Dm|= m(23592U)-m(14857La)
- m(85xBr) -3 m(10n). Faux
|Dm|= m(23592U)-m(14857La)
- m(85xBr) -2 m(10n)
D) La perte de masse peut s'exprimer
en MeV c2. Faux.
|Dm| = DE/c2 s'exprime em MeV/ c2.
E) Le noyau d'uranium 235 est dit fissile. Vrai.
|
Une lampe à UV
peut être utilisée pour stériliser des instruments chirurgicaux. Chaque
photon émis par cette lampe a une énergie voisine de 4,89 eV.
h = 6,63 10-34 J s ; 1 eV = 1,602 10-19
J ; c = 3,00 108 m/s ; 6,63 *3 ~20 ; 4,89 *1,602
~8.
Calculer la longueur d'onde l ( en µm) du
rayonnement émis.
(0,16
; 0,25 ; 0,40 ; 2,5 ; 4,0 ; autre ).
E
= hc/l ; l = hc/E =6,63
10-34*3,00 108 /(4,89 *1,602
10-19 ) ~20 10-26 / (8 10-19)
~20 / 8 10-7 ~2,5 10-7 m ~0,25
µm.
|
|