|
.
|
|
Bobine et
condensateur.
Dans un circuit électrique comportant une bobine :
A) l'énergie stockée dans la bobine ne subit pas de discontinuité. ( vrai
).
B) l'intensité du courant dans la bobine ne subit pas de discontinuité.
( vrai ).
C) la tension aux
bornes de la bobine ne subit pas de discontinuité ( faux ).
u = Ldi/dt + ri.
D) l'énergie stockée dans la bobine dépend de la résistance de la
bobine (faux ).
E) aucune bonne réponse.
Dans un circuit
électrique comportant un condensateur :
A) l'énergie stockée dans le condensateur ne subit pas de
discontinuité. ( vrai
).
B) l'intensité du courant dans la branche comportant le condensateur ne
subit pas de discontinuité. ( faux ).
C) la tension aux
bornes du condensateur ne subit pas de discontinuité ( vrai ).
D) la charge portée par les armatures du condensateur ne subit
pas de discontinuité ( vrai ).
E) aucune bonne réponse.
Le circuit d'accord d'un récepteur
radio comporte un circuit oscillant constiyué d'une bobine et d'un
condensateur. l'inductance L vaut 0,1 µH lorsque la fréquence
propre vaut 89,9 MHz. La capacité du condensateur vaut : (
en F)
3 10-11 ; 3 10-8
; 3 10-5
; 3 10-3
; aucune bonne réponse.
f = 1 /(2p(LC)½ ; C = 1 /(f2
4 p2
L) =1 / ((89,9 106)2*4*3,142
*10-7) ~3 10-11 F.
|
| .
. |
Détermination
de la masse volumique d'un fluide.
Une sphère en acier ( r =
7,80 g cm-3) de rayon r = 1,20 cm est suspendue à
l'extrémité d'un ressort vertical de longueur à vide L0 =
10,0 cm. La longueur du ressort à l'équilibre vaut L1 = 13,5
cm.
Sans modifier le dispositif précédent, la sphère est ensuite immergée
dans un fluide dont on souhaite déterminer la masse volumique. Quand la
sphère immergée est immobile, la longueur du ressort vaut L2
= 12,5 cm.
Lorsque la sphère immergée dans le fluide est à l'équilibre, elle est
soumise à :
A) une force. (faux).
B) deux forces. ( faux ). C) trois forces ( vrai ). D) quatre forces
( faux ). E) Aucune bonne réponse
La sphère immergée est soumise
à son poids, à la poussée d'Archimède et à la tension du ressort.
La constante de raideur du ressort
vaut ( N / m) :
1,58
; 15,8 ; 158 ; 1,58 103 ; aucune bonne réponse.
La sphère non
immergée est soumise à son poids et à la tension du ressort ; ces deux
forces opposées ont même valeur.
mg = k(L1-L0 ); m = 4/3 p r3 r =4/3*3,14*1,203 *
7,80 =56,46 g. k = 56,46 10-3
*9,81 / (0,135-0,100) =15,825 ~15,8 N m-1.
La masse volumique du
fluide vaut ( g cm-3).
Poussée d'Archimède : 4/3 p r3 rfluide g ; poids
apparent = poids - poussée = 4/3 p
r3g(r-rfluide) = 4/3*3,14*1,203*9,81 (r-rfluide)
= 71,0 (r-rfluide), exprimée en mN.
poids apparent = tension du ressort = k(L3-L0)
=15,825 ( 0,125-0,100) =0,395 625 N = 395,625 mN.
395,625 = 71,0(r-rfluide) ;
r-rfluide = 395,625 /
71,0 = 5,572 ; rfluide
=7,80-5,572 =2,2278 ~2,23 g cm-3.
Dans
la position d'équilibre, l'accélération du pendule possède les mêmes
caractéristiques que dans le cas d'un mouvement uniforme. Lors du
premier passage dans la position d'équilibre :
A) La tension du fil a pour valeur 0,64 N. ( faux ).
-mg + T = mv2/L
; T = mg +mv2/L =0,075
(9,8 +12/0,80 )~0,83 N.
B)
La tension du fil a pour valeur 0,74 N. ( faux ).
C)
La tension du fil a pour valeur 0,83 N. ( vrai ).
D) La tension dépend de v0. ( vrai ).
La vitesse au passage de la
position d'équilibre dépend de v0.
E) Aucune bonne réponse. ( faux ).
Génératrice
d'un circuit électrique.
La génératrice est un générateur de tension continu qui convertit
l'énergie mécanique en énergie électrique. Une génératrice alimente un
moteur électrique. La tension aux bornes de la génératrice vaut U =
80,0 V et l'intensité du courant circulant dans le circuit vaut I =
6,50 A. Le travail reçu par la génératrice en une heure est 3,23 MJ.
Le transfert thermique réalisé pendant cette durée par la génératrice
dans l'environnement est :
520 J ; 32,1 kJ ; 1,87 103 kJ ; 1,36 103 kJ ;
aucune bonne réponse.
Puissance électrique disponible
: UI = 80,0 * 6,50 =520 W. Puissance reçue : 3,23 106 / 3600
=897,2 W
Puissance thermique : 897,2-520
= =377,2 W ; transfert
thermique 377,2 *3600 =1,36 106
J = 1,36 103 kJ.
La résistance interne de la génératrice vaut :
21, 2 mW ; 200 mW ; 2,12 W ;12,3 W ; aucune bonne réponse.
Puissance thermique rI2
; r =377,2 /
(6,502) = 8,92
W.
Le rendement énergétique de la génératrice est :
42 % ; 50 % ;
68 % ; 75 % ; aucune bonne réponse.
520 / 897,2~0,58
( 58 %).
La résistance interne du moteur est r'=2,80 ohms. Le travail fourni par
le moteur en une heure est :
426 kJ ; 932 kJ ; 1,45 103 kJ ; 2,80 103 kJ ;
aucune bonne réponse.
Tension aux bornes du moteur U
= E' +r'I ; E' = U-r'I = 80,0 -2,80*6,50 =61,8 V
Travail mécanique : E' I t =
61,8 *6,50 *3600 =1,45 106 J = 1,45
103 kJ.
Le transfert thermique réalisé par le moteur dans l'environnement est :
426 kJ ; 932 kJ ; 1,45 103 kJ ; 2,80 103 kJ ;
aucune bonne réponse.
r'I2t
= 2,80*6,502*3600 =4,26 105 J = 426
kJ.
|
Association de
résistances.
R1 =10,0 ohms ; R2 = 2R1 ; R3
= 3 R1 ; R4 = 4 R1.
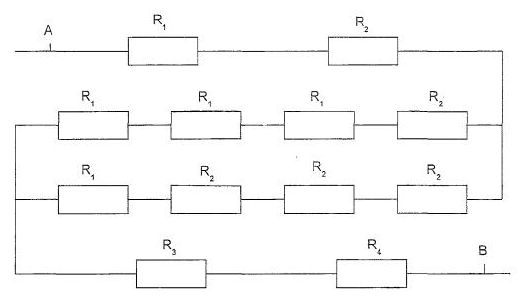
La résistance équivalente au dipole AB vaut (en ohms) : 100 ; 150 ; 180
; 220 ; aucune bonne réponse.
R1,
R1, R1, R2, en série équivalent à R5
=5 R1 = 50 ohms.
R1,
R2, R2, R2, en série équivalent à R7
=7 R1 = 70 ohms.
R5,
R7 en dérivation équivalent à : R6
= R5 R7 / (R5+R7)
=50*70/120 =29,16 ohms.
R1,
R2, R6, R3, R4
en série équivalent
à R =R1 + R2 + R6 + R3 + R4
=10+20+29,16 +30+40
=129,1 ~129 ohms.
Ce dipole est
relié à une pile de résistance interne r = 3,0 ohms et de fem E = 9,0
V. L'intensité du courant qui parcourt le circuit est : ( en mA) 87 ;
68 ; 59 ; 40 ; aucune bonne réponse.
I = E /(r+R) =9 /
(3+129,1 )=0,0681 A = 68
mA.
L'énergie
dissipée dans le dipole AB par
effet joule pendant une minute est : 36 MJ ; 36 kJ ; 36 J ; 36
mJ; aucune bonne réponse.
RI2
t = 129,1 *0,06812 *60 ~36
J.
|
|
