|
|
On
numérise un signal sonore.
Comment
distingue-t-on le signal numérique du signal analogique sur
l'enregistrement ci-dessous ?
Signal analogique
: la courbe est continue, tous les valeurs sont possibles.
Signal numérique : la courbe est un ensemble de fonctions constantes
par intervalle, seules quelques valeurs sont possibles.
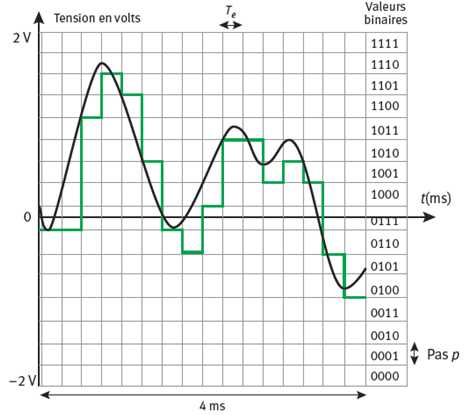
Que vaut
le nombre n de bits de la carte d'acquisition utilisée ?
16 = 24
valeurs numériques sont possibles : n = 4 bits.
Les tensions minimale et maximales mesurables sont -Um
et +Um.
Quelle
est la valeur de Um ?
Um = 2 V.
Soit n la valeur décimale du nombre binaire le plus grand du
convertisseur analogique numérique.
Quelle est
la valeur de n pour le binaire 1111 ?
n = 23 + 22 +21
+20 = 15.
Etablir la
relation entre Um, n et le
pas p de la numérisation. Calculer p.
Um -(-Um ) 4 V ; 2n
= 16 valeurs numériques possibles ; p = 2 Um / 2n
= 4/16 = 0,25 V.
Comment
varierait le pas p de l'acquisition si le nombre de bits du CAN était
plus important ?
A Um constante, si n croît alors 2n
augmente et le pas diminue. La conversion sera plus précise, la
numérisation du son sera plus fidèle.
Déterminer
la fréquence d'échantillonnage.
1/Te = 103 Hz.
On augmente la fréquence d'échantillonnage.
Quels
inconvénient ces choix impliquent-ils du point de vue du stockage de
l'enregistrement ?
Il faudra stocker un très grand nombre de bits, mais le signal numérisé
sera très ressemblant au signal analogique.
|
| .
. |
.
|
Etude
du Convertisseur Analogique Numérique.
On notera [N] la valeur binaire du mot numérique de sortie du CAN et [N]10
sa valeur décimale.
La caractéristique de transfert du CAN, [N]10 =
f(u3) se présente comme une succession de
paliers s'appuyant sur une droite D comme le montre la figure :
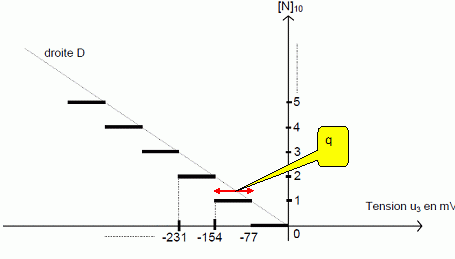
Quel est
l’intérêt d’avoir un nombre de bits important ?
La résolution ou variation de la tension d'entrée donnant
lieu à une variation
d' une unité de la donnée numérique présente en sortie, est bien
meilleure.
Calculer
le nombre de combinaisons possibles pour [N].
Il existe 28 combinaisons de sortie possibles
soit : 28= 256.
Déterminer
[NMAX] et [NMAX]10.
La première combinaison
correspond à zéro ; la plus grande correspond à [NMAX]
=255 " en décimal".
255 = 1*27 + 1*26 + 1*25
+ 1*24 + 1*23 + 1*22
+ 1*21 + 1*20 ;
55 sécrit : 1111 1111 en binaire et FF en hexadécimal.
[NMAX]10
= [NMAX] *q
= 255 *(-0,077) ~ -19,6 V.
En pratique on ne peut pas dépasser la tension de saturation du CAN ( -Vsat
= -15 V)
et dans ce cas [NMAX] =15 / 0,077=195 .
Déterminer
la valeur du quantum q.
q =217-154 = 154 -77 = 77 mV.
|
|
Pour
numériser la tension u4 issue de
l'amplificateur, on emploie un CAN. On notera N la valeur décimale du
mot numérique codé en binaire naturel.
On considère que l'afficheur placé à la suite du
CAN indique sur 3 digits (avec point décimal fixe) la valeur de N comme
le montre l'exemple suivant :
Pour N = 125, l'afficheur indique 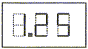 Ce qui correspond à une hauteur H de 1,25 mètre
dans le bac. Ce qui correspond à une hauteur H de 1,25 mètre
dans le bac.
- Sachant que
l'afficheur peut indiquer jusqu'à une hauteur de 2 mètres, montrer
qu'un CAN 8 bits convient pour ce système.
- Le
début de la caractéristique de transfert N = f(u4) du convertisseur
est représentée ci-dessous :
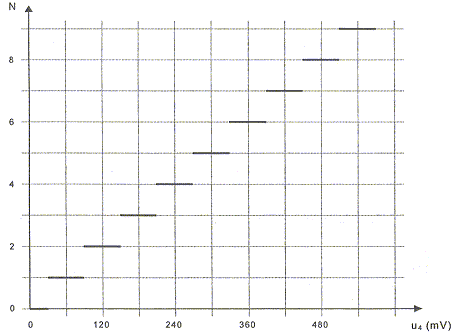
-
Déterminer le quantum q.
- Déterminer, pour une tension u4
de 4,5 V, le nombre N correspondant. En déduire l'indication de
l'afficheur.
Un CAN 8 bits convient pour ce système :
Une hauteur h
= 2 m correspond à une valeur de N égale à 200.
Or un CAN 8
bits permet d'obtenir 256 valeurs analogiques.
256 étant
supérieure à 200, un CAN 8 bits convient.
Le quantum q :
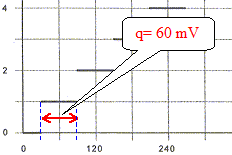
Pour une
tension u4 de 4,5 V, le nombre N correspondant :
N= u4/q
= 4,5 / 0,06 ; N= 75.
L'afficheur
indique h = 0,75 m.
|
|