|
|
L’instant
tant attendu par l’étudiant est arrivé. Le voilà en avion à 4000 m
d’altitude et il se prépare à sauter.
A cette altitude, la pression atmosphérique patm est égale à 5,1 104 Pa.
Donner
la relation liant la pression p et la valeur F de la force
pressante s’exerçant perpendiculairement à une surface d’aire S.
Indiquer les unités des différentes grandeurs dans le système
international.
F = p S avec p en pascal, F en newton et S en m2.
Calculer la valeur F de la force exercée par l’air sur la surface
S du hublot de l’avion.
Donnée : 1cm2 = 1 10-4 m2 ; S = 900 cm².
F = 900 10-4 *5,1 104 =4590 ~4,6 103 N.
Le grand saut.
Le système {étudiant – parachute} a une masse m égale à 80 kg.
L’étudiant quitte l’avion au point A avec une vitesse initiale vA nulle
pour effectuer une chute verticale de hauteur AB avant l’ouverture du
parachute.
On supposera que le système est en chute libre. Il n’est donc soumis
qu’à son poids.
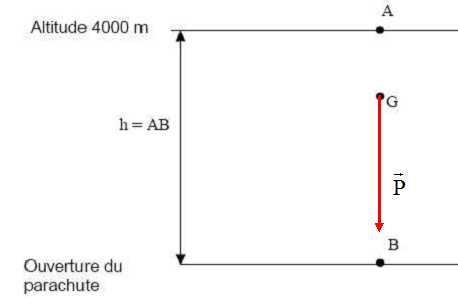
Donner les caractéristiques (direction, sens, norme) du vecteur
poids P du système. Représenter au point G, le vecteur poids P.
Données : P = m.g ; g = 9,8 N.kg-1. Echelle 1 cm pour 200 N.
P = 80*9,8 =784 ~7,9 102 N. (flèche de 4 cm ).
Direction verticale ; sen : vers le bas ; appliqué au centre d'inertie G; norme P = mg.
Donner la relation liant le travail du poids W (P) AB et la hauteur h = AB.
Le travail du poids est moteur en descente : W(P)AB = mg h.
Montrer
que la valeur W (P) AB est voisine de 3,9 x 105 S.I. pour une hauteur de chute h = AB = 500 m. Nommer l’unité du travail.
W(P)AB = mg h= 80*9,8 *500 =3,92 105 ~3,9 105 joules ( J).
|
.
|
Calcul
de la vitesse du système au point B.
L’expression littérale de l’énergie cinétique d’un système de masse
m et de vitesse v en translation est donnée par la relation :
Ec =½mv2.
Donner l’unité de l’énergie cinétique dans le système international
(S.I). Calculer l’énergie cinétique Ec(A) du système au point A.
L'énergie cinétique s'exprime en joule. La vitesse en A étant nulle, l'énergie cinétique est nulle au point A.
En appliquant le théorème de l’énergie cinétique entre les points
A et B, déduire la valeur de l’énergie cinétique au point B.
Ec(B)-Ec(A) = mgh ; Ec(B)-0 = mgh ; Ec(B) = mgh = 3,9 105 J.
Montrer que la vitesse vB du système au point B est égale à 99
m.s-1 (ce qui correspond à une vitesse de 356 km.h-1).
Ec(B) =½mvB2; vB2 =2
Ec(B) / m ; vB = (2
Ec(B) / m)½ = (2*3,92 105 / 80)½ = 99 m/s.
En B, l’étudiant ouvre son parachute. En arrivant au sol la
vitesse du système est voisine de 20 km.h-1.
Quel est l’intérêt du parachute ?
Le parachute permet de ralentir le système et d'arriver au sol avec une vitesse sufisamment faible. |
|