Pharmacocinétique : mode d'action d'un médicament, Capes 2014. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . La pharmacocinétique est l'étude du devenir d'un médicament dans l'organisme. Après son administration, le prinipe actif franchit différentes barrières pour finalement accéder au plasma sanguin. La circulation sanguine assure sa distribution dans l'organisme. Il peut alors parvenir  à son site d'action, ou être métabolisé ( c'est à dire transformé ) puis éliminé ou encore être stocké. Sa concentration dans le plasma sanguin évolue donc au cours du temps. Conditions de passage transmembranaire par diffusion. L'organisme humain est assimilé à plusieurs compartiments aqueux séparés entre eux par des membranes cellulaires lipidiques qu'un médicament doit traverser pour passer d'un compartiment à un autre ( par exemple pour passer du plasma sanguin au liquide intracellulaire ). On donne une représentation schématique d'une telle membrane lipidique. 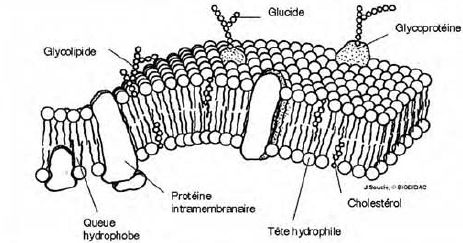Source : http://www.defl.ca/~debloisj_dev/cellules/contenu/cellule2.html 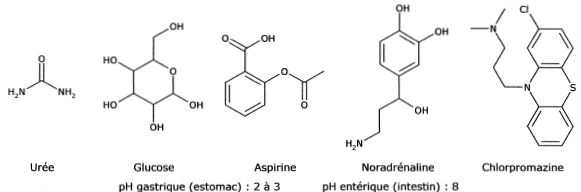Proposer une justification précise et concise pour chacune des trois observations suivantes. ( un seul argument est attendu par observation ) L'urée traverse trois fois plus vite une membrane cellulaire que le glucose : l'urée est une molécule de très petite taille par rapport au glucose. La noradrénaline traverse beaucoup moins vite la membrane cellulaire que la chlorpromazine : la noradrénaline beaucoup plus polaire que la chlorpromazine, se fixe sur les têtes hydrophiles de la membrane lipidique. L'aspirine ingérée par voie orale est rapidement absorbée au niveau de l'estomac mais plus lentement au niveau de l'intestin : dans l'estomac ( pH ~ 3 ) c'est la forme acide AH de l'aspirine qui prédomine, alors que dans l'intestin ( pH ~8 ) c'est la forme A- ( base conjuguée de AH) qui prédomine.   Etude de modèles utilisés en pharmacocinétique. Après administration d'un médicament, la mesure de sa concentration dans le plasma sanguin est en général possible, ce qui permet de suivre son évolution au cours du temps. Cette évolution a été suivie pour l'acide valproïque, médicament antiépileptique commercialisé sous le nom de Dékapine. Le graphe suivant donne l'évolution temporelle de la concentration massique C de cette molécule dans le plasma sanguin d'un patient à qui on a administré une masse D = 2,0 g d'acide valproïque ( appelé dose ) de deux manières différentes : injection intraveineuse (a) et administration par voie orale d'une forme galénique dite à "libération prolongée" (b). 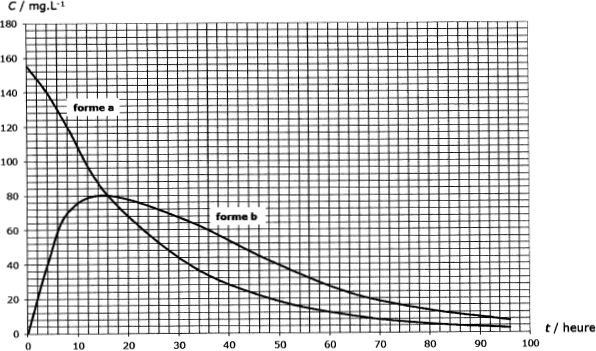Les taux thérapeutiques recommandées sont de 40 à 100 mg/L. Commenter et comparer les deux modes d'administration. Par voie intraveineuse, ( le taux initial est bien trop grand par rapport à ceux recommandés), la concentration dans le plasma décroît assez rapidementde manière quasiment exponentielle. Le taux devient inférieur à 40 mg/L au bout de 30 heures. Par voie orale, la concentration dans le plasma atteint 40 mg/L au bout de 4 h, puis un maximum ( 80 mg/L) au bout de 12 h et enfin décroît plus lentement que dans le cas (a). ( le taux devient inférieur à 40 mg/L) au bout de 50 h ). La libération prolongée augmente la durée d'action de ce médicament. . Modèle pour l'administration intraveineuse ( I.V). La dose est directement injectée dans le plasma sanguin à la date t=0. La consommation du médicament par l'organisme est modèlisée par une loi cinétique d'ordre 1, de constante de vitesse ke. On note C la concentration massique d'acide valproïque dans le plasma à la date t et C0 la concentration massique initiale de cet acide. Déterminer l'expression de C à la date t. dC/dt = -ke C ; dC / C = -kedt ; ln C = -ket + Cste ; ln (C/C0) = -ket ou C = C0 exp(-ket). Exploiter numériquement les résultats du tableau suivant. Déterminer ke et C0. 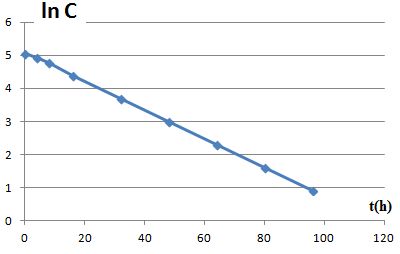temps t (h) 0,08 4,0 8,0 16,0 32,0 48,0 64,0 80,0 96,0 C ( mg/L) 155 140 120 80 40 20 10 5,0 2,5 ln C 5,04 4,94 4,79 4,38 3,69 3,00 2,30 1,61 0,916 ln C = -0,0435 t + 5,09 avec t en heure ; de plus ln C = - ket + ln C0 ; par identification : ke = 0,0435 h-1 ; C0 = 162 mg L-1. Lorsque la dose est administrée à la date t=0, elle est dissoute dans une partie de l'organisme que l'on assimile à une solution de volume V0 appelé volume de distribution. Déduire V0 des résultats. On a administré une masse D = 2,0 g d'acide valproïque : V0 =D / C0 = 2 / 0,162 ~12 L. 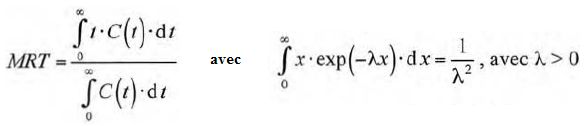Le temps de présence moyen d'un médicament dans le plasma sanguin ( noté MRT ) est défini par : Exprimer le MRT pour l'acide valproïque en fonction de ke puis le calculer. 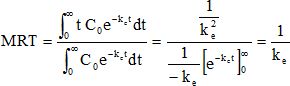MRT = 1 / 0,0435 ~23 h. Modèle pour l'administration par voie orale. La dose d'acide volproïque, de masse D, administrée par voie orale doit parvenir dans le plasma sanguin par échanges tout au long du tube digestif ( au niveau de l'estomac et de l'intestion en particulier ). L'absorption et la consommation par l'organisme du médicament sont modélisées par les lois cinétiques d'ordre 1 et de constantes de vitesse respectives ka et ke. On note respectivement mT(t) et mP(t) les masses d'acide valproïque dans le tube digestif et dans le plasma sanguin. 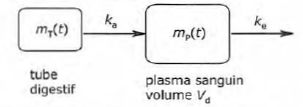Etablir le système d'équation différentielle vérifiée par mT(t) et mP(t). dmT(t) / dt = -ka mT(t) ; dmP(t) / dt = -ke mP(t) + ka mT(t) Donner l'expression de la masse mT. dmT(t) /  mT(t)  =  -kadt  ; ln mT(t) = -ka t + Cste ; ln mT(t=0) =ln D = Cste ; ln (mT(t) / D)= -ka t  ; mT(t) = D exp(-ka t). La résolution du système d'équations différentielles donne : mP(t) = ka/(ka-ke)D[ exp(-ket) -exp(-kat)]. En déduire l'expression de C(t), concentration dans le plasma sanguin. Introduire le volume de distribution Vd supposé identique à V0. C(t) = mP(t) / Vd =ka/(ka-ke)D / Vd[ exp(-ket) -exp(-kat)] Montrer que C(t) passe par un maximum noté Cmax à une date donnée tmax. Exprimer tmax en fonction de ke et ka. A tmax,dC/dt = 0 ; ke exp(-ketmax) = ka exp(-katmax) ; ln ke-ketmax = ln ka-katmax  ; tmax = ln (ke/ ka) /(ke-ka). A t = 0 et à t infini, C(t) =0, il s'agit donc bien d'un maximum. Montrer que Cmax = D/Vd exp(-ketmax). Cmax = ka/(ka-ke)D / Vd[ exp(-ketmax) -exp(-katmax)] =ka/(ka-ke)D / Vd[exp(-ketmax) (1-ke/ka)]=D / Vdexp(-ketmax). Evaluer graphiquement tmax et Cmax. Cmax = 80 mg / L et tmax ~15 h. En déduire une évaluation des valeurs de ka et ke. Cmax = D/Vd exp(-ketmax) ; 0,08 = 2,0 / 12 exp(-15ke) ; 0,48 = exp(-15ke) ; ke = -ln 0,48 / 15 =0,04893 ~0,049 h-1. C(t) = mP(t) / Vd =ka/(ka-ke)D / Vd[ exp(-ket) -exp(-kat)] et les valeurs de la courbe b conduitsent à : ka ~0,07 h-1. Avec ce modèle, le MRT s'exprime par : MRT = 1/ke + 1/ ka. Calculer ce MRT, comparer à celui de la forme (a) et conclure. MRT = 1/0,049 +1/0,07 =34 heures. La libération du médicament est prolongée, ce qui augmente la durée d'action de ce médicament.

menu