|
|
|
|
On considère un
réseau cubique centré CC de paramètre de maille a constitué d'un seul
type d'atomes de rayon R. Le fer alpha cristallise dans ce type de
réseau. En supposant que l'on a contact entre atomes :
Faire
un schéma de la structure.
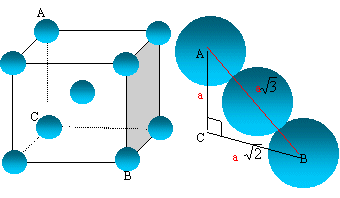
La tangence
s'effectue suivant la grande diagonale du cube :
"a" racine carrée
(3) = 4 R ; R/a = 3½/4.
Déterminer
le nombre d'atomes par maille.
Les atomes des
sommets apartiennent à 8 mailles et comptent pour 1/8 ; 1 atome central
:
8(1/8)+1 = 2.
Exprimer
la compacité indépendamment de R et a.
La
compacité C, comprise entre
0 et 1, mesure le taux d'occupation de l'espace par les atomes ou les
ions assimilés à des sphères. C= volume occupé / volume de la maille.
volume
occupé : 2*(4/3pR3) ; volume de la
maille : a3 et R/a
= racine carrée
(3) /4= 0,433.
C = 8/3 p
*0,4333 =0,68.
Calculer
la coordinence.
La
coordinence est le nombre de
plus proches voisins d'une sphère quelconque, ces voisins étant
tangents à la sphère envisagée. Chaque atome de fer alpha est au centre
d'un cube, entouré de 8 autres atomes : coordinence
= 8.
Calculer
la masse r
volumique du fer alpha.
M(Fe)
= 55,8 g/mol ; a =2,866 angstrôms = 2,866 10-10
m.
La masse volumique m (kg m-3) est la masse
d'une maille (kg) divisée par le volume de la maille (m3)
masse d'une maille : masse de deux atomes de fer = 2*masse molaire (kg)
/nombre d'avogadro
soit 2*55,8 10-3 / 6,023 1023
= 1,853 10-25 kg
volume d'une maille a3 = (2,866 10-10)3=
2,354 10-29 m3.
r =
1,853 10-25 /3,254 10-29 =7,87
103 kg m-3.
|
.
On mesure les variations de concentration en peroxyde d'hydrogène au cours de la réaction de décomposition de l'eau oxygénée.
H2O2 --> H2O + ½O2(g).
| temps (min) | 0 | 30 | 60 | 90 | 120 | 150 | 180 | | [H2O2] mol/L | 0,334 | 0,264 | 0,210 | 0,166 | 0,132 | 0,104 | 0,083 | | ln ( [H2O2] / [H2O2]0) | 0 | ln(0,264 / 0,334) =-0,235 | ln(0,210 / 0,334)=-0,464 | -0,700 | -0,928 | -1,17 | -1,39 | | k =-ln ( [H2O2] / [H2O2]0) / t | xxxx | 0,235 / 30 = 7,83 10-3 min-1 | 0,464 /60 =7,73 10-3 min-1 | 7,78 10-3 | 7,73 10-3 | 7,80 10-3 | 7,72 10-3 |
Vérifier que l'ordre global de cette réaction est de 1.
Dans l'hypothèse d'un ordre global de 1, on trace le graphe ln ( [H2O2] / [H2O2]0) = f(t). Si on obtient une droite de coeffficient directeur -k, cette hypothèse est confirmée. 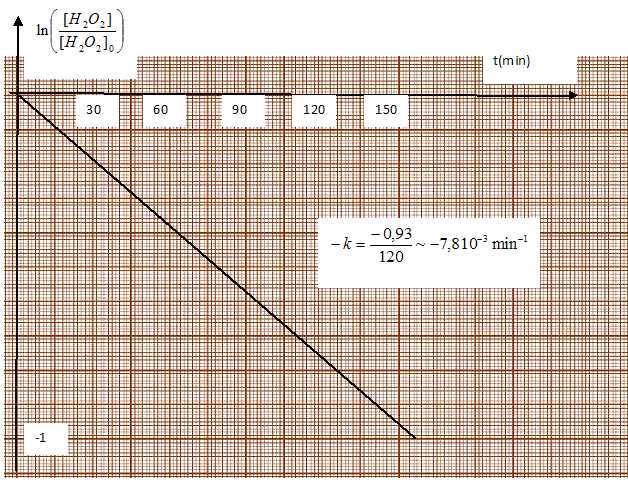
Calculer la constante de vitesse k et donner son unité.
Le graphe et la dernière ligne du tableau conduisent à k = 7,8 10-3 min-1.
Déterminer le temps de demi-réaction t½.
Dans le cas d'un ordre global égal à 1, le temps de demi-réaction vaut :
t½ = ln2 / k =ln2 / (7,8 10-3) ~90 min.
|
.
|

